Subgrid modeling is now widely used in the calculation of atmospheric processes and phenomena at large settlement areas. Grid spacing at the subgrid modeling can reach 300 km. Among the most popular models of subgrid model acquired Joseph Smagorinsky. This article examines the Smagorinsky model for an isothermal environment.
Subgrid modeling is characterized by a kind of subgrid scale D. The most common definition of subgrid scale dimensions for rectangular cells Dx, Dy, Dz at a moderate anisotropy of the grid as follows:
![]() (1)
(1)
and for strong anisotropy of grid as follows:
![]() (2)
(2)
Turbulent air flow occurring at subsonic speeds, in accordance with the «hypoacoustic» Boussinesq approximation can be described by the Navier-Stokes equations consisting of equations of motion and continuity for an incompressible viscous fluid:
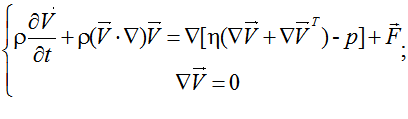 (3)
(3)
Here ![]() is velocity vector;
is velocity vector;
h is dynamic viscosity, Pa∙s; р is piezometric pressure, Pa; ![]() is specific force field, N per cubic m; p is air density, kg per cubic m.
is specific force field, N per cubic m; p is air density, kg per cubic m.
The system (1) is applicable for finding eddies of various scales in its analytical solution, but it is an unsolved mathematical problem. Among the numerical methods for the solution is the most accurate direct numerical simulation (DNS) – the solution of unsteady Navier-Stokes equations with a small time step on the dense grid , but it is now possible computing still do not allow the DNS to the large settlement areas. Therefore , in practice, often authors suggest solving Reynolds averaged in the system (2) the equation of motion (RANS):
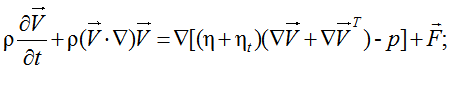 (4)
(4)
There ht is dynamic coefficient of turbulent viscosity, Pa∙s, ht = rkхуz; kхуz is eddy viscosity in different directions, m2
per s, for an anisotropic medium is given by the matrix 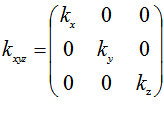 .
.
The coefficients of turbulent viscosity in subgrid Smagorinsky model defined by the system:
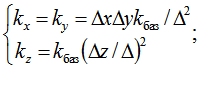 (5)
(5)
Here kбаз – is basic coefficient of turbulent viscosity, and contempt of the temperature gradient low altitude and temperature of the discharged impurities determined the approximate equation:
![]() ; (6)
; (6)
Here kф is background coefficient of turbulent viscosity, kф = 1-15 м2/с; ε = 0,1-0,4; Def (x; y; z) is function of
deformation or dissipation defined by the equation:
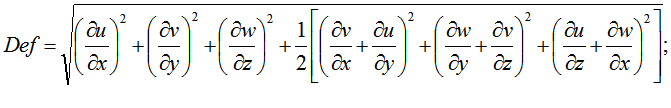
Most software packages such as Ansys CFX, Fluent, Flow Vision for the calculation for anisotropic media digested TBE on sub-elements within each of which can be regarded as an isotropic medium (Figure 1). To simplify the calculation of turbulent flow structure, the present author proposed a model to produce isotropization subgrid of turbulent viscosity determined by Smagorinsky model for an isothermal environment.
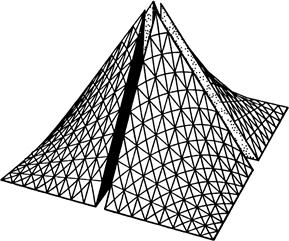
Figure 1 – Example of splitting finite element on the sub-elements [1]
The radical product DхDуDz in definition (1) can be interpreted as the volume of the rectangular cell, equal to the amount that would be occupied with the cubic cell edge D. In practice, the most common use is not rectangular and tetrahedral cells. Scale D cells form a regular tetrahedron volume Ω, by analogy with definition (1) can be found as:
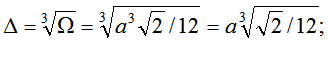 (7)
(7)
Here а is edge of tetrahedral cell.
Then coefficients of turbulent viscosity for grid with small anisotropy will be determined as:
![]() (8)
(8)
For computational domains with real geometry to build isotropic mesh is practically impossible. Therefore, by analogy with definition (2) is physically more correctly we only consider the maximum size of the cell edge:
![]() . (9)
. (9)
Here аmах is maximum element size.
The expression (9) for example tetrahedral mesh is a kind of generalization of the two definitions scale D. This eliminates the need to calculate the subgrid scale for each grid cell.
Example of constructing a structured mesh for the computational domain of landfill PTO-1 (St. Petersburg) is shown in Figure 2.

Figure 2 – Example of a structured grid (built in Comsol Multiphysics)
To construct the proposed structured grid should adhere to the following rules:
1. The growth rate of TBE tetraedricheskoy grid responsible for the degree of thickening, taken strictly equal to 1.
2. The maximum line size amah given considerably smaller than the calculated area to get a thick, close to the isotropic mesh.
To subgrid turbulent viscosity considered isotropic must comply with condition kхуz = const. This condition can be performed using the calculation of velocity field Lagrangian finite elements with linear approximation. In this case, within each end element derivatives of the velocity components и, v и w on the coordinate axes are constants then Dеf = const then kхуz = const.
Asking subgrid isotropic of turbulent viscosity and reduces the computation time for the approximation of the finite element method of the differential equation of turbulent diffusion, as eddy viscosity within a finite element can be considered constant.
References
- Гарбарук А.В. Моделирование турбулентности в расчётах сложных течений / А.В.Гарбарук, М.Х.Стрелец, М.Л.Шур. – СПб.: Изд-во Политехн. ун-та, 2012. – 88 c.
- Peyret, R. Computational Methods for Fluid Flow / R.Peyret, T.Taylor. –New York: Springer-Verlag, 1983. – 358 p.


