Целью работы является исследование позиционирования шлифовального круга при обработке винтовых стружечных канавках с постоянным углом наклона на эллипсоидных борфрезах.

Результаты исследования сделают процесс позиционирования более наглядным и послужат основой разработки программ ЧПУ для различных станков.

Задачами работы являются выведение необходимых математических операций позиционирования шлифовального круга, и проверка расчетов в среде 3D моделирования T-flex CAD.

Для проведения расчетов представим дно винтовой стружечной канавки эллипсоидной борфрезы в виде эллипсоида с вершиной в точке  начала общей системы координат , а шлифовальный круг в виде усеченного конуса со своей системой координат  с вершиной в точке центра его основания , совпадающей с точкой . В начальном положении  находиться в начале общей системы координат и направления осей сонаправлены общим  соответственно, как показано на рис. 1.

Для математического представления поворотов и перемещений использовался матричный метод представления. При позиционирования шлифовального круга необходимо выполнить следующие преобразования его системы координат  в каждой точке, относительно траектории винтовой стружечной канавки с постоянным углом наклона:

1.        Поворот на угол касательной к эллипсоиду  вокруг оси ;

2.        Поворот на угол наклона винтовой канавки  вокруг оси ;

3.        Поворот на угол  вокруг оси ;

4.        Перемещение в рассматриваемую точку на эллипсоиде;

5.        Перемещение по  на расстояние равное радиусу шлифовального круга;

6.        Перемещение в конечную точку от поворота на угол .

Первым шагом в позиционировании является поворот системы координат шлифовального круга  на угол касательной к эллипсоиду. В плоскости  уравнение эллипса, смещённого относительно начала координат вправо, выглядит следующим образом:

(1)

где  – большая полуось эллипса,  – малая полуось эллипса,  – координата рассматриваемой точки по оси , y – координата рассматриваемой точки по оси .

Выразив y, получаем выражение:

(2)

Отсюда находим угол наклона касательной :

(3)

Матрица вращения вокруг оси круга  выглядит следующим образом:

(4)

где  – угол поворота.

Представляем оси системы координат начального положения шлифовального круга  в виде единичных векторов ,  и . Умножаем матрицу  на каждый вектор по отдельности. Получаем вектора ,  и :

(5)

На рис.2 показана схема поворота системы координат шлифовального круга на угол касательной к эллипсу .

Рис. 2 Поворот на угол kas

Чтобы задать угол наклона винтовой канавки , нужно повернуть систему координат  на угол вокруг вектора  для этого напишем матрицу :

(6)

где ,  и  точки задающие положение единичного вектора , направленного по нормали к точке на эллипсе.

Поворачиваем систему координат  на угол наклона винтовой канавки , перемножив на матрицу :

(7)

Рис. 3 Поворот на угол наклона винтовой канавки w

Выполненных поворотов достаточно для образования канавки нужного профиля. Однако, тогда бы требовалось дополнительное, редко присутствующее, движение на станке для вращения круга в процессе обработке вокруг оси  так, чтобы вектор  был всегда направлен по нормали к эллипсу. Чтобы уйти от него поворачиваем систему координат круга на угол  вокруг оси  таким образом, чтобы вектор  лежал в плоскости . Вычисляем угол :

(8)

где  и проекции вектора  на оси  и  соответственно.

Матрица поворота на угол  вокруг оси Х выглядит так:

(9)

Поворачиваем систему координат  на угол , перемножив на матрицу :

(10)

Вектора  задают положение системы координат шлифовального круга после всех поворотов. На рис.4 представлен поворот круга на угол :

Рис. 4 Поворот системы координат круга  на угол 

Предыдущие преобразования мы делали в начале системы координат . Теперь нужно переместить систему координат шлифовального круга  в нужное положение относительно заготовки. Потребуется матрица перемещения в рассматриваемую точку на эллипсе:

(11)

 – координата рассматриваемой точки по оси , y – координата рассматриваемой точки по оси .

Перейдём к матрице перемещения на радиус шлифовального круга по нормали к эллипсу . В качестве нормали используем вектор . Чтобы задать значения перемещения нужно разложить вектор по значению равный радиусу шлифовального круга  направленный по нормали  на составляющие  и :

	(12)

Таким образом матрица  будет равна:

(13)

Последнее перемещение нужно после поворота на угол  вокруг оси , его можно рассчитать следующим образом:

	(14)

где  и  параметры на которые нужно переместить центр круга по оси  и  соответственно.

Тогда последняя матрица перемещения  будет равна:

(15)

Применим расчеты для начальной точки , получив :

(16)

Наглядно перемещения начальной  представлены на рис. 5.

а)	б)	в)
Рис. 5 Схема перемещения центра круга :а) – перемещение в точку касания на эллипсе с помощью матрицы ; б) – перемещение по нормали к эллипсу  на величину равную радиусу круга ; в) – перемещение после поворота на угол .

В целях проверки полученных матричных преобразований проведём аналогичные действия в среде 3-х мерного параметрического моделирования T-flex CAD и сверим результаты. Для этого зададим конкретные значения параметров (табл. 1):

Исходные данные			Таблица 1
Переменная	Значение	Описание
a	25	Большая полуось эллипса
b	10	Малая полуось эллипса
R	30	Радиус шлифовального круга
w	30	Угол наклона винтовой стружечной канавки

По ним рассчитаем направления осей системы координат , и положение точки центра круга . Результаты расчета представлены в табл. 2.

Результаты расчета			Таблица 2
Переменная	Значение	Описание
	(0.697; -0.649; 0.303)	Единичный вектора системы координат шлифовального круга 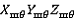 выходящие из точки (0; 0; 0).
	(0.595; 0.760; 0.259)
	(-0.399        ; 0; 0.917)
	(-14.862; 27.247; -9.683)	Центр основания шлифовального круга

Результат визуализации представлен на рис. 6.

Рис. 6 Визуальное представление в среде T-flex CAD

Модель обработки выглядит предполагаемым образом и все численные результаты совпадают с расчетными. Следовательно, расчетные данные верны и ими можно оперировать при написании программы ЧПУ.

1. Петухов, Ю.Е. Формообразование численными методами / Ю.Е. Петухов. – М. : «Янус-К», 2004. – 200 с.
2. Гречишников, В.А. Математическое моделирование в инструментальном производстве / В.А. Гречишников, Н.В. Колесов, Ю.Е. Петухов. – М. : МГТУ «СТАНКИН». УМО АМ, 2003. – 116 с.
3. Петухов, Ю.Е. Проектирование инструментов для обработки резанием деталей с фасонной винтовой поверхностью на стадии технологической подготовки производства : дис. … докт. техн. наук : 05.03.01 / Ю.Е. Петухов. – М., 2004. – 393 с.
4. Петухов, Ю.Е. Численные модели режущего инструмента для обработки сложных поверхностей / Ю.Е. Петухов, Н.В. Колесов // Вестник машиностроения. – 2003. – №5. – С. 61-63.
5. Петухов, Ю.Е. Профилирование режущих инструментов среде Т-flex CAD-3D / Ю.Е. Петухов // Вестник машиностроения. – 2003. – №8. – С. 67-70.
6. Петухов, Ю.Е. Способ формообразования фасонной винтовой поверхности стандартным инструментом прямого профиля / Ю.Е. Петухов, П.В. Домнин // Вестник МГТУ «СТАНКИН». – 2011. – №3. – С. 102-106.
7. Колесов, Н.В. Система контроля сложных кромок режущих инструментов / Н.В. Колесов, Ю.Е. Петухов // ИТО: Инструмент. Технология. Оборудование. – 2003. – №2. – С. 42-45.
8. Петухов, Ю.Е. Компьютерная модель формообразования сложной поверхности / Ю.Е. Петухов, П.В. Домнин // Международная научно-техническая конференция «Автоматизация: проблемы, идеи, решения». В 2 т. : сб. науч. ст. – Тула, 2010. – Т. 1. – С. 197-200.
9. Колесов, Н.В. Компьютерная модель дисковых фасонных затылованных фрез / Н.В. Колесов, Ю.Е. Петухов, А.В. Баринов // Вестник машиностроения. – 1999. – №6. – С. 57-61.
10. Домнин, П.В. Решение обратной задачи профилирования на базе схемы численного метода заданных сечений / П.В. Домнин, Ю.Е. Петухов // Справочник. Инженерный журнал с приложением. – 2011. – №11. – С. 26-29.
11. Колесов, Н.В. Математическая модель червячной фрезы с протуберанцем / Н.В. Колесов, Ю.Е. Петухов // СТИН. – 1995. – №6. – С. 26-29.
12. Колесов, Н.В. Два типа компьютерных моделей режущего инструмента / Н.В. Колесов, Ю.Е. Петухов // СТИН. – 2007. – №8. – С. 23-26.
13. Петухов, Ю.Е. Точность профилирования при обработке винтовой фасонной поверхности / Ю.Е. Петухов, П.В. Домнин // СТИН. – 2011 – №7. – С. 14-17.
14. Петухов, Ю.Е., Математическая модель криволинейной режущей кромки спирального сверла повышенной стойкости / Ю.Е. Петухов, А.А. Водовозов // Вестник МГТУ «СТАНКИН». – 2012. – №3. – С. 28-32.
15. Петухов, Ю.Е. Некоторые направления развития САПР режущего инструмента / Ю.Е. Петухов // СТИН. – 2003. – №8. – С. 26-30.
16. Петухов, Ю.Е. Затачивание по передней поверхности спиральных сверл с криволинейными режущими кромками / Ю.Е. Петухов, А.А. Водовозов // Вестник МГТУ «СТАНКИН». – 2014. – №1 (28). – С. 39-43.
17. Petukhov, Y.E. Shaping precision in machining a screw surface / Y.E. Petukhov, P.V. Domnin // Russian Engineering Research. – 2011. – T. 31. – №10. – С. 1013-1015.
18. Kolesov, N.V. Computer models of cutting tools / N.V. Kolesov, Y.E. Petukhov // Russian Engineering Research. – 2007. – T. 27. – №11. – С. 812-814.
19. Petukhov, Y.E. Determining the shape of the back surface of disc milling cutter for machining a contoured surface / Y.E. Petukhov, A.V. Movsesyan // Russian Engineering Research. – 2007. – T. 27. – №8. – С. 519-521.

Все статьи автора «Бега Алексей Павлович»