В последнее время в трансмиссиях транспортно-технологических машин начали широко использовать планетарные передачи, среди которых наиболее распространёнными являются передачи типа 2К-Н. Такие передачи, как правило, применяют в бортовых редукторах, устанавливаемых на выходе из трансмиссий.

Характерной особенностью функционирования планетарных передач является нагружение выходного вала значительной по величине радиальной силой (P), которая зависит от передаваемого крутящего момента (T), силы тяжести машины, приходящейся на ведущие колёса, их ударов в дорожные препятствия, для гусеничных машин – статического натяжения гусениц и, в связи с этим, носит переменный характер. Под действием радиальной силы происходят деформации деталей корпуса бортового редуктора, опор валов и в результате этого взаимные отклонения зубчатых колёс в торцовой, общей нормальной и общей касательной плоскостях, что сказывается на характере нагруженности  зубьев колёс и должно учитываться при проектировании.

Одним из важнейших критериев работоспособности зубчатых колёс бортовых редукторах является ресурс их работы. Выбор оптимальных параметров зубчатых колёс возможен при условии правильного определения эквивалентных чисел циклов перемены напряжений в зубьях с учетом переменного характера окружных усилий в зацеплениях, переменного характера распределения нагрузки по ширине венцов и переменного характера неравномерности нагружения сателлитов.

Установление влияния указанных факторов с учетом существующих между ними связей на величины контактных напряжений и напряжений изгиба зубьев обуславливает комплексный характер решаемой задачи. Для её решения необходима разработка математической модели, описывающей состояние объекта исследования с учетом внутренней структуры и взаимосвязей между структурными составляющими.

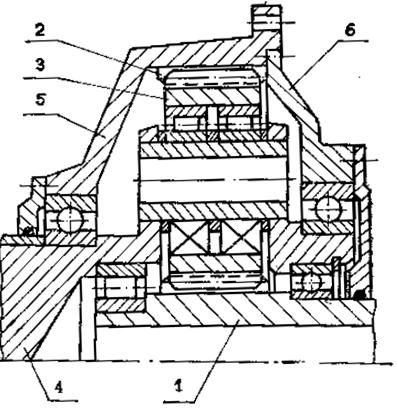
На основании анализа методов расчета зубчатых колес передач на выносливость [1, с. 3, 5], а также методов определения распределения нагрузки по ширине венцов и неравномерности нагружения сателлитов планетарных передач [2, с.88] принимается, что напряжения в зубьях зависят от следующих основных факторов: нагрузок, действующих на передачу (внешних); нагрузок, действующих на детали (внутренних); деформаций деталей; перекосов и смещений деталей; распределения нагрузок по ширине венцов и неравномерности нагружения сателлитов. Связи между факторами устанавливаются применительно к планетарной передаче типа 2К-Н бортового  редуктора, представленного на рисунке 1. В таком редукторе солнечная шестерня является быстроходным (ведущим) валом эпициклическая шестерня выполнена в картере, а на вал водила устанавливается ведущее колесо.

Конструкция планетарной передачи типа 2К – Н бортового редуктора транспортно-технологической машины: 1 – солнечная шестерня; 2 – эпициклическая шестерня; 3 – сателлит; 4 – водило; 5 – картер; 6 – крышка картера.

Рисунок 1.

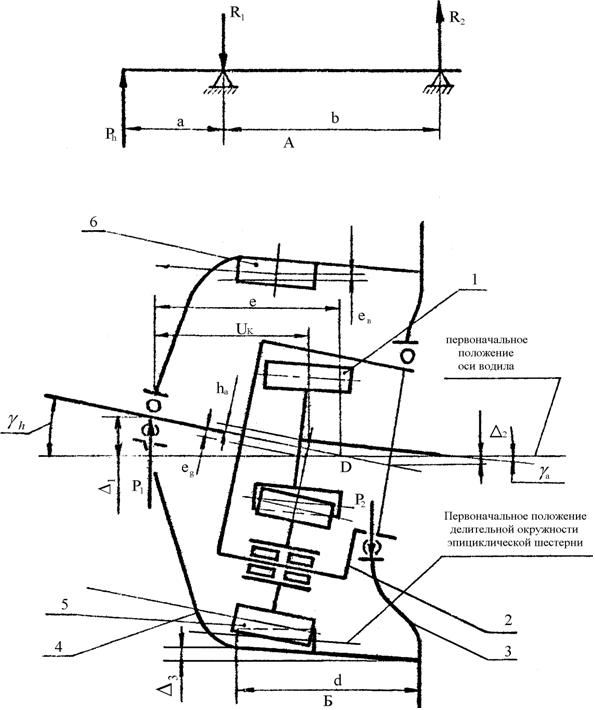
К числу внешних нагрузок, действующих на бортовой редуктор, относятся крутящий момент на ведущем валу Т и радиальная сила P, нагружающая водило, являющиеся случайными функциями времени t. Схема перекосов и смещений зубчатых колес планетарной передачи при нагружении водила радиальной силой представлена на рисунке 2. Для разработки методики, учитывающей названные факторы необходимо рассмотреть процесс формирования контактных напряжений в полюсах зацеплений и напряжений изгиба зубьев [3].

Внешние нагрузки Т и P_h приводят к возникновению в бортовом редукторе внутренних нагрузок – окружных и радиальных сил. Так, окружными силами нагружаются солнечная шестерня , сателлиты – , эпициклическая шестерня –  и водило –  (связи 1, 2, 3, 4). Окружные силы  приводят к деформациям скручивания солнечной шестерни  (связь 5). В результате неравных окружных сил   происходит перемещение зубчатого венца плавающей солнечной шестерни в торцовом сечении (связь 6), при этом она может перекашиваться относительно продольной оси передачи на некоторый угол γ_a. Под действием окружных сил  возникает деформация взаимного смешения щек водила ∆_д (связь 7).

Схема перекосов зубчатых колес планетарной передачи типа 2К-Н бортового редуктора при нагружении водила радиальной силой: А – нагрузки, действующие на водило; Б – перекосы колес; 1,5,6 – зубчатые венцы солнечной шестерни, сателлита и эпициклической шестерни соответственно; 2 – водило; 3 – крышка картера; 4 – картер.

Рисунок 2.

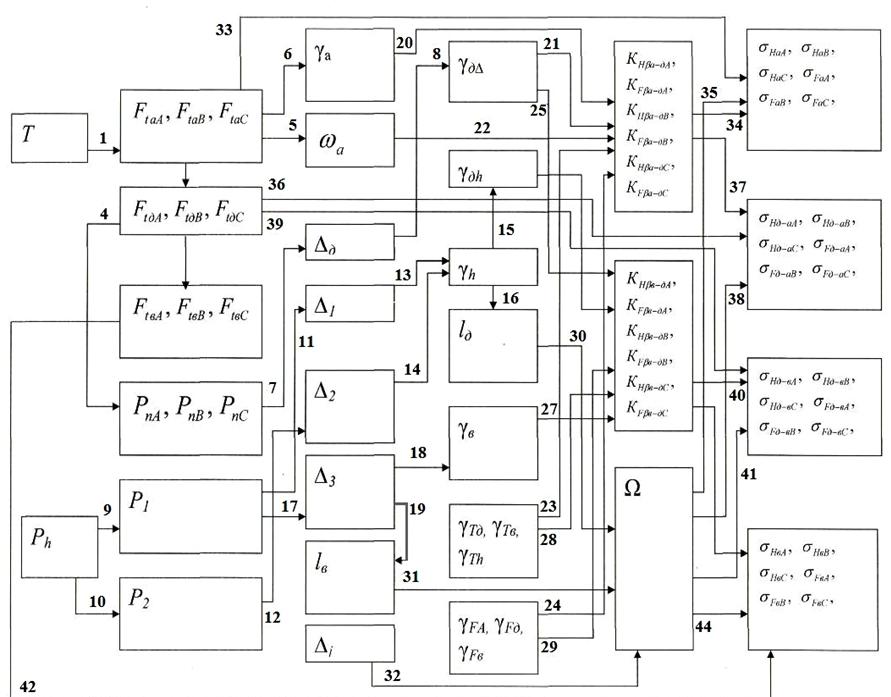
Разработанная блок-схема алгоритма расчета формирования контактных напряжений и напряжений изгиба зубьев в такой  передаче представлена на рисунке 3.

Схема формирования контактных напряжений и напряжений изгиба зубьев планетарной передаче типа 2К-Н бортового редуктора

Рисунок 3. Блок-схема расчета  контактных напряжений

В результате действия радиальной силы P_h нагружается картер и крышка картера радиальными силами, соответственно Р₁, и Р₂ (связи 9, 10). Эти силы вызывают перемещения опор водила в картере ∆₁, и крышке картера ∆₂ (связи 11, 12). Причиной таких перемещений являются деформации деталей (картера, крышки картера и установленных в них подшипников), радиальные зазоры в подшипниках, а также между их обоймами и сопрягаемыми деталями. При этом водило перекашивается на угол γ_h (связи 13, 14), вместе с ним на угол γ_дh  перекашиваются сателлиты (связь 15). Радиальная жесткость картера и крышки картера, как правило, не равны между собой, также не равны расстояния между серединной плоскостью сателлитов и опорами водила. Поэтому при перекосах водила на угол γ_h происходит смещение сателлитов в торцовом сечении на величину  l_д (связь 16). Под действием радиальной силы, нагружающей картер P_h, происходит его радиальная деформация ∆₃(связь 17), которая приводит к перекосу эпициклической шестерни на угол  γ_в (связь 16), а также смещению эпициклической шестерни в торцовом сечении на величину l_в (связь 19).

На распределение нагрузки по ширине венцов в зацеплении солнечной шестерни с сателлитами   влияют: угол перекоса солнечной шестерни γ_а, деформация скручивания солнечной шестерни ω_а, угол перекоса сателлитов γ_д∆    от деформации взаимного смещения щек водила, углы перекосов сателлитов γ_Т∆, эпициклический шестерни γ_Тв и водила γ_Тh   в результате отклонений размеров деталей от номинальных значений, а также отклонения зубьев солнечной шестерни γ_Fa, сателлитов γ_Fд   и эпициклической шестерни γ_Fв   от заданного направления (связи 20, 21,22, 23, 24). На распределение нагрузки по ширине венцов в зацеплении эпициклической шестерни с сателлитами  влияют: угол перекоса сателлитов γ_д∆ от деформации взаимного смещения щек водила, угол перекоса сателлитов с водилом γ_дh угол перекоса эпициклической шестерни γ_в от радиальной деформации картера, углы перекосов сателлитов γ_Тд эпициклической шестерни γ_Тв и водила γ_Тh в результате отклонений размеров деталей от номинальных значений, а также отклонения зубьев солнечной шестерни γ_Fa, сателлитов  γ_Fд  и эпициклической шестерни γ_Fв от заданного на­правления (связи 25, 26, 27, 28, 29). На неравномерность нагружения сателлитов Ω влияют: их смещение l_д торцовом сечении с водилом, смещение эпициклической шестерни в торцовом сечении l_в от деформации картера в радиальном направлении, а также начальные боковые зазоры ∆_i в зацеплениях солнечной и эпициклической шестерен с сателлитами (связи 30, 31, 32).

На величины контактных напряжений в полюсе зацепления и величины напряжений изгиба зубьев колес планетарной передачи влияют окружные силы, распределение нагрузки по ширине венцов и неравномерность нагружения сателлитов. Поэтому напряжения σ_H и σ_F рассматриваются зависящими от следующих параметров:

- для зубьев солнечной шестерни

(связи 33, 34, 35);

-  для зубьев сателлитов в зацеплении с солнечной шестерней

(связи 36, 37, 38);

- для зубьев сателлитов в зацеплении с эпициклической шестерней

(связи 39, 40, 41);

- для зубьев эпициклической шестерни

(связи.42, 43, 44).

Для расчета зубьев колес планетарных передач бортовых редукторов с учетом влияния, оказываемого крутящим моментом и радиальной силой, нагружающей водило, на величины напряжений в зубьях требуется математическое описание каждой из установленных связей. В том числе необходимо уточнение связей 9-19, 26, 27, 30, 31, 35, З8, 40, 41, 43, 44 с учетом влияния, оказываемого радиальной силой. Для этого необходимо дальнейшее проведение теоретических и экспериментальных исследований.

Одной из тенденций совершенствования конструкций современных колёсных и гусеничных транспортно-технологических машин является повышение их быстроходности и проходимости при обеспечении заданной грузоподъёмности и собственной массы. Обеспечение таких эксплуатационных свойств связано с решением при конструировании противоречивых задач и достигается поиском принципиально новых конструкторских решений в части выбора более рациональных кинематических схем, оптимизации конструкций деталей, а также применением материалов с более совершенными свойствами [4, 5].

Все статьи автора «gorgotz»