В задах сейсмики сооружений [1,2,3,4,5], ветровых колебаний [6,7], или в физически нелинейных задачах при учете истории нагружения [8, 9,10] необходимо отслеживать состояние системы с оценкой устойчивости.
Строительные конструкции из железобетона или из стали, работающей в упруго-пластической стадии, являются нелинейными и неконсервативными механическими системами. Нагрузки на эти конструкции часто не описываются однопараметрическим способом. Поэтому бифуркационная модель исследования устойчивости не всегда может с достаточной точностью оценивать характер равновесия таких механических систем. Наиболее точно произвести оценку состояния и устойчивости здесь позволяет динамический подход, в том случае если с удовлетворительной полнотой воспроизвести инерционные и демпфирующие свойства системы.
Для оценки устойчивости указанных сооружений целесообразно исследовать их отклики на приращение векторов кинематических параметров данного равновесного состояния элементов. Предпочтение кинематического возмущения перед силовым обусловливается двумя основными причинами: во-первых, природа потери устойчивости второго рода связана с развитием ранее достигнутых деформаций; во-вторых, перебрать все возможные направления силовых возмущений практически нельзя из-за их многообразия. Для ответа на вопрос: «Устойчива ли данная система по отношению к кинематическому возмущению?» – необходимо выполнить следующие операции:1) дать кинематическое возмущение (приращения к перемещениям) данному равновесному состоянию;
2) исследовать движение системы в течение определённого промежутка времени. Этот промежуток времени является периодом предельно низкой допустимой частоты колебаний данной механической системы;Если система, в течение указанного времени, совершила колебательное движение – она устойчива. В противном случае система неустойчива.
Другими словами здесь оценивается наличие и достаточность обобщённой восстанавливающей силы (для непередемпфированных систем).
Данное исследование удобно строится на основе метода сеточной аппроксимации элементов в динамической постановке.
Пусть заданное исходное состояние элемента конструкции описывается векторной функцией:
![]() , (1)
, (1)
где .gif)
.gif) (2)
(2)
n – мерные вектора продольного и двух поперечных перемещений точек продольной оси и угла поворота сечения стержня вокруг этой оси.
Если не выделять приоритетно какие-либо перемещения, то возмущённая векторная функция (1) может быть записана в виде:
где k – коэффициент (модуль) возмущения, k>1.
При назначении коэффициента возмущения нет определённых критериев, однако, при исследовании устойчивости данного положения равновесия целесообразно брать его достаточно близким к единице.
При использовании гипотезы плоских сечений продольные деформации в точках сечения элемента в данном равновесном состоянии определяются зависимостью:
![]() , (4)
, (4)
представленной в конечно-разностном виде, а деформации возмущённого состояния равенством
![]() . (5)
. (5)
В динамическом расчёте кинематически возмущённое состояние является начальным условием движения.
Уравнения движения элемента системы из возмущённого состояния имеют вид:
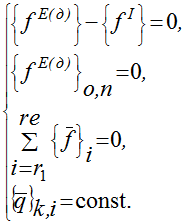 (6)
(6)Для решения задачи используются или двойная конечно-разностная аппроксимация функций перемещений и их производных по геометрической и временной координатам, или метод линейного ускорения. Таким способом делается переход от интегро-дифференциальных уравнений к интегральным. При помощи дополнительных сеток, наложенных на поперечные сечения и боковые грани участка стержня, задача сводится к решению алгебраической системы уравнений.
В начальный момент времени
Производя движение по временной координате от ![]() до
до ![]() , определяем характер движения. Характер движения из возмущённого положения даёт возможность классифицировать исходное состояние равновесия с точки зрения его устойчивости.
, определяем характер движения. Характер движения из возмущённого положения даёт возможность классифицировать исходное состояние равновесия с точки зрения его устойчивости.
Библиографический список
- Шеин А.И. Метод сеточной аппроксимации элементов в задачах строительной механики нелинейных стержневых систем // М-во образования и науки Рос. Федерации, Федер. агентство по образованию, Пенз. гос. ун-т арх. и стр-ва. – Пенза, – 2005. – 248 стр.
- Шеин, А.И. Решение многопараметрической задачи динамики стержневых систем методом сеточной аппроксимации элементов //Промышленное и гражданское строительство. – 2002. – № 2. – С.- 27.
- Шеин, А.И. Оценка эффективности активного жидкостного гасителя колебаний высотных сооружений при нестационарных воздействиях/ А.И. Шеин, Д.А. Шмелев // Строительная механика и расчет сооружений. – 2014. - №1(252). – С. 59-63.
- Шеин, А.И. Гашение колебаний высотных сооружений в 3 ч. / А. И. Шеин [и др.] // М-во образования и науки Российской Федерации, Гос. образовательное учреждение высш. проф. образования “Пензенский гос. ун-т архитектуры и стр-ва”.- Пенза, – 2011
- Шеин, А.И. Метод смещенных разностей для решения систем дифференциальных уравнений движения механических систем / А.И. Шеин, М.Б. Зайцев // Строительная механика и расчет сооружений. – 2012.- №2. – С. 38-41.
- Шеин, А.И. Схемы и теория гасителей пространственных колебаний сооружений / А.И. Шеин, О.Г. Земцова// Региональная архитектура и строительство. -2010. - №1. – С. 45-52.
- Шеин, А.И. Снижение уровня колебаний системы “упругое основание – высотное сооружение” с помощью нелинейного динамического гасителя / А.И. Шеин, О.Г. Земцова //. Региональная архитектура и строительство.- 2011.- № 2.- С. 83-90.
- Завьялова, О.Б. Применение условного сдвиго-изгибного стержня при расчете рам на устойчивость / О.Б. Завьялова, А.И. Шеин .//Известия высших учебных заведений. Строительство. -2010.- №1. С. 99-105.
- Шеин, А.И. Влияние физической нелинейности бетона на напряженно-деформированное состояние элементов монолитных железобетонных рам, рассчитываемых с учетом истории нагружения / А. И. Шеин, О.Б. Завьялова// Промышленное и гражданское строительство. – 2012.- №8.- С. 29-31.
- Шеин, А.И. Расчет монолитных железобетонных каркасов с учетом последовательности возведения, физической нелинейности и ползучести бетона/ А. И. Шеин, О.Б. Завьялова // Строительная механика и расчет сооружений. 2012. № 5. С. 64-69.


