Целью работы является: проверить корректность математических исчислений нарезания винтовых стружечных канавок с постоянным углом наклона на эллипсоидных борфрезах, отобразив их результат в среде параметрического 3D моделирования T-Flex CAD. Проверка такого рода позволяет апробировать математику перед этапом практического изготовления инструмента на станке.
Задачами работы является: приведение математики к виду адаптированному для 5-ти координатного станка LTF SPA U320/V и среды T-Flex CAD; моделирование эллипсоидной борфрезы с винтовыми стружечными канавками постоянного угла наклона в среде T-Flex CAD по данной математике; измерение геометрии зубьев полученной модели и соотнесение их с общепринятыми.
Для описания движений в процессе обработки были выведены формулы описывающие движение шлифовального круга вокруг неподвижной заготовки.
Выбранный станок обладает следующими движениями: продольное движение вдоль оси заготовки, круговое движение вокруг оси заготовки, вертикальное движение абразивного круга, горизонтальное движение абразивного круга, вращение стола заготовки.
Для проведения расчетов представим стружечную канавку в виде винтовой линии на эллипсоиде с переменным шагом P и постоянным углом наклона w.
Для расчёта угла поворота заготовки ![]() , возьмём интеграл от скорости вращения при постоянной подачи, по которому впоследствии получим угол поворота заготовки вокруг своей оси для станка (1).
, возьмём интеграл от скорости вращения при постоянной подачи, по которому впоследствии получим угол поворота заготовки вокруг своей оси для станка (1).
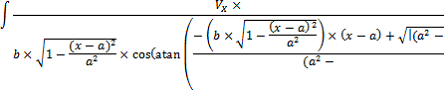 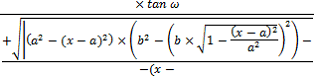 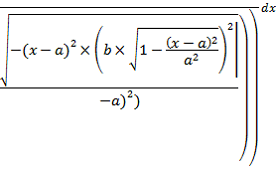 |
(1) |
где ![]() – скорость подачи,
– скорость подачи, ![]() – большая полуось эллипсоида сердцевины,
– большая полуось эллипсоида сердцевины, ![]() – малая полуось эллипсоида сердцевины,
– малая полуось эллипсоида сердцевины, ![]() – угол наклона винтовой канавки,
– угол наклона винтовой канавки, ![]() – координата положения рассматриваемой точки на продольной оси заготовки.
– координата положения рассматриваемой точки на продольной оси заготовки.
Дно винтовой стружечной канавки эллипсоидной борфрезы имеет вид эллипсоида с вершиной в точке ![]() начала общей системы координат
начала общей системы координат ![]() , а шлифовальный круг в виде усеченного конуса со своей системой координат
, а шлифовальный круг в виде усеченного конуса со своей системой координат ![]() с вершиной в точке центра его основания
с вершиной в точке центра его основания ![]() , совпадающей с точкой
, совпадающей с точкой ![]() . В начальном положении
. В начальном положении ![]() находиться в начале общей системы координат и направления осей сонаправлены общим
находиться в начале общей системы координат и направления осей сонаправлены общим ![]() соответственно, как показано на рис. 1.
соответственно, как показано на рис. 1.
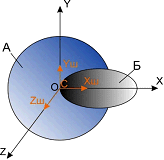
Рисунок 1 – Начальное положение: А – шлифовального круга; B – борфрезы
Для математического представления поворотов и перемещений использовался матричный метод представления. При позиционирования шлифовального круга были выполнены следующие преобразования его системы координат ![]() в каждой точке, относительно траектории винтовой стружечной канавки с постоянным углом наклона:1. Поворот на угол касательной к эллипсоиду
в каждой точке, относительно траектории винтовой стружечной канавки с постоянным углом наклона:1. Поворот на угол касательной к эллипсоиду ![]() вокруг оси
вокруг оси ![]() ;
;
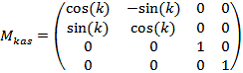 |
((2)
|
где ![]() – угол наклона касательной в точке на эллипсоиде.2. Поворот на угол наклона винтовой канавки
– угол наклона касательной в точке на эллипсоиде.2. Поворот на угол наклона винтовой канавки ![]() вокруг оси
вокруг оси ![]() ;
;
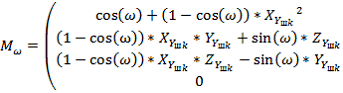 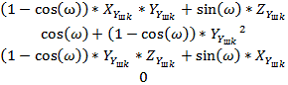 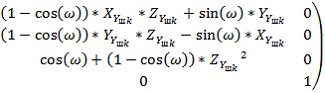 |
(3) |
где ![]() ,
, ![]() и
и ![]() точки задающие положение единичного вектора
точки задающие положение единичного вектора ![]() , направленного по нормали к точке на эллипсе.3. Перемещение в рассматриваемую точку на эллипсоиде;
, направленного по нормали к точке на эллипсе.3. Перемещение в рассматриваемую точку на эллипсоиде;
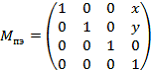 |
((4)
|
![]() – координата рассматриваемой точки по оси
– координата рассматриваемой точки по оси ![]() , y – координата рассматриваемой точки по оси
, y – координата рассматриваемой точки по оси ![]() .4. Перемещение по
.4. Перемещение по ![]() на расстояние равное радиусу шлифовального круга;
на расстояние равное радиусу шлифовального круга;
.gif) |
((5)
|
где ![]() и
и ![]() составляющие значения радиуса шлифовального круга
составляющие значения радиуса шлифовального круга ![]() направленного по нормали
направленного по нормали ![]() 5. Поворот на угол
5. Поворот на угол ![]() вокруг оси
вокруг оси ![]() :
:
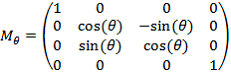 |
(6)
|
где ![]() .
.
Для моделирования процесса обработки в среде параметрического моделирования T-Flex CAD переведём все матричные исчисления в соответствующие формулы движения шлифовального круга по осям:
Перемещение по оси ![]()
Перемещение по оси ![]()
Перемещение по оси ![]()
Вращение вокруг оси ![]()
где угол ![]() задается массивом значений из определенного интеграла (1).
задается массивом значений из определенного интеграла (1).
Вращение вокруг оси ![]()
где ![]()
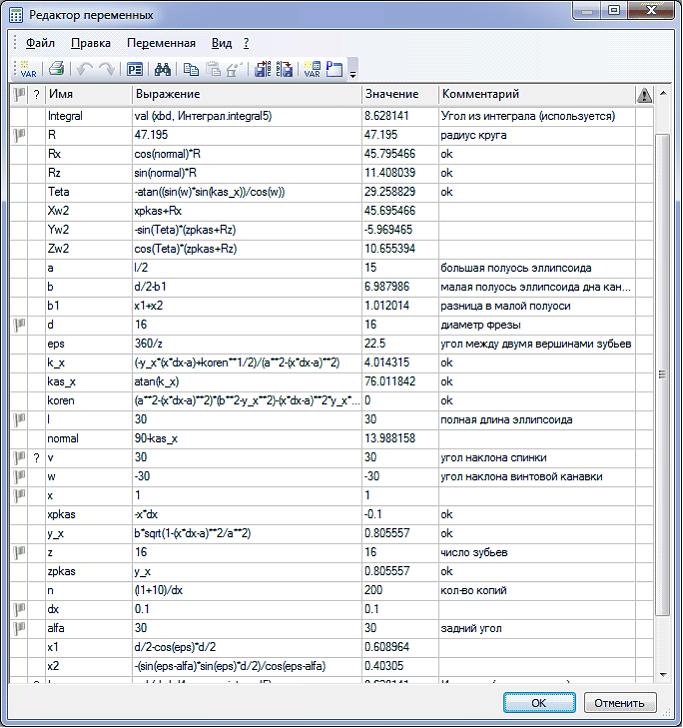
Создадим параметрическую модель, задав формулы движения через параметры (рис. 2) с исходными данными из табл. 1.
 |
|
Рисунок 2 – Задание переменных
|
|
Таблица 1 – Исходные данные
|
||
| Переменная | Значение | Описание |
| a | 30 мм | Большая полуось эллипса |
| b | 7 мм | Малая полуось эллипса |
| R | 47,195 мм | Радиус шлифовального круга |
| w | 30˚ | Угол наклона винтовой стружечной канавки |
| Z | 16 | Число зубьев |
| u | 60˚ | Угол профиля шлифовального круга |
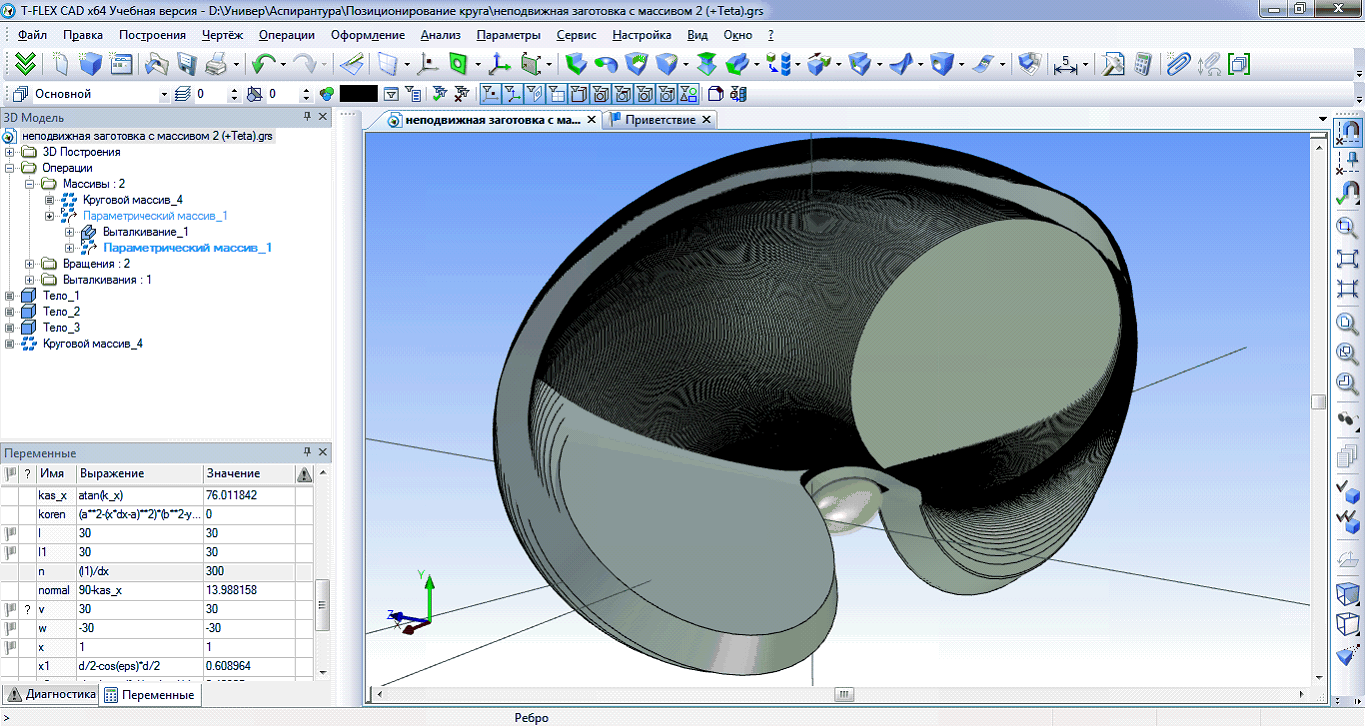
Имитацией процесса обработки служит булева операция вычитания из тела заготовки параметрического массива шлифовальных кругов при движении вокруг неподвижной заготовки рис. 3.
 |
|
Рисунок 3 – Массив шлифовальных кругов при формообразующем движении
|
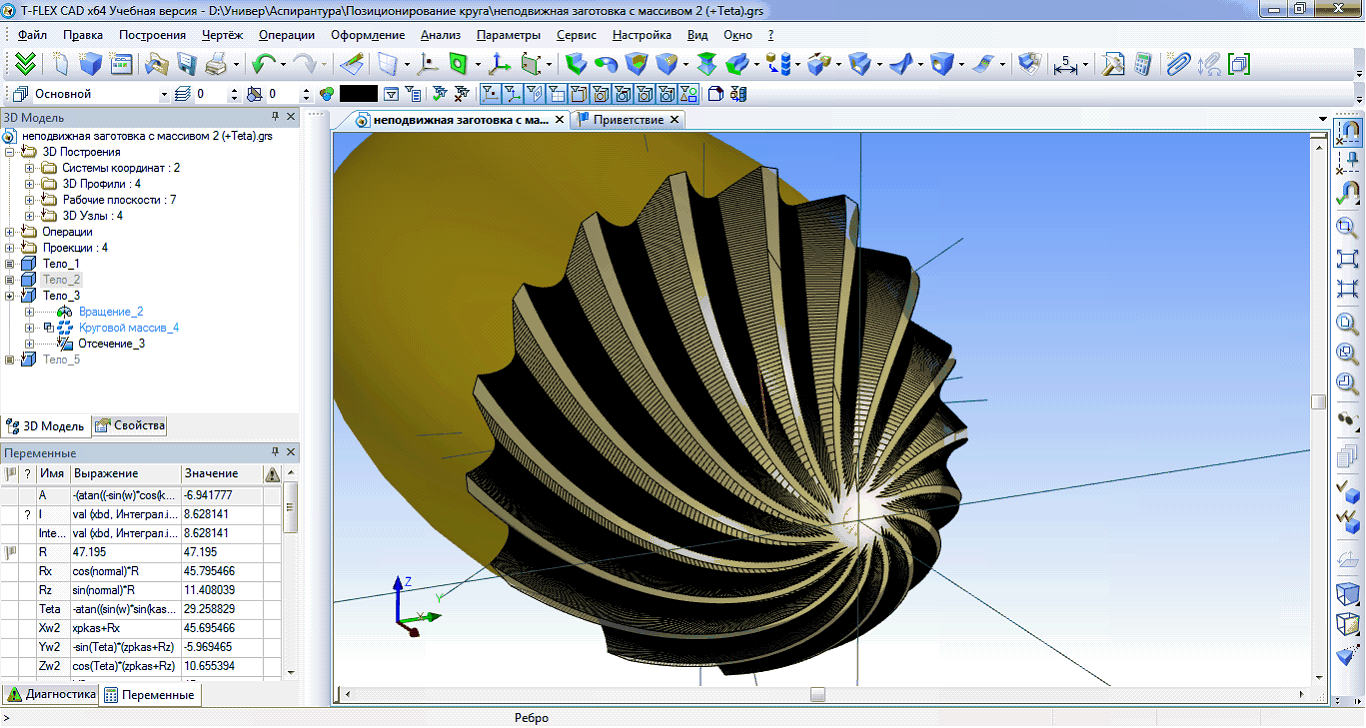
В результате булевой операции мы получили модель режущей части эллипсоидной борфрезы с постоянным углом наклона винтовых стружечных канавок рис. 4.
 |
|
Рисунок 4 – Модель режущей части фрезы
|
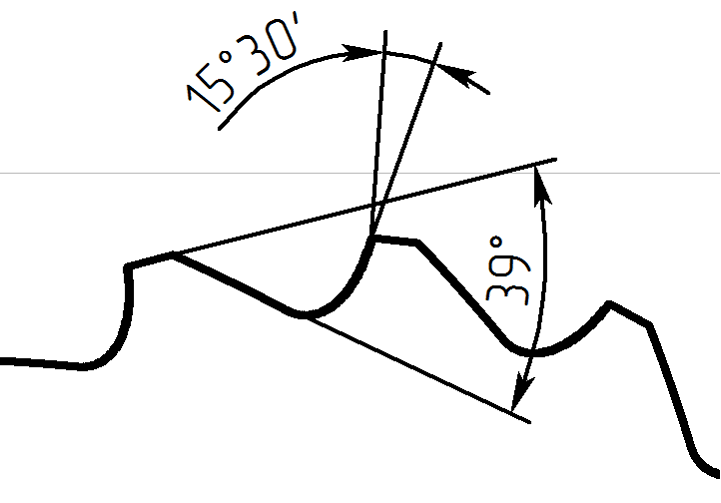
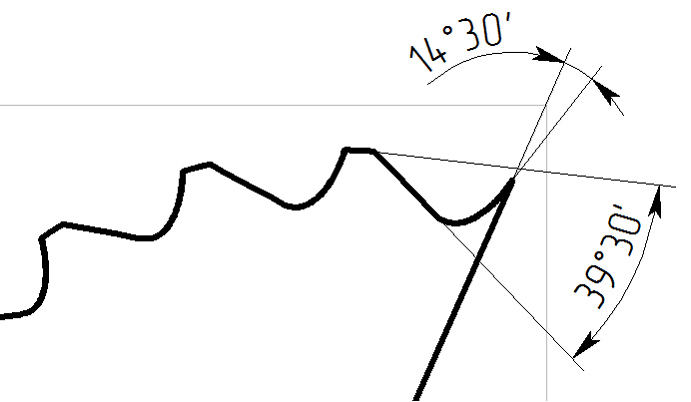
Рассмотрим геометрию полученных профилей зубьев модели в нормальном и радиальном сечениях и измерим значения передних и задних углов рис. 5.
 |
 |
|
а)
|
б)
|
|
Рисунок 5 – Геометрия зубьев: а) – в радиальном сечении; б) – в нормальном сечении
|
|
Как видно, из сравнения рис. 4а и 4б профиль модели соответствует установленным требованиям, при этом полученные значения углов совпадает с теоретическим. На основании приведенных данных можно сделать вывод о адекватности разработанной математической модели.
Библиографический список
- Петухов Ю.Е. Формообразование численными методами / Ю.Е. Петухов. – М. : «Янус-К», 2004. – 200 с.
- Петухов Ю. Е., Домнин П. В. Формообразование фасонных винтовых поверхностей инструментов на основе применения стандартных концевых и торцевых фрез. – М.: ФГБОУ ВПО МГТУ «СТАНКИН», 2012. -130с.
- Гречишников, В.А. Математическое моделирование в инструментальном производстве/ Гречишников В.А., Колесов Н.В., Петухов Ю.Е. – М.: МГТУ «СТАНКИН». УМО АМ, 2003. – 116 с.
- Петухов Ю.Е. Проектирование инструментов для обработки резанием деталей с фасонной винтовой поверхностью на стадии технологической подготовки производства :дис. … докт. техн. наук : 05.03.01 / Петухов Ю.Е.. – М., 2004. – 393с.
- Петухов Ю.Е. Численные модели режущего инструмента для обработки сложных поверхностей / Петухов Ю.Е., Колесов Н.В. // Вестник машиностроения. – 2003. – №5. – С. 61-63.
- Петухов Ю.Е. Профилирование режущих инструментов среде Т-flexCAD-3D / Петухов Ю.Е. // Вестник машиностроения. – 2003. – №8. – С. 67-70.
- Петухов, Ю.Е. Способ формообразования фасонной винтовой поверхности стандартным инструментом прямого профиля / Петухов Ю.Е., Домнин П.В. // Вестник МГТУ «СТАНКИН». – 2011. – №3. – С. 102-106.
- Колесов Н.В. Система контроля сложных кромок режущих инструментов / Колесов Н.В., Петухов Ю.Е. // ИТО: Инструмент. Технология. Оборудование. – 2003. – №2. – С. 42-45.
- Петухов Ю.Е. Компьютерная модель формообразования сложной поверхности / Петухов Ю.Е., Домнин П.В. // Международная научно-техническая конференция «Автоматизация: проблемы, идеи, решения». В 2 т. : сб. науч. ст. – Тула, 2010. – Т. 1. – С. 197-200.
- Колесов Н.В. Компьютерная модель дисковых фасонных затылованных фрез / Колесов Н.В., Петухов Ю.Е., Баринов А.В. // Вестник машиностроения. – 1999. – №6. – С. 57-61.
- Домнин П.В. Решение обратной задачи профилирования на базе схемы численного метода заданных сечений /Петухов Ю.Е., Домнин П.В. // Справочник. Инженерный журнал с приложением. – 2011. – №11. – С. 26-29.
- Колесов Н.В. Математическая модель червячной фрезы с протуберанцем / Колесов Н.В., Петухов Ю.Е. // СТИН. – 1995. – №6. – С. 26-29.
- Колесов Н.В. Два типа компьютерных моделей режущего инструмента Колесов/ Н.В., Петухов Ю.Е. // СТИН. – 2007. – №8. – С. 23-26.
- Петухов Ю.Е. Точность профилирования при обработке винтовой фасонной поверхности / Ю.Е. Петухов, П.В. Домнин // СТИН. – 2011 – №7. – С. 14-17.
- Петухов Ю.Е., Математическая модель криволинейной режущей кромки спирального сверла повышенной стойкости / Ю.Е. Петухов, А.А. Водовозов // Вестник МГТУ «СТАНКИН». – 2012. – №3. – С. 28-32.
- Петухов Ю.Е. Некоторые направления развития САПР режущего инструмента / Ю.Е. Петухов // СТИН. – 2003. – №8. – С. 26-30.
- Петухов Ю.Е. Затачивание по передней поверхности спиральных сверл с криволинейными режущими кромками / Ю.Е. Петухов, А.А. Водовозов // Вестник МГТУ «СТАНКИН». – 2014. – №1 (28). – С. 39-43.
- Петухов Ю.Е. Определение задних кинематических углов при обработке винтовых фасонных поверхностей стандартными фрезами прямого профиля./ Петухов Ю.Е., Домнин П.В.// Вестник МГТУ Станкин. 2014. № 2 (29). С. 27-33
- Петухов Ю.Е. Задачи по формообразованию при обработке резанием /Петухов Ю.Е., Колесов Н.В., Юрасов С.Ю.// Вестник машиностроения. 2014. № 3. С. 65-71.
- Петухов Ю.Е. Компьютерное моделирование обработки винтовой канавки на заготовке концевой фрезы./ Петухов Ю.Е, Домнин П.В.// Известия Московского государственного технического университета МАМИ. 2011. № 2. С. 156-164.
- Петухов Ю.Е. Cпособ шлифования фасонных валов. Патент на изобретение RUS863310 04.05.1979
- Петухов Ю.Е. Устройство для правки фасонных шлифовальных кругов. Патент на изобретение RUS 823101 21.03.1979
- Петухов Ю.Е. Способ обработки цилиндрических поверхностей патент на изобретение RUS 904999 04.05.1979
- Петухов Ю.Е. Прибор для профилирования червячных фрез. Патентнаизобретение RUS 878467 07.12.1978
- Petukhov Yu.E. Some directions of cutting tool cad system development./Petukhov Yu.E.// Russian Engineering Research. 2003. Т. 23. № 8. С. 72-76.
- Petukhov Yu.E. Curvilinear cutting edge of a helical bit with uniform life./Petukhov Yu.E.// Russian Engineering Research. 2014. Т. 34. № 10. С. 645-648.
- Kolesov N.V. The mathematical model of a hob with protuberances./Kolesov N.V., PetukhovYu.E.// Russian Engineering Research. 1995. Т. 15. № 4. С. 71-75
- Petukhov Y.E. Shaping precision in machining a screw surface / Y.E. Petukhov, P.V. Domnin // Russian Engineering Research. – 2011. – T. 31. – №10. – С. 1013-1015.
- Kolesov N.V. Computer models of cutting tools / N.V. Kolesov, Y.E. Petukhov // Russian Engineering Research. – 2007. – T. 27. – №11. – С. 812-814.
- Petukhov Y.E. Determining the shape of the back surface of disc milling cutter for machining a contoured surface / Y.E. Petukhov, A.V. Movsesyan // Russian Engineering Research. – 2007. – T. 27. – №8. – С. 519-521.


