Вступление
На сегодняшний день существует множество систем контроля процесса механообработки (ПМО), которые основаны на различных принципах роботы. Так контроль можно осуществлять, как по прямым выходным параметрам, так и по косвенным. Все они имеют свои преимущества и недостатки. Основным требованием к таким методам является адекватность их изменения при изменении состояния роботы объекта.
Данным требованиям, больше всего удовлетворяет метод анализа виброакустической эмиссии из зоны резания, так как виброакусический сигнал имеет незамедлительную реакцию на изменение состояния ПМО и инструмента. Недостатком данного метода является то, что для получения высокой точности и минимально искаженного сигнала, нужно измерительные устройства устанавливать непосредственно вблизи зоны резания. Это возможно осуществить лишь в лабораторных условиях, на производстве такое расположение регистрирующего датчика невозможно в связи с постоянной сменой инструмента и воздействиям на систему измерения, а конкретно на датчик, ТОС и внешних факторов.
Поэтому, датчик необходимо установить на место, которое защищено от воздействия неблагоприятных факторов. Это ведет к искажению и затуханию полезного виброакустического сигнала и ставит задачу по разработке математической модели прохождения сигнала от зоны резания до места измерения (по так называемой механической части акустического тракта измерительной системы).
Акустический тракт
Акустический тракт (АТ) представляет собой механическую часть измерительного канала от источника возникновения волнового движения до снимающего сигнал датчика. Природа прохождения сигнала по АТ является сложным явлением, так как обусловлена наличием множества условий, критериев и физических законов распространения акустической волны.
Проблема расчета АТ заключается в необходимости учета множества факторов для каждого конкретного случая. Анализ распространения волн в твердых системах осложняется тем, что они являются анизотропными. Поэтому параметры акустической волны проходиться выражать через тензорные величины.
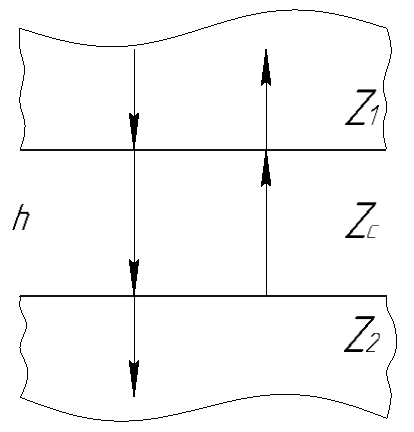
Акустический тракт может иметь n-е количество звеньев и переходов между ними (рис.1). Каждое звено характеризуется своим видом материала, что непосредственно влияет на его характеристики. Переход между средами образует собой границу раздела двух сред, разделенных тонким слоем. Большое влияние на прохождение виброакустического сигнала оказывает шероховатость и наличие загрязнений стыкуемых поверхностей в виде металлической стружки, масленой пленки и охлаждающей эмульсии.
Рис.1. Обозначения акустического тракта
При прохождении звуковой волны происходит ее затухание, связанное с различными необратимыми процессами. Часть энергии, которая переносится звуковыми волнами, поглощается средой. Величина, равная отношению поглощённой звуковой энергии к звуковой энергии, поступающей в среду, называется коэффициентом поглощения. Коэффициент поглощения зависит от внутренней вязкости среды и от её звукопроницаемости. Он так же зависит от скорости распространения звука в этой среде, от энергии и частоты звуковой волны.
Рассматривая спектр частот, следует упомянуть, что для инфразвука (ниже 16-20 Гц), характерно малое поглощение в различных средах, в связи, с чем он может распространяться на большие расстояния. В свою очередь, распространение ультразвуковых волн (от 16-20 кГц до 1 ГГц), в связи с малой длиной волны, существенно зависит от молекулярной структуры среды. Упругие волны, что лежат в диапазоне от 20 Гц до 16-20 кГц, по своей природе не отличаются от ультразвуковых волн, но имеют большую длину волны, что способствует распространенью, невзирая на структуру среды. Для построения нашей системы контроля ПМО с помощью виброакустического метода, более информативным является сигнал, что лежит в диапазоне частот инфразвука – вибрации элементов станка и упругих волн, воспринимаемых ухом человека – вибрации, что создаются при непосредственном проведении ПМО [1].
Акустические потери. Основной причиной поглощения акустических волн в твердых телах, являются силы вязкого сопротивления вибрации между соседними частицами, обладающими различными скоростями. Они выражаются через сопротивление внутреннего трения, действующее на частицы среды, в которой распространяется акустическая волна. Описание этого напряжение имеет вид:
где, за законом Гука cS – деформация (где c упругая постоянная материала), а η представляет собой коэффициент вязкости. Величины T и c являются тензорными, но могут быть представлены одной компонентой для одномерной продольной или поперечной волны.
Обусловленное потерями поглощение можно приближенно определить с использованием теоремы Пойтинга [2]. Коэффициент поглощения волны определяется выражением
![]()
где ω– круговая частота волны, Va – скорость распространения звуковой волны в данном теле, а ρ0 -плотность в стационарном состоянии объекта.
Таким образом, поглощение волны из-за потерь на внутреннее трение меняется пропорционально квадрату частоты и обратно пропорционально кубу скорости. Поскольку сдвиговые волны обычно имеют скорость порядка половины скорости распространения продольных волн в том же материале, можно ожидать, что поглощение сдвиговых волн на единицу длины будет значительно больше, чем продольных.
В реальных материалах имеется много других факторов, увеличивающих потери. Один из них — теплопроводность. Поглощение, обусловленное теплопроводностью, также изменяется пропорционально квадрату частоты. Еще одной причиной затухания является различие в теплопроводности и тепловом расширении соседних зерен, обусловленное поворотом их осей относительно друг друга. Поэтому высококачественные монокристаллические материалы характеризуются значительно меньшим затуханием звука, чем те же материалы в поликристаллической форме.
Акустический импеданс
Рассмотрим акустический импеданс Z для материала, который точнее следует называть удельным акустическим импедансом. Определим импеданс как представляющее собой отношение акустического давления pa к колебательной скорости частиц среды v при прохождении через нее звуковой волны:
В свою очередь акустическое давление pa определяется как произведение невозмущенной плотности среды и скорости распространения акустической волны в среде:
где ![]() - скорость смещения частиц среды;
- скорость смещения частиц среды;
![]() - постоянная распространения (волновое число) звука;
- постоянная распространения (волновое число) звука;
![]() - скорость распространения продольной волны (
- скорость распространения продольной волны ( ![]() -модуль объемной упругости либо, так называемый, модуль всестороннего сжатия).
-модуль объемной упругости либо, так называемый, модуль всестороннего сжатия).
Полученное соотношение (3) для плоской продольной волны остается верным и для плоских сдвиговых волн, если в нем скорость распространения продольной волны заменить на скорость распространения сдвиговой волны.
В расходящихся сферических и цилиндрических волнах акустическое давление и колебательная скорость частиц среды изменяются несинфазно и акустическое сопротивление становится комплексным:
где ω - сдвиг по фазе между давлением pa и колебательной скоростью частиц среды v
Для сферической волны модуль акустического сопротивления равен
не превышает акустического сопротивления этой же среды для плоской волны.
Для цилиндрической волны
Разность фаз φ между давлением и колебательной скоростью в сферических и цилиндрических волнах быстро уменьшается с ростом расстояния r и увеличением частоты звука. В дальней зоне (r>>λ) сдвиг фаз φ =0, акустическое сопротивление становится вещественным и равным по величине акустическому сопротивлению среды для плоской волны [1].
Граница раздела двух сред, разделенных тонким слоем
Рассмотрим случай отражения волны от границы двух сред, разделенных промежуточным слоем. Для упрощения будем рассматривать нормальное падение волны, как показано на рис. 2.
Рис.2. Схема прохождения волны на границе раздела двух сред.
Слой имеет толщину h. В нем существуют две волны, распространяющиеся в прямом и обратном направлениях. Из волнового уравнения, с учетом граничных условий задачи (равенство давлений и смещений на обеих границах слоя) можно вычислить амплитуды всех волн. Из них получают следующее выражение для входного импеданса для волны, падающей на слой сверху (мы рассматриваем только продольные волны).
где ρc - плотность слоя;
cc - скорость продольной волны;
Z2 - импеданс среды в которую переходит волна.
Акустические импедансы контактных сред или их отношение является основной исходной величиной для расчетов прозрачности границы раздела сред и коэффициента отражения акустической волны.
Комплексное значение входного импеданса означает, что давление и колебательная скорость не совпадают по фазе. Сдвиг фазы происходит в результате многократных отражений волн в слое. Если среда в которую переходит волна протяженная, то Z2=ρccc. Зная Zin, мы можем вычислить коэффициенты отражения и акустической прозрачности, используя следующие выражения:
Здесь вместо ![]() поставили Zin , т. к. оно является результатом суммирования всех действующих волн. Аналогично коэффициент прозрачности
поставили Zin , т. к. оно является результатом суммирования всех действующих волн. Аналогично коэффициент прозрачности
Т. к. Zin зависит от hc, то и коэффициенты R и D также будут зависеть от hc.
Для реальных материалов, обладающих свойством затухания, амплитуда осцилляции коэффициентов отражения и прозрачности убывает с увеличением hc. Поэтому для получения максимального эффекта следует брать слой минимальной толщины, а именно ![]() [3].
[3].
Практическая реализация
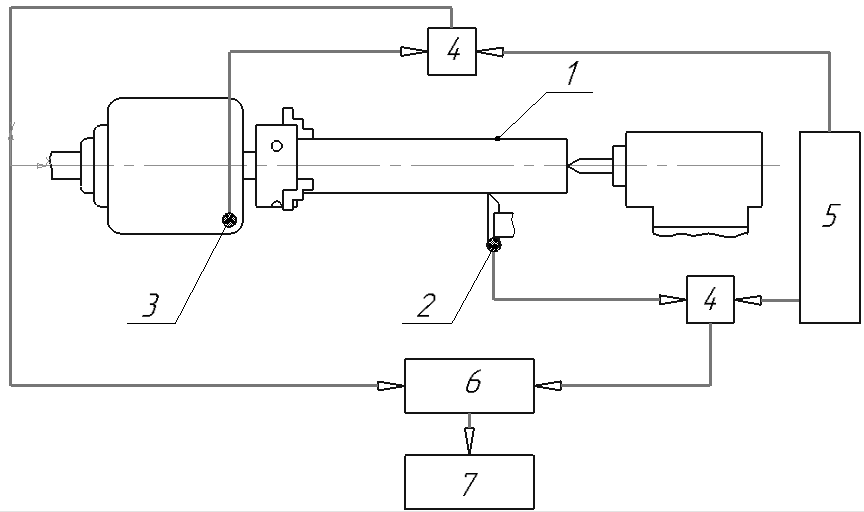
В результате проделанных работ был проведен глубокий анализ научных материалов, что позволило создать стенд определения параметров виброакустического тракта автоматической системи технической диагностики (АСТД). Схема стенда приведена на рис. 3
Рис.3 Схема стенда определения параметров механической части виброакустического тракта АСТД
На схеме номерами обозначены:
1 – деталь;
2 – датчик, установленный в опорной точке;
3 – датчик, установленный в измерительной точке;
4 – усилитель сигнала;
5 – блок питания системы;
6 – аналого-цифровой преобразователь (АЦП);
7 – персональная электронно-вычислительная машина (ПЭВМ).
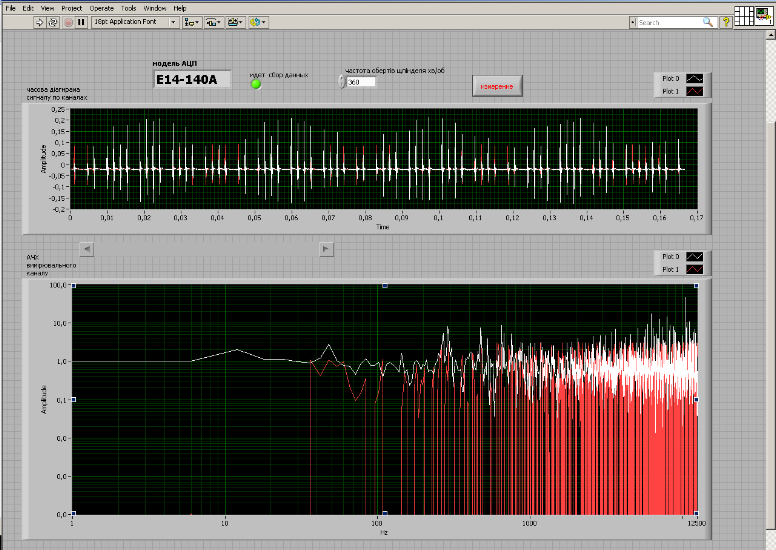
Работа стенда обеспечивается созданной программой, предназначенной для построения амплитудно-частотных и фазо-частотных характеристик (АЧХ и ФЧХ) механической части акустического тракта. Элементы вывода информации представлены двумя графиками (рис. 4.). Первый график: «временная диаграмма виброакустического канала в опорной точке и в точке измерения» – выводит результат измерения действительного сигнала в реальном времени, что снимается измерительной системой соответственно в опорной и измерительной точке. Второй график: «АФЧХ измерительного канала» – выводит обработанный сигнал, а именно амплитудно-фазо частотную характеристику акустического тракта.
Рис.4. Внешний интерфейс программы для построения амплитудно-частотных характеристик.
Суть работы стенда заключается в определении АФЧХ АТ по измерению и анализу разницы между сигналом зашедшим в АТ (опорной точке, поз. 2 рис.3) и сигналом полученным в точке измерения поз.3. Сигнал представляет собой псевдоединичный импульс, созданный технологической системой в следствии перемещении инструмента во время проведения ПМО.
Выводы
Создание математического аппарата описания АТ дает возможность определить оптимальное место установки датчика, исключивши его установку в непосредственной близости к зоне резания. Это позволит решить задачи по внедрению системы технической диагностики качества механообработки и состояния инструмента на основе виброакустического метода.
Библиографический список
- Соловьянова И.П. Теория волновых процессов: Акустические волны: учебное пособие / И.П. Соловьянова, С.Н. Шабунин. – Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2004. – 142 с.
- Кайно Г. Акустические волны: Устройства, визуализации и аналоговая обработка сигналов: Пер. с англ. – М.: Мир, 1990 – 656с.
- Карпанов Б.И. Акустические методы контроля и диагностики. Часть1: учебное пособие / Б.И. Карпанов, М.М. Коротков. – Томск: Изд-во Томского политехнического университета, 2008 – 186с.