Прошло то время, когда эвольвентная передача, составленная из прямозубых цилиндрических колес, была самым технологичным зацеплением. Сегодня весь процесс изготовления зубчатых передач, начиная от теории сопряженных профилей, создания виртуальных моделей, фрезерования на станках с ЧПУ и контроля готовой продукции проходит под управлением компьютерных программ с точностью значительно превосходящей точности традиционных технологий.
Огромный парк специализированных станков и дорогостоящий для них модульный инструмент теперь оказались не востребованными. Результат готовой продукции сопряженных профилей для анализа возможностей проектируемой передачи стал доступным до его изготовления в материале. Беспристрастный объективный оппонент в виде программного обеспечения контролирует полученные данные независимо от желаемых или предполагаемых результатов. Иногда его решения входят в противоречие с классической теорией зацепления [1] или с установившимися правилами проектирования зубчатых передач. Однако опыт прошедших поколений позволяет успешно ориентироваться в возникающих противоречиях при создании новых зацеплений на новых технологиях [2]. Обнадеживает, что «теоретически можно построить зубчатый механизм с самыми различными профилями зубьев» [3, 534].
Прототипом для создания нового радиусного зацепления [4, 64] была принята эвольвентная передача, как самая методически разработанная и широко используемая сегодня в мире. Для определения параметров проектируемого колеса радиусного зацепления в качестве основной единицы была заимствована величина, называемая в эвольвентном зацеплении модулем m [3, 536].
Метод получения сопряженных профилей был создан из второго способа Оливье, который изначально предполагал известным профиль шестерни и передаточное отношение проектируемой передачи. Тогда сопряженный профиль второго колеса получался, как огибающая кривая к последовательным положениям зубьев известного профиля шестерни. Кроме того, известный профиль должен был иметь строгое математическое описание, которое позволяло бы воспроизводить его в любое время с необходимой точностью и привязывать к центру зубчатого колеса с коэффициентом пропорциональности m. Таким профилем боковой поверхности зуба шестерни, привязанным к известному числу зубьев, был принят профиль, состоящий из касательных радиусов головок к касательным радиусам ножек зуба шестерни с их центрами на делительной окружности шестерни (Рис. 1).
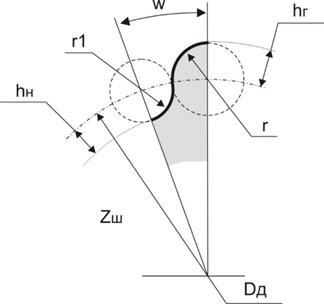
Рис. 1 Боковая поверхность зуба шестерни радиусного зацепления.
На Рис. 1 даны обозначения боковой поверхности зуба шестерни Zш:
r – радиус головки зуба;
r1 – радиус ножки зуба, касательный к радиусу головки зуба r;
hг – высота головки зуба, hг = r;
hн – высота ножки зуба, hн = r1;
Dд – диаметр делительной (начальной) окружности, на котором размещены центры радиусов r и r1;
Zш – известное число зубьев шестерни;
W – угол, охватывающий боковую поверхность зуба шестерни, равный W = 180°/Zш;
m – модуль, с помощью которого традиционно вычисляются остальные параметры зубчатых колес, в том числе r = 0,7854∙m; r1 = m∙Zш∙sin(90°/Zш) – r; Dд = m∙ Zш.
При построении сопряженной поверхности зуба колеса, составляющей с шестерней передачу, в компьютерной программе трехмерного моделирования был использован инструмент создания дуги по трем точкам. Эти точки принадлежали трем последовательным положениям зубьев известного профиля шестерни. Создаваемая огибающая дуга, которая формировала радиус головки зуба колеса касательный к радиусу ножки зуба колеса, проходила через эти три точки. Радиус ножки зуба колеса при этом был равен радиусу головки зуба шестерни (Рис. 2).
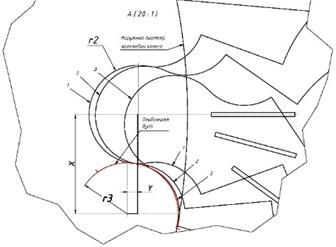
Рис. 2. Огибающая к последовательным положениям зуба шестерни
Таким образом, была создана цилиндрическая радиусная передача, геометрия зубьев которой состояла из касательных радиусов (Рис.3).
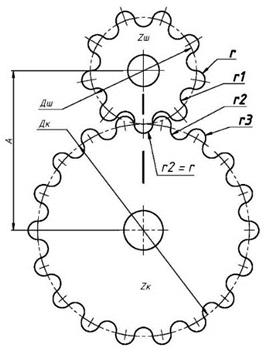
Рис. 3 Цилиндрическая радиусная передача
Полученная радиусная передача преодолела недостатки эвольвентного зацепления по ограничению числа зубьев (Рис.4),

Рис. 4 Шестерня с числом зубьев 9
по увеличению длины рабочего участка линии зацепления (Рис. 5),

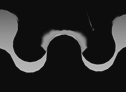
Рис. 5 Напряжение зуба шестерни при передаче крутящего момента на угол поворота от 0°до 18°.
по отсутствию интерференции внутреннего зацепления с разностью в один зуб (Рис. 6),
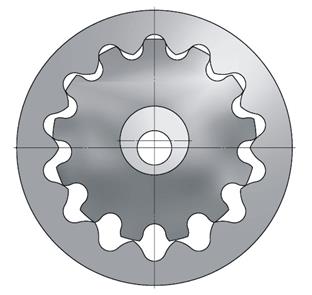
Рис. 6 Внутреннее зацепление с разностью в один зуб
Компьютерное моделирование напряжений в радиусном зацеплении при передаче крутящего момента наглядно продемонстрировало преимущества нового зацепления.
Например, крутящий момент в радиусном зацеплении передается почти всей стороной зуба (Рис. 5), а не только его частью, как в эвольвентном зацеплении.
Во внутреннем радиусном зацеплении с разностью в один зуб отсутствует интерференция и при этом усилия воспринимают одновременно несколько зубьев (Рис. 7).
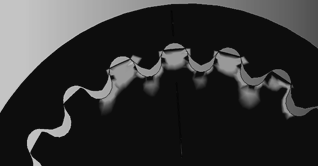
Рис.6 Напряжение во внутреннем зацеплении
Уменьшение кинематической погрешности радиусного зацепления поддерживается расчетной точностью заданных величин по передаточному отношению, в то время как в эвольвентном зацеплении она является производной величиной от точности взаимодействия между собой эвольвентных профилей. А эвольвентные профили зубьев цилиндрических колес, как было показано [2], не дают постоянства передаточного отношения в процессе контакта между собой.
Радиусное зацепление было реализовано в Московском научно-исследовательском телевизионном институте ЗАО «МНИТИ» при создании нестандартного оборудования (Рис.7).

Рис.7 Фрагмент привода радиусного зацепления нестандартного оборудования
Библиографический список
- Бабичев Д. Т., Волков А. Э. История развития зубчатых передач // Вестник научно-технического развития. 2015. №5. С. 25-42.
- Пахомов С.Н. Программное обеспечение – инструмент разрешения споров //САПР и графика. -2014.- №8. – С. 104-105.
- Артоболевский И.И. Теория механизмов. – М.: Наука. 1967. стр. 719.
- Пахомов С.Н. Эвольвента – что платье для голого короля // Наукоемкий бизнес. 2015. №1. – С. 62-66.


