«Теоретически можно построить зубчатый механизм с самыми различными профилями зубьев». На практике выбор очертания зубьев в значительной степени зависит от технологии их изготовления [1, 534]. Однако с возникновением компьютерного моделирования и технологии прототипирования на 3D принтерах [2] практически сняты все ограничения по созданию современных зубчатых передач. Естественно возникает вопрос, какие же должны быть современные зубчатые передачи, если даже «классическая теория зацеплений не во всем отвечает высоким требованиям компьютерного проектирования» [3, 37]. Между тем, ученые МГТУ им. Н.Э. Баумана вынуждены констатировать, что «относительная масса зарубежных редукторов в среднем в два раза меньше редукторов отечественного производства» [4, 6].
Определить пути ликвидации отставания отечественных редукторов в современных условиях – цель данной статьи. Опираясь на исторический опыт создания зубчатых зацеплений, и учитывая, возможности новых технологий, можно все-таки потеснить традиционные эвольвентные передачи, которые, несмотря на известные недостатки, продолжают доминировать в мире с 80% среди всех зацеплений [3, 29].
Основной задачей профилирования зубьев круглых колес считается получение таких их очертаний, которые при взаимодействии между собой реализуют постоянство передаточного отношения. С этой целью можно воспользоваться вторым способом Оливье, исходной информацией для которого, являются заданный профиль зуба одного колеса и известное передаточное отношение, которое необходимо реализовать проектируемой передачей. Тогда сопряженный профиль зуба другого колеса будет огибающей к последовательным положениям заданного профиля зуба [3,29].
Кроме того, известный профиль, привязанный к заданному числу зубьев, должен иметь строгое математическое описание, которое позволяло бы воспроизводить его в любое время с необходимой точностью с коэффициентом пропорциональности, называемым в эвольвентном зацеплении модулем m.
Для исследования возможностей нового зацепления было выбрано радиусное зацепление [5]. Характерными его особенностями являлись касательные радиусы, которые строили боковые поверхности зубьев шестерни и колеса. В каждом колесе радиусы головок зубьев отличались от радиусов ножек зубьев. В шестерне радиусы головок были больше радиусов ножек зубьев. В колесе, составляющей с шестерней пару, радиусы ножек зубьев были равны радиусам головок зубьев шестерни. Радиусы головок зубьев колеса отличались от радиусов ножек зубьев колеса. Радиусы головок зубьев колеса были представлены участком кривой, который строился компьютерным моделированием в виде огибающей окружности. Центры всех радиусов, кроме радиусов головок зубьев колеса, размещались на делительных окружностях шестерни и колеса. Это позволяло зубчатые венцы шестерни и колеса представлять плавными кривыми, состоящими из сопряженных профилей зубьев, которые заставляли делительные окружности шестерни и колеса обкатываться друг по другу без скольжения.
Из эвольвентного зацепления было известно, что «Никаких заранее определенных углов зацепления, линий зацепления, полюсов, начальных окружностей и высот головок и ножек у отдельно взятого эвольвентного зубчатого колеса не существует; они определяются только при зацеплении двух колес» [6, 415]. Это в полной мере относится и к радиусному зацеплению, например, внутреннего зацепления с разностью в один зуб (Рис. 1).
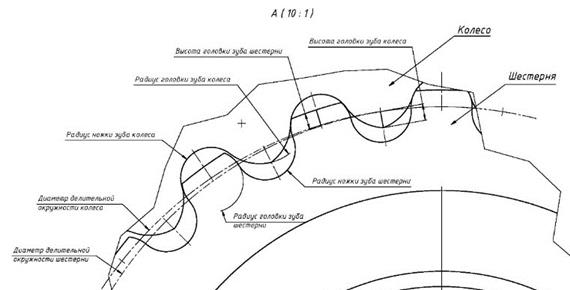
Рис. 1 Радиусное зацепление внутреннее
Теперь, когда были сняты ограничения производства, в плену которых находилось эвольвентное зацепление:
1. по минимальному числу зубьев в передаче (Рис. 2);

Рис. 2 Шестерня на оси двигателя с числом зубьев 9
2. по фрезерованию наружного и внутреннего зацеплений на станках ЧПУ (Рис. 3);
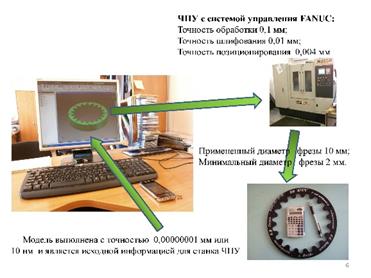
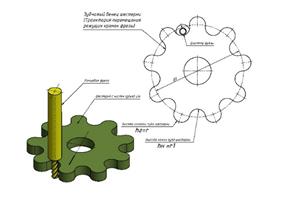
Рис. 3 Нарезание радиусных зубчатых колес на станке с ЧПУ
3. по внутреннему цилиндрическому зацеплению, с разностью в один зуб (Рис. 4);

Рис.4 Внутреннее зацепление с разностью в один зуб
4. по проектированию внутреннего конического зацепления с разностью в один зуб (Рис. 5)
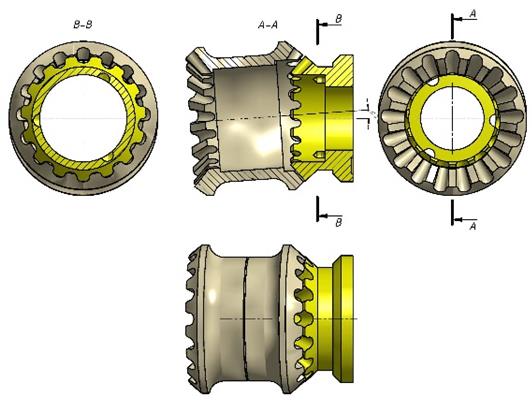
Рис. 5 Компьютерная модель деталей, которые имеют внутреннее коническое зацепление
предстояло, оглянувшись назад, попытаться создать такие схемы механизмов, которые до этого были недоступны эвольвентному зацеплению и на их основе, реализовать высокий коэффициент относительной массы отечественных изделий.
Одним из параметров совершенства зубчатого механизма является его КПД. Хорошо известно, что «чем меньше в механизме работа непроизводственных сопротивлений, тем меньше его коэффициент потерь и тем совершеннее механизм в энергетическом отношении» [1, 389]. «Мощность в зацеплении характеризует возможные потери в механизме. Чем больше эта мощность, тем больше потери и тем, следовательно, ниже коэффициент полезного действия» [1, 401].
Мощность в зацеплении, затрачиваемая на трение скольжения в зубьях, определяется уравнением [1, 396]:
N= f∙P 12∙υcк в котором:
f – Коэффициент скольжения трения, зависимый от материалов зубьев,
P 12 – давление зуба шестерни на зуб колеса,
υcк – величина скорости скольжения зубьев друг по другу.
Известно, что КПД некоторых механизмов планетарных передач, относящихся к силовым передачам, выше рядовых. Если в рядовых передачах потери характеризуются коэффициентом трения скольжения f [1, 302], то планетарную передачу, можно представить фрикционным механизмом с коэффициентом трения качения к [1, 298] (Рис. 6).
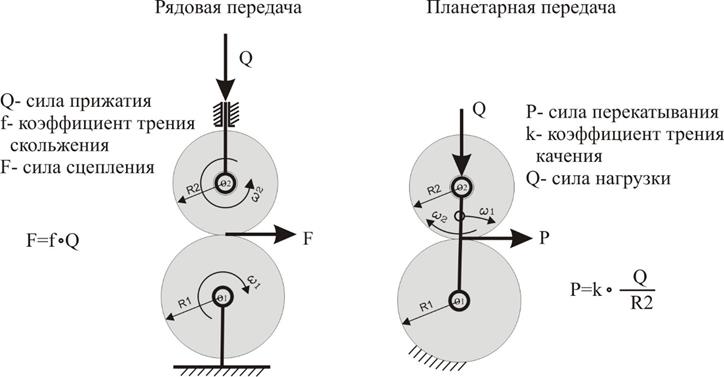
Рис.6 Сравнение рядовых и планетарных передач
При одинаковых нагрузках Q сила трения F во фрикционном механизме с неподвижными осями значительно больше силы перекатывания P планетарного механизма. Из этого можно сделать первый вывод: В основу схем перспективных механизмов с высоким КПД должны быть взяты схемы силовых планетарных передач.
К силовым передачам относятся такие планетарные механизмы, у которых реакции R1, R2 на сателлитах z1, z2 от внешнего момента расположены по разные стороны от осей этих сателлитов (Рис. 7) [7].
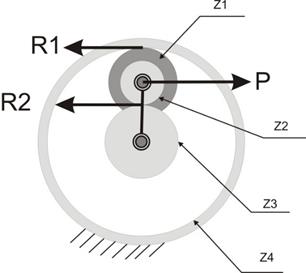
Рис. 7 Реакции на сателлите от внешнего момента
Второй вывод касается преимущественного применения в новых разработках внутреннего зацепления, так как в нем, кроме других преимуществ, меньше скорости скольжения зубьев υcк , которые пропорционально влияют на мощность в зацеплении [8].
Параметром, определяющим степень совершенства зубчатого механизма, является передача крутящего момента, при минимально возможном их весе. Именно по относительной массе происходило сравнение редукторов отечественного производства с их импортными аналогами [4,6].
В свою очередь, относительная масса зависит от кинематической схемы механизма. Состоящие не более, чем из четырех колес, планетарные схемы способны реализовать почти весь востребованный промышленностью диапазон передаточных отношений (Рис. 8).
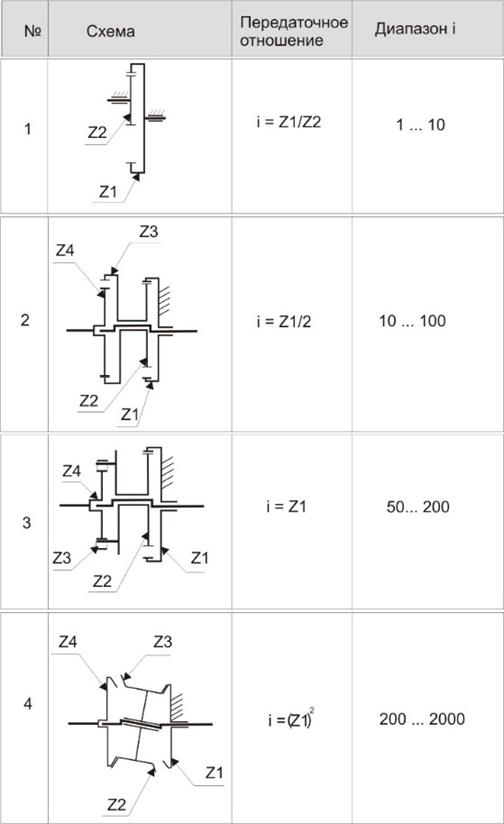
Рис. 8 Таблица вариантов кинематических схем, перекрывающих
востребованный диапазон передаточных отношений
Так редуктор Рис. 9, спроектированный по схеме №2 из таблицы Рис. 8, имел коэффициент технического уровня в три раза лучше, чем самый совершенный планетарно-цевочный редуктор Японского производства.
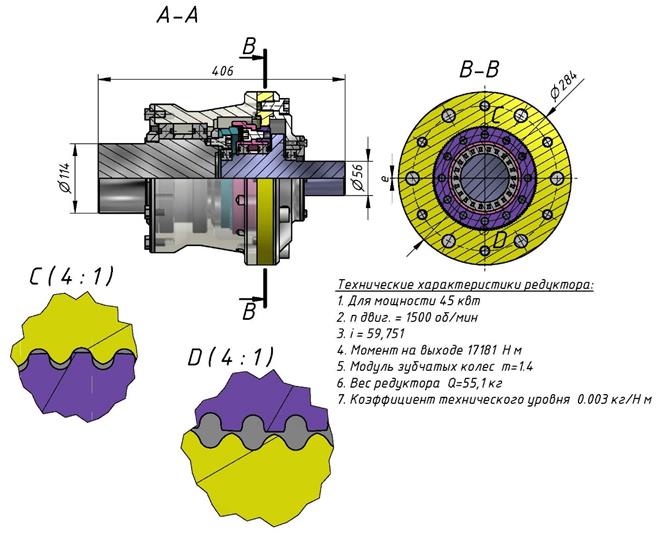
Рис. 9 Редуктор с колесами радиусного зацепления
Вывод:
Создана таблица вариантов кинематических схем механизмов радиусного зацепления во всем диапазоне востребованных передаточных отношений, по которой можно проектировать редуктора по техническому уровню превосходящие зарубежные.
Библиографический список
- Артоболевский И.И. Теория механизмов. – М.: Наука. 1967. стр. 719.
- CUBICPRINTS // Материалы для 3Д-печати: характеристики и цены [Электронный ресурс]. – Режим доступа: http://www.cubicprints.ru/materials.
- Бабичев Д. Т., Волков А. Э. История развития зубчатых передач // Вестник научно-технического развития. 2015. №5. С. 25-42.
- А.С. Иванов, С.В. Маркин Конструирование современных мотор-редукторов. Электронное учебное издание. М.: МГТУ им. Н.Э. Баумана, 2012.
- Пахомов С.Н. Программное обеспечение – инструмент разрешения споров //САПР и графика. -2014.- №8. – С. 104-105.
- Краткий справочник машиностроителя. Редакция С.А. Чернавского. – М.: Машиностроение, 1966. стр. 797.
- Пахомов С.Н. Об одной планетарной схеме привода для специального телевидения// Техника средств связи. Серия техника телевидения. М.: МНИТИ, 2011. С. 120-124.
- Кирютин А.С. Анализ способов и применяемого зуборезного инструмента для обработки колес внутреннего зацепления с эвольвентным профилем // Современная техника и технологии. 2014. № 3 [Электронный ресурс]. URL: http://technology.snauka.ru/2014/03/3332 (дата обращения:13.11.2015).


