Рассмотрим нестационарную эргатическую систему, описываемую уравнением:

, .

(1)

Формирование у оператора требуемых навыков управления в условиях тренажера связано с его имитационными характеристиками. Эта задача не может быть решена без параметрической идентификации, как объекта управления рассматриваемой эргатической системы, так и модели объекта. Только после этого имитационные характеристики определятся на основе сравнения параметров реального объекта и его модели. 
Ограничимся рассмотрением частной задачи параметрической идентификации объекта для короткопериодической составляющей продольного движения. Уравнения движения имеют вид [1]:

, .

(2)

Учитывается зависимость управляющих воздействий оператора от собственной частоты колебаний объекта управлений [2]. Известно, чем лучше оператор приспособился к объекту управления, тем больше дисперсия, приходящаяся на диапазон  в спектральной плотности управляющих воздействий оператора (принято ). 
Рассмотрим интервал  реализаций = (, ); , . Предполагается, что на интервале  элементы матриц  меняются мало. Тогда на интервале задача сведется к определению 
по синхронным измерениям ; - вектор состояния,  - одномерный вектор управления.
В дискретной форме уравнение (1) имеет вид:

, ;

(3)

,
.

Введем

, ,
, .

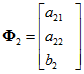Уравнение (3) сведется к виду

.

(4)

Действительно,

,
.

Откуда с учетом

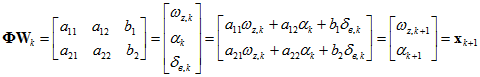
получим

,
,

где

 ,;

в скобках указаны моменты -го замера  и . Число r должно быть больше идентифицируемых параметров. Матрица  определяется в виде:

.

Справедливо

.

Тогда  - -матрица, откуда следует, что - -матрица. Поэтому  есть -матрица. В связи с чем ,  - есть -матрица, то есть вектор-столбец.
Таким образом,

=, =.

Алгоритм идентификации включает обращение матрицы третьего порядка (предполагается существование обратной матрицы). Естественно, использование методики возможно только для центрированных процессов (учтено в уравнении (1): управляющие воздействия оператора рассматриваются как отклонения от программного движения (тренд)).
Далее. Пусть для каждого -го интервала ,  определены оценки  и  по приведенной выше методике. Тогда по их дискретным значениям можно получить приближенные аналитические выражения для функций . Можно воспользоваться, например, полиномами Ньютона

,
;
.

Коэффициенты  и  определятся через конечные разности функций  соответственно.
Рассмотренный алгоритм использовался при идентификации нестационарного продольного движения [3…7]; точность идентификации определялась с использованием системы с известными коэффициентами: на вход подавались массивы точного решения при разных интервалах дискретизации (составила 14% ).

1. Авиационные тренажеры модульной архитектуры: монография; под редакцией Лапшина Э.В., д.т.н., проф. Данилова А.М. – Пенза: ИИЦ ПГУ.  – 2005.  – 146 с.
2. Данилов А.М., Гарькина И.А., Домке Э.Р. Математическое моделирование управляющих воздействий оператора в эргатической системе / Вестник МАДИ. – 2011. –№2.  – С.18-23.
3. Гарькина И.А., Данилов А.М., Петренко В.О. Решение приближенных уравнений: декомпозиция пространственного движения управляемого объекта // Современные проблемы науки и образования. – 2014. – № 5; URL: http://www.science-education.ru/119-14766
4. Гарькина И.А., Данилов А.М., Прошин И.А. Тренажеры модульной архитектуры для подготовки операторов транспортных систем / XXI  век: итоги прошлого и проблемы настоящего (плюс) Серия: технические науки. Машиностроение и информационные технологии. – №12(16). – 2013. –С. 37-42.
5. Будылина Е.А., Гарькина И.А., Данилов А.М., Пылайкин С.А. Аналитическое определение имитационных характеристик тренажных и обучающих комплексов // Фундаментальные исследования. – 2014. – № 6 (часть 4). – С. 698-702.
6. Будылина Е.А., Гарькина И.А., Данилов А.М. Приближенные методы декомпозиции при настройке имитаторов динамических систем / Региональная архитектура и строительство.   –  2013.  – № 3.  – С. 150-156.
7. Будылина Е.А., Гарькина И.А., Данилов А.М. Приближенные методы декомпозиции при настройке имитаторов динамических систем / Региональная архитектура и строительство.   –  2013.  – № 3.  – С. 150-156.

Все статьи автора «fmatem»