Многие виды автомобильной техники, такие как: автомобили с установленными на них кранами, снегоуборочные машины, машины для транспортировки мусорных контейнеров, мусоровозы, тракторы с навесными орудиями, дорожностроительные машины и т.д, – оснащены гидроцилиндрами различных видов и размеров. Также широко используются в различных механизмах и пневмоцилиндры, близкие по конструкции к гидроцилиндрам.
Широкое использование подобных деталей – нежестких деталей класса «полые цилиндры» в разнообразных машинах, устройствах и комплексах вызывает необходимость изготовления этих изделий в широком диапазоне габаритных размеров – как по диаметрам штоков и отверстий цилиндров, так и по их длинам. 
На основании проведенных ранее исследований [1-3] было отмечено, что комбинированная обработка нежестких деталей класса «полые цилиндры» резанием и поверхностным пластическим деформированием с помощью специальных устройств (для комбинированной обработки) дает выигрыш в производительности, высокие показатели точности обработки (8 – 9 квалитет) и хорошую шероховатость обработанной поверхности ().
Однако из-за наличия погрешностей обработки на предыдущих заготовительных операциях, форма обрабатываемой заготовки может иметь погрешности как в продольном, так и в поперечном сечении. Данные погрешности негативно влияют на точность комбинированной обработки рассматриваемых деталей, поскольку вызывают изменение глубины резания, в результате чего изменяется сила резания.
В данной статье мы рассмотрим, как глубина резания зависит от погрешности формы обрабатываемой заготовки в поперечном сечении – отклонения от круглости в процессе комбинированной режуще-деформирующей обработки при помощи специального устройства для комбинированной обработки, конструкция которого подробно описана в [1].
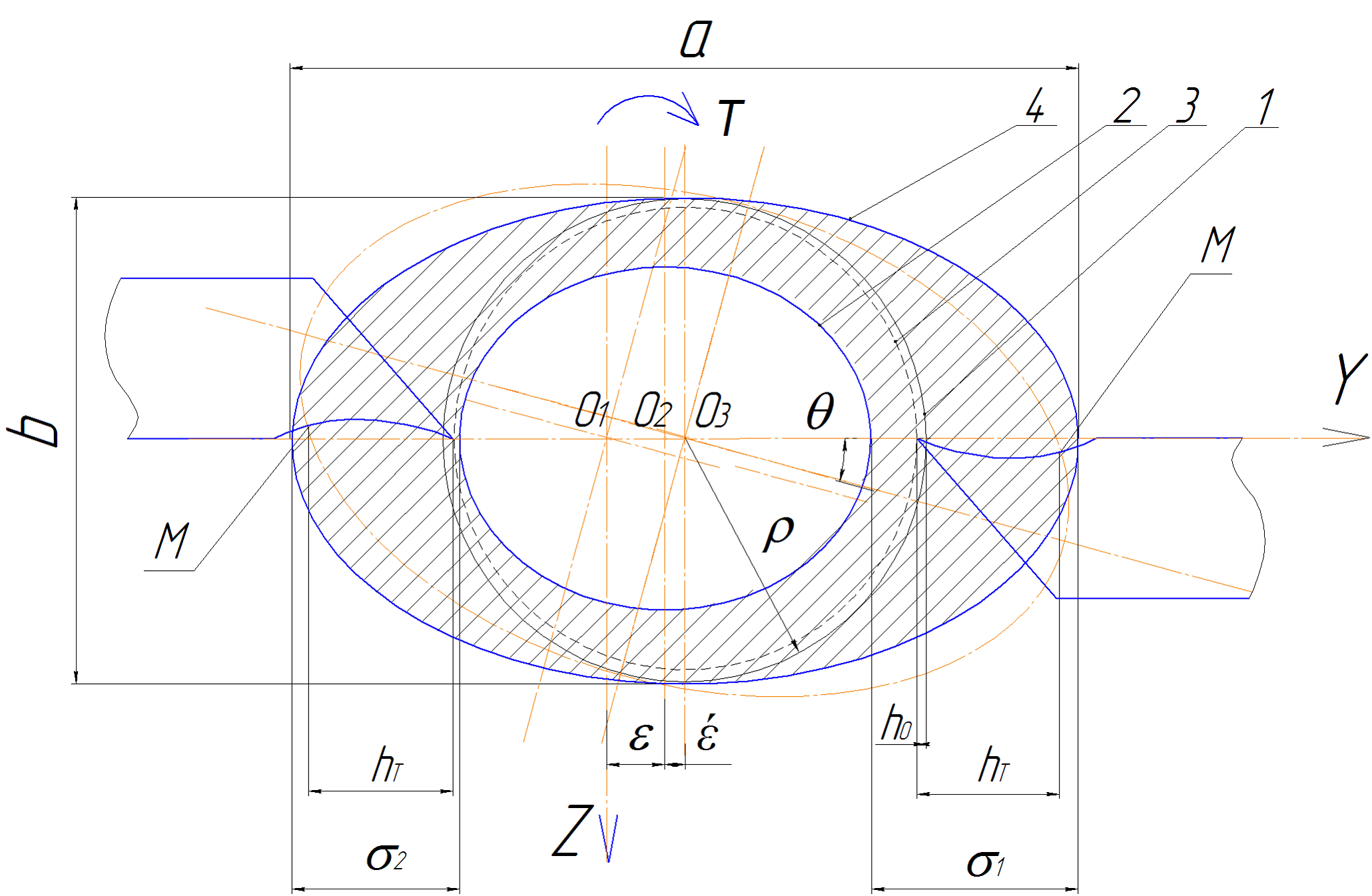
Под воздействием поперечной (назовем ее перерезывающей) силы, вызываемой резцовым блоком данного устройства для комбинированной обработки, происходит деформация поперечного сечения обрабатываемой заготовки, которая поступила на комбинированную обработку уже с погрешностями, полученными на предыдущих заготовительных операциях. Вследствие этого данное поперечное сечение представляет собой не кольцо в некоторой точке с координатой Х по длине, а может быть представлено двумя неконцентричными эллипсами, как показано на рисунке 1.

На данном рисунке 1 изображено сечение заготовки с уже имеющимися погрешностями в поперечном сечении – эксцентриситетом, концентричностью и разнотолщинностью. Цифрой 1 обозначен наружный контур идеальной заготовки, цифрой 2 – контур внутреннего отверстия заготовки, цифрой 3 – наружный контур готовой детали и цифрой 4 обозначен наружный контур реальной заготовки с уже имеющимися погрешностями в поперечном сечении. Переменными и  обозначена толщина стенок заготовки, при этом величина допуска на толщину стенки , - радиус идеальной заготовки с контуром 1,  - угол поворота заготовки в процессе обработки.
Поскольку базирование рассматриваемой детали происходит по поверхностям, формируемым относительно наружной поверхности, и обработка ведется тоже по наружной поверхности (схема комбинированной обработки представлена в [1]), то погрешность разнотолщинности  в известной мере не оказывает влияния на изменение глубины резания, а влияет только лишь на колебания поперечного сечения детали в процессе обработки. Поэтому далее будем рассматривать только наружный эллипс.
Полуоси наружного эллипса -  и , причем . Ось  – линия центров станка, ось  - ось внутреннего эллипса, ось  - ось наружного эллипса, является осью обрабатываемой детали. - величина отклонения от концентричности наружного и внутреннего эллипсов,  - величина эксцентриситета. . 
Примем  – заданная глубина резания.
Однако из-за наличия погрешностей в форме заготовки, величины угла поворота заготовки , величины отклонения от концентричности и величины эксцентриситета  реальная глубина резания или текущая глубина резания  будет отличаться от заданной глубины резания .
Текущая глубина резания будет определяться выражением 1:

(1)

где ;
 - угловая скорость вращения заготовки;
 - время обработки;
;
.
С учетом вышеизложенного выражение 1 примет вид:

(2)

Изменение глубины резания происходит также и вследствие изогнутости оси обрабатываемой нежесткой заготовки, вызванной изгибными колебаниями, причем изменение глубины резания на резцах равно по величине и противоположно по знаку [1], а также вследствие деформации поперечного сечения заготовки под воздействием перерезывающей силы. Обрабатываемая заготовка вращается с угловой скоростью, ось детали, как указано выше, отклонена от оси ОХ в сечении Х на величину поперечного перемещения, вызванного поперечными или изгибными колебаниями – величину прогиба, которую обозначим как .
Пусть первоначальная (исходная) деформация поперечного сечения заготовки под воздействием перерезывающей силы будет обозначена  (мм), тогда величина деформации поперечного сечениязаготовки, вращающейся со скоростью , может быть описана выражением 3:

(3)

где  - начальный угол поворота поперечного сечения нежесткой заготовки; 
 - дельта-функция по координате.
Рассмотрим первоначальную деформацию поперечного сечения заготовки под воздействием перерезывающей силы - . В начальный момент времени  в точке  имеют место лишь собственные свободные колебания поперечного сечения. 
Задача решается 2 раза при следующих граничных условиях: в начальный момент времени  в точке  первоначальная деформация  равна 0; и в начальный момент времени  в точке первоначальная деформация  максимальна и составляет . Граничные условия в начальный момент времени тогда можно записать в виде (4):

(4)

Величину  можно найти из задачи свободных колебаний поперечного сечения [4]. Примем следующие допущения. Во-первых, поперечное сечение заготовки будет представлено в виде кругового кольца постоянного поперечного сечения в предположении, что размеры поперечных сечений данного кольца малы в сравнении с радиусом осевой окружности, и что каждое поперечное сечение имеет ось симметрии, расположенную в плоскости кольца. Во-вторых, величина прогиба зависит только от толщины стенки заготовки, и радиусом рассматриваемого кольца мы будем считать усредненную линию между максимальной и минимальной толщиной стенки (или же усредненную линию от минимальной толщины стенки, ведь только там будет происходить максимальная деформация в начальный момент времени). В данном случае нас интересуют радиальные колебания поперечного сечения заготовки. В этом случае осевая линия кольца представляет окружность с периодически изменяющимся радиусом, как показано на рисунке 2, и все поперечные сечения движутся в радиальных направлениях без поворотов.
На рисунке 2 приняты следующие обозначения: - радиус осевой линии недеформированного кольца, - радиальное перемещение, принятое положительным по направлению к центру и одинаковое для всех поперечных сечений, - площадь поперечного сечения кольца. - деформация кольца по оси ,  - деформация кольца по оси . Тогда относительное удлинение кольца в окружном направлении будет обозначено как .

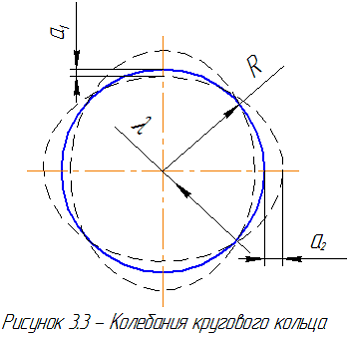
Рисунок 2 – Колебания кругового кольца

Потенциальная энергия деформации, состоящая в нашем случае из энергии простого растяжения, определяется выражением:

(5)

где: - модуль упругости материала обрабатываемой заготовки.
Кинетическая энергия колебаний равна:

(6)

где:  - ускорение силы тяжести;
 - вес единицы объема материала обрабатываемой заготовки.
Из выражений 5 и 6 получаем:

(7)

Откуда далее можно получить гармоническое (колебательное) движение кольца:

(8)

где: ;
 - произвольные постоянные интегрирования, для определения которых нужно рассмотреть начальные условия. В начальный момент времени . 
Подставим  в выражение 8, откуда получим:

(9)

Далее продифференцируем выражение 8 по времени и подставим  в выражение производной, получаем:

(10)

В начальный момент времени деформация кольца по оси  -  нас не интересует, поскольку в начальный момент времени резцы резцового блока устройства для комбинированной обработки [1] расположены по оси . Поэтому ограничимся рассмотрением величины - деформации кольца по оси . Это и будет величина . Эту величину можно представить в виде:

(11)

Итак, изменение глубины резания, вызванное изогнутостью оси обрабатываемой заготовки, т.е. изгибными колебаниями, а также деформацией поперечного сечения заготовки, можно описать выражением 12:

(12)

Таким образом, просуммировав указанные выше изменения глубины резания и учитывая, что реальная глубина резания может быть описана выражением:

(13)

где:  – текущая глубина резания;
 - погрешность, вносимая передним центром устройства для комбинированной обработки;
На основании выражения 13 можно получить выражение 14, по которому будет определяться реальная глубина резания:

(14)

где:  – частота вращения заготовки.

На основании вышеизложенного можно сделать вывод, что глубина резания в процессе обработки зависит от погрешностей геометрии поперечного сечения нежестких деталей класса «полые цилиндры». При изменении глубины резания изменяется и сила резания, что негативным образом влияет на параметры точности комбинированной обработки деталей данного класса.

1. Анкин А.В. Повышение производительности и качества комбинированной обработки нежестких валов. Дисс. …  к.т.н.,-  М., МАМИ, 1993.
2. Максимов Ю.В. Исследование условий  обеспечения  качества   обработки нежестких валов.  Дисс.  …  к.т.н.,-  М., МАМИ, 1981, 310 с.
3. Максимов Ю.В. Обеспечение качества и производительности обработки  нежестких  валов  применением технологических систем с дополнительными контурами связи. Дисс.  …  д.т.н.,-  М., МГТУ «МАМИ», 2000.
4. Тимошенко С.П. Колебания в инженерном деле. Издание второе. Главная редакция физико-математической литературы издательства «Наука», 1967.

Все статьи автора «Ветрова Екатерина Андреевна»