УДК 621.313.13

ПОДХОД К ОПТИМАЛЬНОЙ СТРАТЕГИИ ПЕРЕКЛЮЧЕНИЙ ДЛЯ РЕГУЛЯТОРА ТОКА В ОБМОТКАХ ШАГОВОГО ДВИГАТЕЛЯ

Борисевич Алексей Валерьевич¹, Глебко Дмитрий Владимирович²
¹Санкт-Петербургский государственный политехнический университет, доцент кафедры «Автоматы», кандидат технических наук
²Санкт-Петербургский государственный политехнический университет, аспирант кафедры «Автоматы»

Аннотация
Рассматривается задача оптимальной стратегии переключений для релейного трехпозиционного регулятора тока в обмотках шагового двигателя. На основе линейной аппроксимации динамики тока предложена стратегия управления, минимизирующая ошибку регулирования. Приведены результаты моделирования в Matlab Simulink, подтверждающие работоспособность предложенного подхода.

Ключевые слова: Оптимальное управление, регулятор тока, шаговый двигатель

ON OPTIMАL SWITСHING STRАTEGY FOR СURRENT REGULАTOR IN WINDINGS OF THE STEPPER MOTOR

Borisevich Aleksey Valerievich¹, Glebko Dmitriy Vladimirovich²
¹St. Petersburg State Polytechnical University, Ph.D, Associate Professor
²St. Petersburg State Polytechnical University, Ph.D Student

Abstract
The problem of the optimаl strаtegy for the relаy switсhing сurrent сontroller of the stepper motor сonsidered in pаper. Bаsed on а lineаr аpproximаtion of the сurrent dynаmiсs new сontrol strаtegy thаt minimizes the trасking error wаs proposed. The results of simulаtion in Mаtlаb Simulink сonfirmed the effiсienсy of the proposed аpproасh.

Библиографическая ссылка на статью:
Борисевич А.В., Глебко Д.В. Подход к оптимальной стратегии переключений для регулятора тока в обмотках шагового двигателя // Современная техника и технологии. 2015. № 3 [Электронный ресурс]. URL: https://technology.snauka.ru/2015/03/5935 (дата обращения: 01.05.2025).

Стабилизация тока в обмотках шагового двигателя – задача, которая решается в любом контроллере независимо от его режима работы.

В настоящей работе рассматривается задача трехпозиционного регулирования тока в обмотках, известная как режим смешанного спада тока (mixed decay mode) [1]. Многие серийно выпускаемые интегральные драйверы шаговых двигателей реализуют данный режим управления, например A3986, A4975 фирмы Allegro или LB11847 фирмы On Semiconductor [1,2].

1. Алгоритм контроллера тока

Типичный алгоритм работы релейного контроллера тока можно описать следующим образом.
Пусть задана уставка тока $i_{ref}$ . Сигнал с датчика (резистивного шунта) известен как $i(t)$ . Как только реальный ток становится больше заданного $i(t) \ge i_{ref}$ , то контроллер выключает питание обмотки на фиксированное время $\tau_{off}$ .

Режима смешанного спада тока основывается на том, что отключение обмотки шагового двигателя с помощью мостовой драйвера может быть выполнено двумя путями: циркуляцией тока через открытый транзистор противоположного плеча или через обратные диоды транзисторов моста (рисунок 1). В первом случае реализуется т.н. режим медленно спадающего тока (slow decay mode), во втором случае – режим быстро спадающего тока (fast decay mode). Предположим, что обмотка была подключена к источнику питания, и ток в ней достиг заданного уровня. После чего релейный регулятор тока отключает обмотку на время $\tau_{off}$ . В режиме смешанного спада тока сначала активируется быстрый спад на фиксированное время $\tau_f$ , а потом – медленный спад на интервале времени от $\tau_f$ до $\tau_{off}$ .

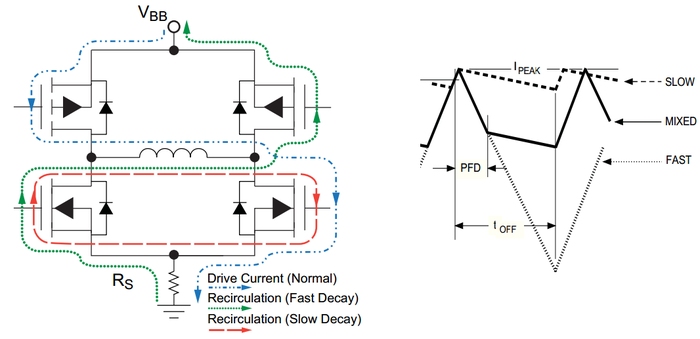
Рисунок 1. Быстрый (fast), медленный (slow) и смешанный (mixed) спад тока.

2. Процессы переключения между быстрым и медленным спадом тока

Пусть значение уставки тока уменьшается $d i_{ref}(t)/dt \le 0$ . Проанализируем каким образом осуществляются переключения в режиме смешанного спада тока. Пусть в некоторый момент времени $t_0$ произошло отключение обмотки после того, как $i(t) = i_{ref}$ . Без потери общности, положим для упрощения анализа, что $i_{ref} = 0$ , а также $t_0 = 0$ .

Предположение 1. На интервале времени выключения $[t_0,~ t_0 + \tau_{off}]$ токи $i(t)$ и $i_{ref}(t)$ изменяются линейно.

Обозначим линейную скорость уменьшения уставки тока $i_{ref}$ на интервале $[t_0,~ t_0 + \tau_{off}]$ :

$k_r = -\frac{d i_{ref}}{d t}, ~ i_{ref}(t) = -k_r \cdot t$ .

Пусть также $k_f$ – скорость уменьшения тока в режиме быстрого спада, $k_s$ – скорость уменьшения тока при медленном спаде.
Введем в рассмотрение переменную $\eta \in [0,1]$ – отношение длительности быстрого спада тока $\tau_f$ к интервалу $\tau_{off}$

$\eta = \frac{\tau_f}{\tau_{off}}$ .

Отсюда можно записать кусочно-линейную аппроксимацию тока:

$i(t) = \begin{cases} -k_f \cdot t, & t \le \tau_f = \eta \tau_{off}, \\ -k_f \cdot \eta \tau_{off} - (t - \eta \tau_{off}) \cdot k_s, & t \ge \tau_f = \eta \tau_{off}, \end{cases}$ .

Ток на момент окончания периода отключения обмотки $\tau_{off}$ будет равен:

$i(t_0 + \tau_{off}) = \left [ -k_f \eta - (1 - \eta) k_s \right ] \tau_{off}$ .

Введем в рассмотрение рассогласование между уставкой тока $i_{ref}(t)$ и действительным током в обмотке $i(t)$ на момент окончания периода отключения обмотки.

$\Delta = i_{ref}(t_0 + \tau_{off}) - i(t_0 + \tau_{off}) = \left [ k_f \eta + (1 - \eta) k_s - k_r \right ] \tau_{off}$ .

На рисунке 2 показан пример динамики тока при переключении между режимами быстрого и медленного спада.

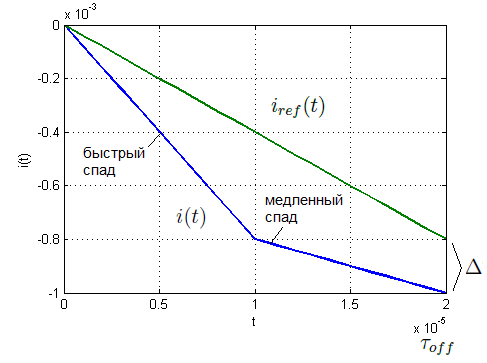
Рисунок 2. Траектория уставки тока и переключение между быстрым и медленным спадом (при $\eta = 0.5$ ).

Утверждение 1. Регулирование тока при спадающем $i_{ref}(t)$ возможно только если

$\Delta \ge 0$ .

Сделанное утверждение понятно после рассмотрения алгоритма работы регулятора. Если ток в обмотке включается всегда после $\tau_{off}$ независимо от того необходимо это или нет, то для непрекращающегося спада тока необходимо выполнение следующего условия для каждого момента $t_0 + \tau_{off}$ включения обмотки:

$i_{ref}(t_0 + \tau_{off}) \ge i(t_0 + \tau_{off})$ .

3. Оптимальное управление

Утверждение 2. Оптимальное управление по критерию

$\int_{t_0}^{t_0 + \tau_{off}} \left ( i_{ref}(t) - i(t) \right)^2 dt \to \min$

достигается при $\Delta = 0$ .

Утверждение очевидно из геометрических соображений (рисунок 2).

Из утверждения 2 следует, что задача оптимального управления по $\eta$ может быть решена как задача стабилизации $\Delta = 0$ , например, с помощью ПИД-регулятора.

Если рассмотреть поведение $\Delta$ на большом количестве периодов переключения, то среднее значение $\bar \Delta$ может быть получено усреднением с помощью фильтра низких частот первого порядка:

$\bar \Delta = PT1_{\tau} [ i_{ref}(t) - i(t) ]$ ,

где $PT1_{\tau}[X(s)] = \frac{1}{\tau s + 1} \cdot X(s)$ , $s$ – оператор Лапласа.

Подставляя значение $\Delta$ , получаем динамику в виде

$\bar \Delta = PT1_{\tau} \left [ (k_f - k_s) \eta + k_s - k_r \right ] \tau_{off}$ .

Отбрасывая постоянное возмущение $k_s - k_r$ , получаем в операторном виде модель объекта управления как систему первого порядка:

$\bar \Delta = \frac{k}{\tau s + 1} \eta$ , (1)

где $k = (k_f - k_s) \cdot \tau_{off}$ .

Задача управления системой первого порядка (1) может быть решена с помощью ПИ-регулятора. Пример расчета параметров ПИ-регулятора по коэффициенту усиления $k$ и постоянной времени $\tau$ приведен, например в [3].

4. Моделирование

Для подтверждения работы алгоритмы был проведен ряд численных экспериментов с помощью моделирования в Matlab/ Simulink. Параметры модели двигателя приведены в работе [4].

Представленные ниже результаты описывают моделирование только одной обмотки двигателя. Ток во второй обмотке полагался равным уставке. Регулятор работает с интервалом времени отключения $\tau_{off} = 50$ мкс (20 кГц).

На рисунке 3 показано как регулируется ток в обмотке в режиме медленного спада тока. Как видно, ток в обмотке существенно отклоняется от уставки.

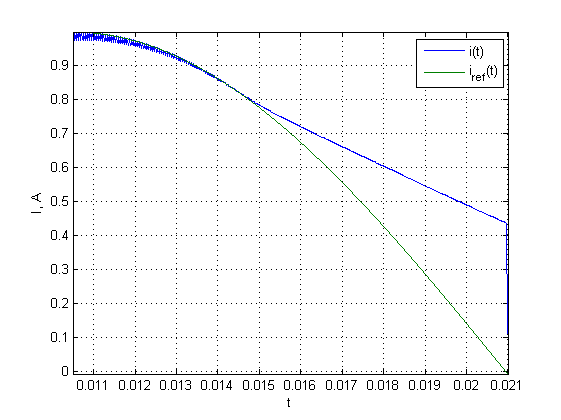
Рисунок 3. Ток в обмотке при фиксированном $\eta = 0$ (только режим медленного спада тока).

На рисунке 4 представлена динамика тока при постоянном соотношении $\eta$ . Как видно, ток имеет существенные пульсации, но в целом следует за уставкой.

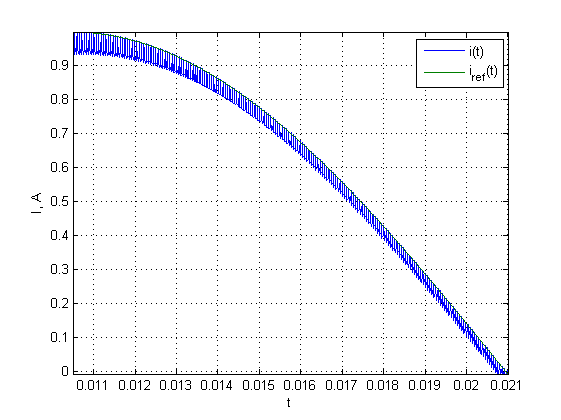
Рисунок 4. Ток в обмотке при фиксированном $\eta = 0.1$ (режим смешанного спада тока).

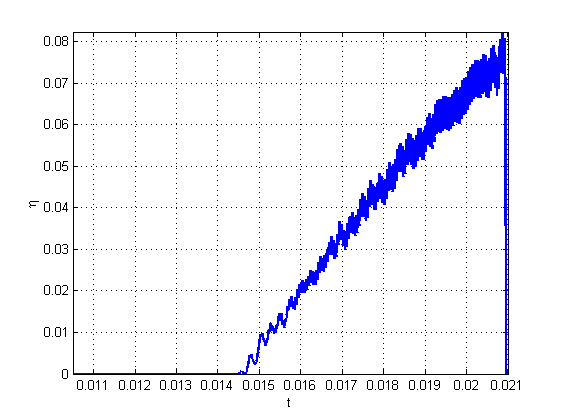
На рисунке 5 представлена динамика тока при предложенном оптимальном управлении для $\eta$ с помощью минимизации рассогласования $\Delta$ . В этом случае, достигаются минимальные пульсации и ток следует за уставкой. Соответствующее этому режиму управление $\eta(t)$ представлено на рисунке 6.

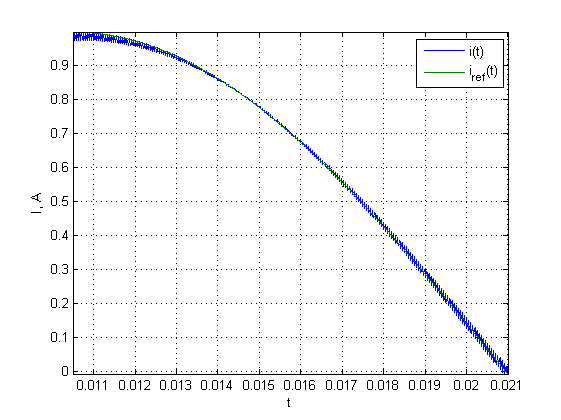
Рисунок 5. Ток в обмотке при оптимальном управлении по $\eta$ .

Рисунок 6. Управление $\eta(t)$ .

Библиографический список

Пушкарёв О. Драйверы шаговых двигателейфирмы Allegro // Современная электроника, декабрь 2004. [Электронный ресурс]. URL: http://www.soel.ru/cms/f/?/311529.pdf (дата обращения: 15.01.2015).
Староверов К. Интегральные решения ON Semiconductor для управления шаговыми двигателями // Новости электроники №5, 2009. [Электронный ресурс]. URL: http://www.compel.ru/lib/ne/2009/5/9-integralnyie-resheniya-on-semiconductor-dlya-upravleniya-shagovyimi-dvigatelyami/ (дата обращения: 15.01.2015).
Борисевич А.В. Автоматическая настройка ПИД-регулятора цифрового термостабилизатора для инкубатора // Современная техника и технологии. 2014. № 6 [Электронный ресурс]. URL: http://technology.snauka.ru/2014/06/4044 (дата обращения: 31.07.2014).
Борисевич А.В., Глебко Д.В. Бездатчиковое векторное управление шаговым двигателем на основе расширенного фильтра Калмана // Современное машиностроение: Наука и образование: Материалы 4-й Междунар. науч.-практ. конференции. / Под ред. М.М. Радкевича и А.Н. Евграфова. – СПб.: Изд-во Политехн. ун-та, 2014. – С. 473 – 484.

Все статьи автора «Борисевич Алексей Валерьевич»

Связь с автором (комментарии/рецензии к статье)

Оставить комментарий

Вы должны авторизоваться, чтобы оставить комментарий.

Если Вы еще не зарегистрированы на сайте, то Вам необходимо зарегистрироваться:

Авторам

О журнале

ПОДХОД К ОПТИМАЛЬНОЙ СТРАТЕГИИ ПЕРЕКЛЮЧЕНИЙ ДЛЯ РЕГУЛЯТОРА ТОКА В ОБМОТКАХ ШАГОВОГО ДВИГАТЕЛЯ

ON OPTIMАL SWITСHING STRАTEGY FOR СURRENT REGULАTOR IN WINDINGS OF THE STEPPER MOTOR

Связь с автором (комментарии/рецензии к статье)

Оставить комментарий