Ставится задача построить схему программного решения cистем уравнений при этом число уравнений и длина промежутка изменения независимой переменной могут быть произвольными. Пусть вначале требуется локализовать и приближенно вычислить все минимумы действительной функции одной действительной переменной 

     (1)

на промежутке  в области ее определения. Строится равномерная сетка: , , . На сетке считываются значения функции (1)

, .      (2)

Элементы массива (2) сортируются. Используется быстрая сортировка, основанная на адресном слиянии двух упорядоченных массивов по матрице сравнений, детально описанная в [1, с. 28]. К выходу сортировки подсоединяется условный оператор, осуществляющий локализацию каждого минимума в окрестности произвольно заданного радиуса  среди элементов (2), при условии, что  меньше половины расстояния между любыми двумя соседними минимумами. Такой оператор можно представить соотношением , . Индексы  входных элементов располагаются на выходе в порядке элементов отсортированного массива. Смысл оператора в том, что в e - окрестности входного элемента с индексом  нет элемента в отсортированном массиве, превосходящего по значению элемент с этим индексом. Данный оператор ниже называется оператором локализации минимума. После локализации минимума выполняется спуск к наименьшему значению в окрестности локализованной точки. Он осуществляется выбором наименьшего значения в сужаемой окрестности c фиксированным числом элементов равномерной сетки, пока не достигается требуемая точность [2, с. 35]. 
Например, все минимумы функции  на отрезке [-30, 30] в результате работы программы, листинг которой представлен в [3, с. 320], примут значения:
-2.67035375557E+0001 -1.00000000000000E+0000
-2.04203522486E+0001 -1.00000000000000E+0000
………………………………………………….
2.98451302089E+0001 -1.00000000000000E+0000
Достигнутая точность приближения характерна для излагаемого метода.
Нули функции идентифицируются как достаточно малые минимумы модулей значений на равномерной сетке. С использованием плоской равномерной прямоугольной сетки схема распространяется на идентификацию нулей функций двух переменных [4, с. 32]. Дискретизированные значения функции интерпретируются как двумерные массивы. Данная схема следующим образом применяется к безусловной численной локализации нулей систем однородных уравнений. Пусть исходная система нелинейных уравнений преобразована к виду однородной системы

      (3)

с действительными левыми частями (как последует из построения, метод распространяется на случай комплексной левой части). Совокупность аргументов  можно рассматривать как n-мерный вектор с действительными компонентами. Аналогично совокупность функций представляет собой такжеn-мерный вектор с действительными компонентами [4, с. 40]. Пусть требуется найти все решения системы (3) в многомерном параллелепипеде, входящем в область ее определения. Строится равномерная сетка, в узлах которой значения канонической нормы вектор-функции из левой части (3) (для определенности норма – сумма модулей компонент) принимаются за элементы массива: 

,       (4)

На вход алгоритма идентификации минимумов функции n переменных подается массив (4), после чего идентифицируются все нули системы (3) как минимумы нормы левой части [4, с. 41]. При этом первоначально идентифицируются все минимумы, затем среди них выбираются те, которые близки к нулю с априори заданной точностью: .
Например, для системы

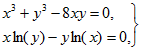
которая имеет три решения, предложенная схема представленная в работе [5, с. 78] дает семь значений минимумов нормы, из них три наименьшие, достаточно близкие к нулю (выделены подчеркиванием), приближают искомые решения:

Схема без изменения применима для приближенных решений систем линейных и нелинейных алгебраических, а также трансцендентных уравнений [4, с. 41], по способу компьютеризации отличаясь от аналогов [6, 7]. На вход метода поступают значения функции, которые с учетом общности ограничений могут вырабатываться в результате решения некоторой другой задачи в реальном времени. Существенным ограничением при этом является требование достаточной малости шага дискретизации. Отличительным качеством, как и в двумерном случае, остается отсутствие начальных приближений, а также области локализации экстремумов, используемых в математических методах [6, 7]. Численный эксперимент показывает применимость схемы в случае вектор-функций из левой части (3) со сложным рельефом [7], включая разрывы первого рода.
Отличительными особенностями предложенного метода являются его построение на основе сортировки, автоматичность программной локализации экстремальных значений функций и систем уравнений, инвариантность схемы относительно размеров области поиска [2, с. 22].

1. Ромм Я.Е. Схемы численной оптимизации на основе алгоритмов сортировки с приложением к идентификации экстремумов решений дифференциальных уравнений. Учебное пособие для студентов вузов, обучающихся по специальности 050202.65 «Информатика» / Я. Е. Ромм, И. В. Заика; М-во образования и науки Российской Федерации, Гос. образовательное учреждение высшего проф. образования «Таганрогский гос. педагогический ин-т». Таганрог, 2010.
2. Ромм Я.Е., Заика И.В. Численная оптимизация на основе сортировки с приложением к поиску нулей и экстремумов решений систем дифференциальных и нелинейных уравнений общего вида. Депонированная рукопись  № 378-В2009 18.06.2009
3. Romm Y.E., Zaika I.V. Numerical sorting-based optimization as applied to general differential and nonlinear equations Romm Y.E., Zaika I.V. Cybernetics and Systems Analysis. 2011. Т. 47. № 2. С. 316-329.
4. Заика И.В., Ромм Я.Е. Метод нахождения экстремумов решений дифференциальных уравнений на основе адресной сортировки. Депонированная рукопись № 908-В2003 12.05.2003
5. Заика И.В., Ромм Я.Е Численное решение нелинейных систем уравнений общего вида на основе алгоритмов сортировки // В сборнике: Научные исследования в современном мире, Материалы Международной (заочной) научно-практической конференции. НИЦ «Наука и образование»; под общей редакцией Д.А. Ефремова. г. Нефтекамск, 2015. С. 78-80.
6. Калиткин Н.Н. Численные методы. – М.: Наука, 1978. -512 с.
7. Березин И.С., Жидков Н.П. Методы вычислений.-Т.2.-М.:Государственное издательство физико-математической литературы, 1962. – 640 с.

Все статьи автора «Леонова Полина Владимировна»