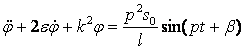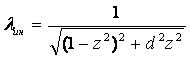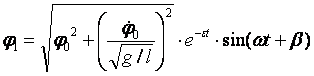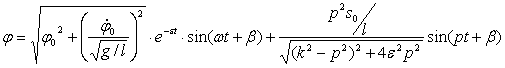ФГБОУ ВПО Волгоградский государственный аграрный университет
В работе обоснованы и определены рациональные параметры датчика положения контейнера на захвате исходя из условий инерционных нагрузок при движении погрузчика по неровностям.
Для хранения и транспортировки сельскохозяйственной продукции довольно часто используются контейнеры, на погрузке и перемещении которых заняты мобильные погрузчики с вилочным захватом. Контроль положения груза на вилочном захвате осуществляется оператором визуально из кабины на удалении от рабочего органа, и при движении погрузчика по наклонной поверхности или переездах через неровности возможно опрокидывание или соскальзывание контейнера с вилочного захвата.
Предлагается на вилочном захвате установить датчик положения маятникового типа [1], заполненный демпфирующей жидкостью, сигнал о наклоне контейнера от датчика поступает на информационную панель в кабину оператора, отображающую наклон к горизонтали вилочного захвата с контейнером. Причём возможен не только визуальный контроль и сигнализация, для принятия решения оператором о выравнивании контейнера, но и введение системы автоматического выравнивания.
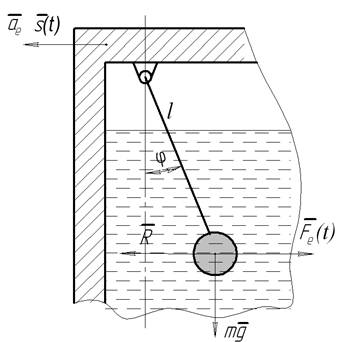
Рассмотрим датчик (рис. 1), имеющий устойчивое положение равновесия, от которого отсчитываем обобщённую координату φ – угол поворота маятника датчика.
Рисунок 1 – Расчётная схема маятникового датчика положения вилочного захвата
В случае инерционного возбуждения маятника датчика при неравномерном движении погрузочного агрегата (разгон или торможение) обобщённая сила Q(t) будет определяться переносной силой инерции Fe(t), т.е.
или с учётом малости угла φ
![]() (2)
(2)
где m – масса маятника, l – его длина.
Дифференциальное уравнение малых колебаний маятника датчика при инерционном возмущении и при наличии диссипативной силы R примет вид
или
где μ – коэффициент демпфирования.
Исходя из допущений о малости колебаний, полагаем cos(φ)=1, sin(φ)=φ, и с учётом выражения (2) после преобразований получим дифференциальное уравнение движения маятника датчика при произвольном инерционном возбуждении, возникающим при движении погрузочного агрегата по неровностям
где 2ε=μ/m, k2=g/l.
Общим решением линейного неоднородного дифференциального уравнения будет
φ=φ1+φ2.
(6)
Составляющая собственных колебаний маятника при наличии вязкого сопротивления определится
Для исключения амплитудных искажений маятникового датчика необходимо чтобы частота собственных колебаний прибора k значительно превышала максимальную частоту учитываемых гармоник периодически измеряемой величины p, а для исключения фазовых искажений необходимо, чтобы фазовые сдвиги были близки к нулю [2]. Для этого прибор должен иметь как можно большую добротность Д=1/d и соответственно как можно меньший безразмерный коэффициент затухания.
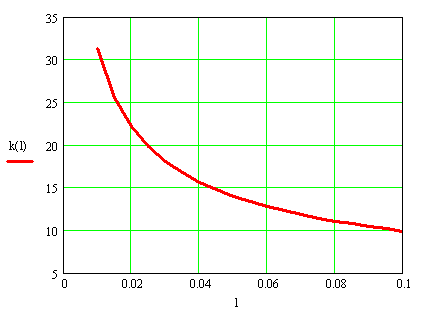
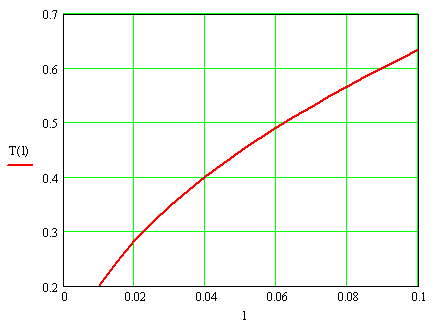
Для маятникового датчика основным параметром влияющим на его собственную частоту и период колебаний будет длина подвеса l, которая ещё дополнительно зависит от габаритов проектируемого датчика. Зависимости периода и круговой частоты колебаний от длины маятника представлены на рис.2.
Рисунок 2. – Зависимости собственной круговой частоты колебаний k и периода колебаний T маятника датчика от его длины l.
Для определения длины подвеса датчика l решим задачу поиска наиболее рациональных параметров маятникового датчика, удовлетворяющим следующим требованиям:
- минимальные габариты датчика (l→min);
- как можно большая добротность системы (Д→max);
- минимальные значения коэффициента динамичности(λ→min);
- частота собственных колебаний как можно больше (k→max).
Естественно, удовлетворить все условия невозможно, поэтому сначала определим области существования наиболее близких к оптимальным параметрам значений добротности, построив её зависимости от коэффициента затухания и длины подвеса, от которого непосредственно зависит круговая частота собственных колебаний.
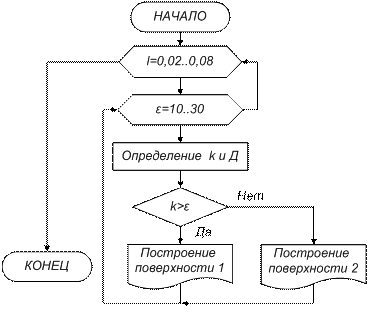
Зависимости добротности представим в виде поверхностей, построение которых реализовано по ниже представленному алгоритму, реализованному в MS EXCEL (рис. 3). Необходимость реализации алгоритма обусловлена различным решением дифференциального уравнения (5) движения маятника при различных значениях коэффициента затухания колебаний и круговой частоты колебаний (7).
Рисунок 3 – Блок-схема реализации алгоритма построения выборочной части поверхности в EXCEL для различных решений.
На рис.4 представлена поверхность зависимости добротности Д от k и ε, удовлетворяющих решению третьего уравнения в выражении (7), максимальное значение добротности для этого случая составляет Д=0,495 при длине маятника l=0,025 м.
Рисунок 4 – Зависимость добротности Д от k и ε при ε >k.
Рисунок 5 – Зависимость добротности Д от k и ε при ε <k.
На рис.5 представлена поверхность зависимость добротности Д от k и ε при ε<k, из которой видно, что наибольшие значения добротности изменяются от 0,502 до 1,107, что более удовлетворяет предъявляемым выше требованиям (по сравнению с результатами, представленными на рис. 4). Определение наиболее рациональных параметров датчика маятникового типа далее будем искать в последней области зависимости Д (рис. 5). При этом следует учитывать, что нужно стремиться, чтобы коэффициент затухания ε был наибольшим.
Отметим также, что значения безразмерного коэффициента затухания d=2ε/k изменяются от 0,903 до 1,999 при соответствующих значениях добротности Д=0,502…1,107. Определим коэффициент динамичности при инерционном возбуждении, который определится по выражению
Как видно из графиков изменения коэффициента динамичности при инерционном возбуждении (рис. 6), наиболее рациональные параметры маятника (k и ε) должны соответствовать безразмерному коэффициенту динамичности d=1,2..2, эти значения приведены в таблице 1.
Рисунок 6 – Зависимость коэффициента динамичности при инерционном возбуждении от коэффициента расстойки z.
Таблица 1 – Значения безразмерного коэффициента динамичности, удовлетворяющие диапазону рациональных параметров маятникового датчика.
|
l\ε |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
| 0,02 |
- |
- |
- |
- |
1,264 |
1,355 |
1,445 |
1,535 |
1,625 |
1,716 |
1,806 |
| 0,025 |
- |
- |
1,212 |
1,313 |
1,413 |
1,514 |
1,615 |
1,716 |
1,817 |
1,918 |
- |
| 0,03 |
- |
1,217 |
1,327 |
1,438 |
1,548 |
1,659 |
1,77 |
1,88 |
1,991 |
- |
- |
| 0,035 |
- |
1,314 |
1,434 |
1,553 |
1,672 |
1,792 |
1,911 |
- |
- |
- |
- |
| 0,04 |
1,277 |
1,405 |
1,533 |
1,66 |
1,788 |
1,916 |
- |
- |
- |
- |
- |
| 0,045 |
1,355 |
1,49 |
1,625 |
1,761 |
1,896 |
- |
- |
- |
- |
- |
- |
| 0,05 |
1,428 |
1,571 |
1,713 |
1,856 |
1,999 |
- |
- |
- |
- |
- |
- |
| 0,055 |
1,498 |
1,647 |
1,797 |
1,947 |
- |
- |
- |
- |
- |
- |
- |
| 0,06 |
1,564 |
1,721 |
1,877 |
- |
- |
- |
- |
- |
- |
- |
- |
Из таблицы 1 видно, что при различных значениях длин маятника варьированием коэффициента затухания, можно достичь нужных значений безразмерного коэффициента затухания, соответствующих максимальным значениям добротности Д.
Для рассматриваемого датчика положения маятникового типа при принятой длине подвеса l=0,04 м собственная круговая частота колебаний
период свободных колебаний .
Период колебаний маятника датчика с учётом вязкого сопротивления в демфпирующей жидкости, определённый опытным путём составляет TD=0,205 с, тогда коэффициент затухания колебаний
Так как ε<k, то имеем случай затухающих колебаний, и согласно выражению (14) имеем
Общее аналитическое решение уравнения (5) после соответствующих преобразований примет вид
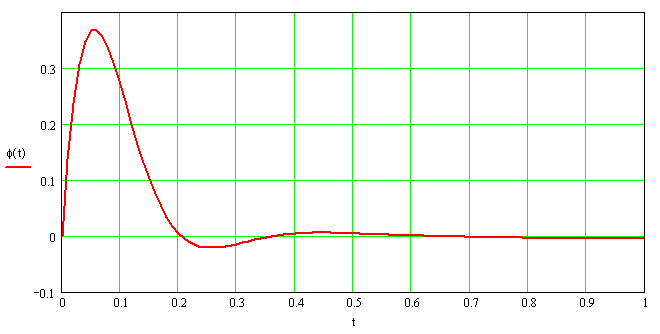
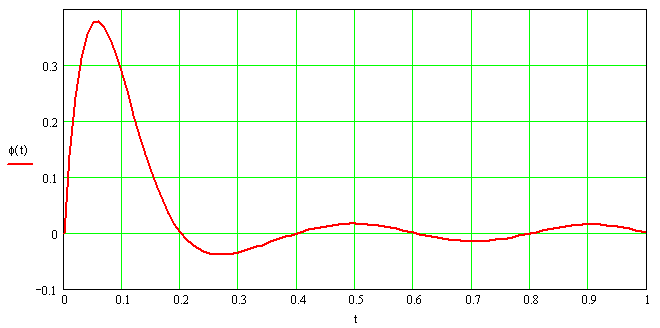
На рис. 7 и 8 представлены графики колебаний маятника датчика при инерционном возбуждении, реализованные в Mathcad.
Рисунок 7 – Колебания маятника датчика при инерционном возбуждении частотой р=5 с-1.
Рисунок 8 – Колебания маятника датчика при инерционном возбуждении резонансной частотой р=k=15,66 с-1.
Как видно из графиков колебаний маятника датчика (рис.7, 8) колебательный процесс апериодический, демпфирование колебаний происходит за 0,2..0,3 с., что меньше времени реагирования оператора, а следовательно, создание автоматизированной системы выравнивания груза на базе мехатронных приводов однозначно будет эффективно.
Список литературы
- Заявка на выдачу патента на изобретение №2010147679/11 от 21.12.2011 г. Авторы: Несмиянов И.А., Токарев В.И.
- Ильин М.М., Колесников К.С., Саратов Ю.С. Теория колебаний: Учеб.для вузов/ Под общ.ред. К.С.Колесникова. – 2-е изд., стереотип. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2003. – 272 с., ил.: (Сер. Механика в техническом университете; Т.4).