Комаров С. Г., независимый исследователь, электромеханик
Известно множество недействующих конструкций «вечных двигателей», в том числе, с использованием свойств магнитного поля. Автор статьи предлагает любознательным старшеклассникам и опытным исследователям вариант «вечного двигателя» с целью детальнее разобраться в интересном магнитном эффекте, вызываемом неоднородным магнитным полем, а также объяснить себе «ошибочность» некоторых утверждений автора в описании конструкции «вечного двигателя», в том числе, возможно, по результатам собственных экспериментальных определений.
Под выражением « вечное движение – вечный двигатель» естественно подразумевать непрекращающееся движение материального тела без совершения или даже с совершением работы. Общеизвестно, что такого механизма ещё никто построить не смог, хотя попытки изобрести его делались уже давно (которые не прекращаются и в наше время).
Однако непреложно доказано: нельзя создать такой механизм, который вечно двигался бы сам собой. И совершенно безнадёжно трудиться над такой задачей. В каждом таком случае упускается из виду какое-нибудь обстоятельство, которое и нарушает работоспособность построенного механизма.
В то же время, как известно, все крупнейшие научные открытия были сделаны часто в результате случайных наблюдений и даже в ходе нелепых экспериментов, которые нередко производились ради развлечения и удовольствия самих экспериментаторов, поставивших перед собой цель проверить опытным путём назревшие предположения с привлечением лежащих на поверхности фактов и теоретических представлений.
Задача автора статьи состоит в том, чтобы возбудить интерес читателя к отысканию и объяснению обстоятельств, приводящих к неработоспособности предложенного «вечного двигателя», показать полезную информацию о веществах, способных намагничиваться, и называемых магнетиками; об однородном намагничивании магнетика и образовании его элементарными токами соответствующего им поверхностного тока (т. е. появлении на поверхности цельного протяжённого или тороидального магнетика дополнительных ампер-витков, которые добавляются к ампер-виткам намагничивающей катушки), определении указанного поверхностного тока значением намагничения, равного по значению линейной плотности поверхностного тока; об определении напряжённости магнитного поля внутри безграничного магнетика – в тороиде с круговой щелью и внутри замкнутой тороидальной катушки; о преломлении линий индукции первоначально однородного магнитного поля, вступающих в среду с большей магнитной проницаемостью – магнетик (в магнетике линии индукции удаляются от нормали, а следовательно, сгущаются); о складывании в каждой точке над магнетиком его магнитного поля с первоначально однородным магнитным полем по правилу параллелограмма, от чего возникает результирующее поле и может возникать результирующая сила; об определении э. д. с. электромагнитной индукции в катушке, пропорциональной быстроте изменения магнитного потока.
Идея создания «вечного двигателя» требует также необходимости привести некоторые экспериментальные и теоретические обоснования такой якобы возможности, одновременно с представлением конструктивных особенностей данного устройства.
Экспериментально установлено, что если магнитный диполь (например, стержневой магнит цилиндрической формы) поместить в однородное магнитное поле (между полюсами другого – внешнего магнита), то этот диполь будет сам по себе ориентироваться вдоль по полю внешнего магнита, но не будет двигаться вдоль линий однородного магнитного поля, поскольку сила притяжения, действующая на северный полюс диполя, будет уравновешена силой, действующей на южный его полюс (см. также, например, книгу Кл. Э. Суорц «Необыкновенная физика обыкновенных явлений», т. 2, Москва «Наука», 1987, стр. 247 – 248, 333 – 334).
На обозначенных страницах этой книги говорится и о том, что если особая форма полюсных наконечников внешнего магнита обеспечивает получение сильно неоднородного магнитного поля, то на магнитный диполь, находящийся в этом неоднородном магнитном поле, будет действовать смещающая сила вдоль направления линий поля. (Но в этой книге нет примера определения напряжённости магнитного поля в круговой щели тороидального магнетика.).
Посчитаем, что аналогичный эффект будет проявляться и в том случае, если сам магнитный диполь пулеобразной формы (т. е. в виде протяжённого цилиндрического бруска с заострённым конусом на одном конце этого бруска) является источником неоднородного магнитного поля, находящимся в первоначально однородном магнитном поле. При этом будем считать пулеобразный магнит не настолько устойчивым, чтобы величина его магнитного поля не зависела от магнитного поля внутри круговой щели тороидального магнетика или внутри тороидальной катушки.
Пусть, например, на «острие» магнитного диполя пулеобразной формы находится северный магнитный полюс, а на цилиндрическом основании этого диполя – южный магнитный полюс. Поместим диполь в магнитное поле внешнего магнита или тороидальной катушки, которое до внесения в него диполя было однородным, и таким образом, чтобы линии индукции, например тороидальной катушки, «вливались» через определённую площадь кругового торца и часть наружной поверхности в южный полюс диполя, обеспечивая силу притяжения между северным полюсом магнитного поля катушки и южным полюсом диполя.
В таком случае будем считать, что при внесении пулеобразного магнита в магнитное поле, которое до этого было однородным, а магнитная проницаемость этого магнита значительно больше, чем в воздушной или же вакуумной среде – в щели тороида или внутри тороидальной катушки, происходит дополнительное сгущение линий индукции внутри магнита – магнит дополнительно намагничивается, образуя более сильное магнитное поле внутри магнита и, в том числе, на остром его конце. Внешнее поле магнита будет складываться в каждой точке над ним с первоначально однородным магнитным полем по правилу параллелограмма, линии индукции стягиваются к магниту, испытывают на его поверхности преломление и располагаются внутри магнита гораздо гуще. От чего возникает результирующее поле и результирующая сила, приводящая диполь в движение.
Обозначенное объяснение лучше к тому же проверить расширенной практикой, поскольку в печатных публикациях нет сведений о практическом применении такого устройства. Но мы поверим в него однозначно, поскольку решаемся в конечном итоге произвести даже нелепые эксперименты (хотя бы в теоретическом плане).
Возможно, например, изготовить тороид из неэлектропроводного магнетика без гистерезиса, для которого прямая и обратная ветви кривой намагничивания совпадают, – феррита, практически почти полностью теряющего свою намагниченность после снятия намагничивающего поля (в примере, отключения тока в намагничивающей обмотке – катушке, намотанной, например, по всей длине тороида), для которого характерно весьма высокое электрическое сопротивление, а направления индукции В и напряжённости Н магнитного поля совпадают (изотропный магнетик).
(Поясним: напряжённость магнитного поля Н пропорциональна количеству магнитных силовых линий в единице сечения – чем больше плотность магнитных линий, тем больше напряжённость магнитного поля. Одинаковая по величине напряжённость магнитного поля Н вызывает в разных материалах различную по величине магнитную индукцию В. Отношение В / Н называется магнитной проницаемостью материала μ, которая равна произведению магнитной проницаемости вакуума (4π · 10-7 гн / м) и относительной магнитной проницаемости материала, например, феррита (порядка нескольких тысяч). В абсолютной системе единиц магнитная индукция В выражается в гауссах, а напряжённость Н магнитного поля в эрстэдах. В СИ магнитная индукция В выражается в тесла, а напряжённость Н в амперах на метр – а / м. 1 тесла равен 104 гс).
Изобразим на рис. 1 такой тороид из магнетика (безграничный магнетик) с узкой круговой щелью внутри его.
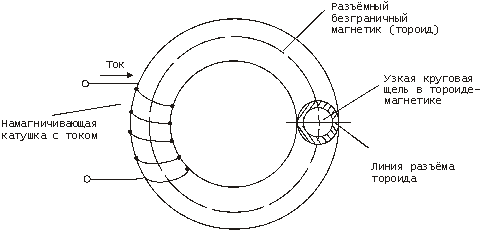
Рис. 1
Тороидальный магнетик состоит из двух частей, т. е. как бы тороид разрезан в своей плоскости (на рис. 1 показана линия разъёма – разреза тороида в сечении), и поверх тороида намотана катушка для подачи в неё постоянного тока.
Если магнетик не намагничен (тока в катушке нет), то в нём нет и кругового магнитного поля. Это значит, что элементарные (молекулярные) токи расположены в нём беспорядочно, так что суммарное их действие равно нулю. При намагничивании магнетика (постоянным током в катушке, намотанной по всей длине тороида) расположение элементарных токов в магнетике становится частично или полностью упорядоченным. Поэтому намагниченный магнетик можно представить как систему мельчайших ориентированных токов.
Действие всех молекулярных токов, например, в примере цельного (сплошного – без круговой щели) тороида было бы такое же, как действие некоторого поверхностного тока, обтекающего намагниченный магнетик, т. е. на поверхности тороида появились бы дополнительные невидимые ампер-витки, которые добавляются к ампер-виткам намагничивающей катушки с током. Но чему равна напряжённость магнитного поля внутри щели тороидального магнетика?
Намагничевание снаружи магнетика и внутри – в узкой щели магнетика показано на рис. 2.
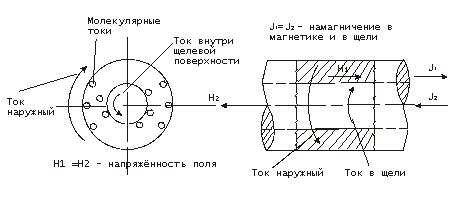
Рис. 2
Магнитное поле можно представить заполненным магнитными линиями, выходящими из северного полюса магнита и входящими в южный полюс. В тороидальном ферромагнитном сердечнике магнитные линии параллельны между собой и замкнуты на себя. Чем больше плотность магнитных линий, тем больше напряжённость магнитного поля. Напряжённость магнитного поля пропорциональна количеству магнитных линий, т. е. магнитной индукции В, которая, как было показано выше, равна произведению магнитной проницаемости материала магнетика и напряжённости магнитного поля Н. Напряжённость Н магнитного поля аналогична механической силе. Она является векторной величиной, т. е. имеет величину и направление.
Напряжённость Н поля внутри щели, параллельной намагничению J, складывается из трёх частей: поля Н0, создаваемого витками намагничивающей катушки, поля Н1 токов на внешней поверхности магнетика и поля Н2 токов на внутренней поверхности магнетика (щели). Т. к. линейная плотность поверхностных токов равна значению вектора намагничения J, то Н1 = Н2 = 4πJ. При однородном намагничивании значение намагничения даёт непосредственно линейную плотность поверхностного тока магнетика, т. е. силу тока на 1 см длины тороида по его средней линии. Поэтому напряжённость Н поля возможно определить по формуле: Н = 4πwi. Здесь w – число витков намагничивающей катушки на единицу длины 1 см, а сила тока i должна измеряться в электромагнитных единицах, при этом Н получается также в электромагнитных единицах (в эрстедах). Если i измерено в амперах, то Н = 0,4πwi эрстед. 1 эрстэд равен 79,58 а / м.
Таким образом, поле в намагничивающей катушке зависит от произведения из силы тока и числа витков на 1 см длины намагничивающей катушки. Это произведение в электротехнике называют числом ампер-витков на сантиметр (а-в / см).
Но токи на внутренней поверхности магнетика (в щели), как показано на рис. 2, имеют противоположное направление, чем токи на внешней его поверхности, поэтому создаваемое ими поле есть Н2 = – 4πJ. (Поле Н1 имеет это же значение, но с положительным знаком). Полная напряжённость поля в щели Н = Н0 + 4πJ – 4πJ = Н0. Т.е. напряжённость магнитного поля внутри безграничного магнетика (в щели) равна напряжённости магнитного поля намагничивающей катушки. При этом катушка, будем считать, намотана по всей поверхности тороида (на рис. 1 катушка намотана на части длины тороида).
Вектор намагничения является основной величиной, характеризующей магнитное состояние вещества – магнетика. При однородном намагничивании магнетика противоположные направления молекулярных токов взаимно компенсируются и остаются только отрезки токов, примыкающие к наружной поверхности магнетика. Поэтому и действие всех молекулярных токов будет такое же, как действие некоторого поверхностного тока, обтекающего намагниченный магнетик. Но при наличии круговой щели в тороидальном магнетике это не так.
Из сказанного выше вытекает метод измерения напряжённости магнитного поля внутри – в щели магнетика. Для этого нужно бы удалить катушку над магнетиком (или, например, создать аналогичную по параметрам катушку) и измерить напряжённость поля, создаваемого катушкой (без магнетика), или же рассчитать напряжённость поля катушки с использованием приведенной выше формулы.
Приведём конкретный пример. Пусть катушка на тороидальном магнетике с круговой щелью имеет 20 витков провода на 1 см длины тороида. w = 20 витков. L = 1 см = 0,01 м. И за счёт напряжения источника тока в катушке обеспечивается ток i = 0,25 а. Тогда с использованием формулы iw = HL находим Н – напряжённость поля. 0,25 · 20 = Н · 0,01. Н = 500 а / м = 5 а / см.
Определим напряжённость Н магнитного поля катушки также по ранее приведенной формуле Н = 0,4πwi. Н = 0,4 · 3,14 · 20 · 0,25 = 6,28 (эрстед). Поскольку 1 эрстед равен 79,6 а / м, то напряжённость Н = 500 а / м = 5 а / см.
Определим магнитную индукцию в катушке в абсолютной системе единиц (якобы без сердечника, поскольку, как определено, напряжённость поля внутри круговой щели тороидального магнетика равна напряжённости поля катушки) В1 = 0,4 πН = 0,4 · 3,14 · 5 а /см = 6,25 гс. Т. к. 1 тесла (тл) равен 10 000 гаусс (гс), то 6,25 гс = 0,000625 тл. А вот если бы тороидальный магнетик в катушке был цельным (без круговой щели), чего нет на самом деле, а относительная магнитная проницаемость его, например, равна 2400, то индукция В2 в тороидальном магнетике определялась бы в значении В2 = 2400 · 6,25 гс = 15 000 гс = 1,5 тл. В системе СИ В2 = 4π · 10-7 гн / м · 2400 · 500 а /м = 1,5 тл.
Измерение напряжённости магнитного поля, например, керамического магнита обычно производят с применением флюксметра, состоящего из витка проволоки, ориентированного перпендикулярно к магнитному полю и соединённого с баллистическим гальванометром.
Изготовим также стеклянный тороид, который изображён на рис. 3.
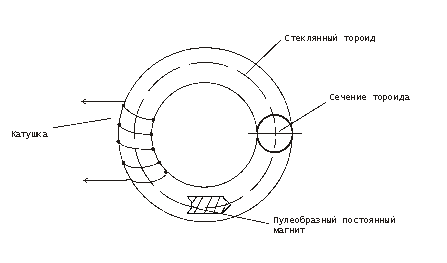
Рис. 3
При этом поместим внутрь стеклянного тороида пулеобразный магнит и откачаем из этого тороида воздух (для уменьшения сопротивления движению пулеобразного магнита). Радиус тороида (на рис. 3 не показан) – до средней линии тороида значительно больше радиуса сечения тороида.
Сначала намотаем поверх стеклянного тороида катушку из тонкого провода по всей его длине (на рис. 3 показаны лишь несколько витков катушки) и подадим в катушку постоянный ток. Магнитное поле катушки через стекло проникает внутрь стеклянного тороида. Посчитаем, что получится ожидаемый результат: постоянный магнит приходит в движение до тех пор, пока подаётся постоянный ток в катушку. В том числе, очевидно, что с переменой направления постоянного тока в катушке изменяется направление движения постоянного магнита.
Затем смотаем со стеклянного тороида большую часть витков катушки и оставим только несколько её витков на длине этого тороида – порядка половины длины пулеобразного магнита, поместим стеклянный тороид в разъёмный безграничный магнетик (тороид), изображённый на рис. 1, и намотаем по всей длине этого тороидального магнетика катушку. Несколько витков провода на длине стеклянного тороида необходимы для того, чтобы по измерению импульсного напряжения и частоте его появления на этих витках констатировать наличие движения пулеобразного магнита. Продолжим рассуждения.
Подадим в катушку на тороидальном магнетике постоянный ток, который обеспечивал бы в круговой щели тороидального магнетика однородное магнитное поле, если бы в ней не было пулеобразного магнита с неоднородным магнитным полем. При наличии в щели магнетика пулеобразного магнита линии индукции, созданные катушкой с током, взаимодействуя с неоднородным магнитным полем пулеобразного магнита, образуют, считаем, круговое движение магнита в щели магнетика, поскольку внешнее поле магнита будет складываться в каждой точке над ним с первоначально однородным магнитным полем по правилу параллелограмма, линии индукции стягиваются к магниту, испытывают на его поверхности преломление и располагаются внутри магнита гораздо гуще. От чего и возникает результирующее поле и результирующая сила, приводящая диполь в движение.
Обычно считается (что связано с понятием принципа работы силового трансформатора), что для образования в замкнутом тороидальном магнетике кругового магнитного поля не обязательно наматывать катушку по всей длине тороида (как и показано на рис.1), т. е. краевые эффекты при ограниченной длине катушки отсутствуют, и напряжённость поля внутри – в щели магнетика целиком определяется напряжённостью поля намагничивающей катушки.
Если это так (а это именно так), то катушку с током возможно заменить наложенным на тороидальный магнетик постоянным магнитом, поляризующим тороидальный магнетик с кольцевой щелью внутри. А это уже путь к созданию «вечного двигателя», поскольку нет потребности в дополнительной энергии на образование однородного магнитного поля в щели тороидального магнетика, т. е. с применением катушки с током. (Износ движущегося магнита от трения о стеклянный тороид и торможение магнита не учитываем. Не учитываем и тормозящее действие индукционного тока, поскольку отмеченные торможения компенсируются действием энергии поляризации тороидального магнетика. Что не мешает называть движение пулеобразного магнита «вечным движением»).
Пулеобразный магнит, пролетая через вспомогательную катушку, расположенную на стеклянном тороиде, индуцирует в этой катушке импульс тока, при этом индукционный ток в катушке зависит от скорости пулеобразного магнита относительно катушки. Таким образом рассматриваемое устройство одновременно является и генератором электрических импульсов.
Казалось бы представленное обозрение конструкции «вечного двигателя» имеет мало общего с реальностью, но в значении познавательного характера оно, кроме того, учит аналитическому мышлению и способствует развитию творческих способностей начинающих исследователей.
Источники информации:
1. Кл. Э. Суорц «Необыкновенная физика обыкновенных явлений», т. 2, Москва «Наука», 1987, стр. 247 – 248, 333 – 334.
2. И. В. Савельев «Курс общей физики» 2, Москва, «Наука», 1966, стр. 109 – 110, 113 – 120.


