Введение. Долговечность является важным показателем надежности клиноременной передачи и привода механического пресса в целом. Надежность ременной передачи во многом определяет работоспособность пресса, время эксплуатации до отказа, длительность межремонтного цикла и стоимость эксплуатации. Расчет срока службы передачи необходим для организации ремонтной службы и определения направления повышения надежности привода.
Анализ предшествующих исследований. Долговечность ременной передачи определяется ресурсом работы передачи до момента отказа всей передачи или нескольких ремней.
Клиноременная передача в целом относится к ремонтируемым (восстанавливаемым) изделиям [1, с. 8]. Отказ одного из элементов (ремней) как правило, не приводит к отказу всей системы, наступает частичный отказ, когда система сохраняет работоспособность. Передача эксплуатируется в циклически нерегулярном режиме до предельного состояния или полного отказа нескольких элементов, после чего теряет работоспособность. Нормируемым показателем надежности передачи является вероятность безотказной работы при заданной наработке на отказ Pп(t) и средний ресурс работы Tп. Ремни относятся к неремонтируемым (не восстанавливаемым) элементам, отказ которых приводит к полной потере работоспособности. Показателями надежности ремней являются средний ресурс работы (наработка на отказ) Tср, вероятность безотказной работы в течение заданного периода Pр(t) и плотность распределения вероятности отказов fр(t) [2, с. 89]. Для отдельного ремня все параметры взаимосвязаны зависимостями [2, с. 97]:
– вероятность безотказной работы, т. е. безусловная вероятность того, что на интервале времени от 0 до t не наступит отказ (функция надежности)
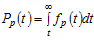 ;
;
– наработка на отказ
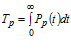 ;
;
– опасность отказа
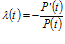 .
.
Опасность отказа λ(t) есть локальная характеристика надежности, представляющая собой вероятность того, что элемент откажет после некоторого периода t.
Плотность распределения вероятности отказов fр(t) определяется принятым законом надежности.
На практике большое распространение получил экспоненциальный закон надежности, согласно которому 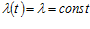 и тогда
и тогда
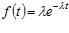 .
.
Несложно получить, что функция надежности
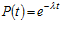 .
.
Экспоненциальный закон надежности обеспечивает простое решение многих задач в теории надежности, но такой закон надежности хорошо описывает только внезапные отказы. Отказы, возникающие в результате износа и старения элементов, не подчиняются экспоненциальному закону, т. к. их надежность со временем изменяется. Такие отказы, называемые постепенными, хорошо описываются другими законами, среди которых наибольшее распространение получил двухпараметрический закон распределения Вейбулла [2, с. 102]
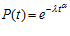 .
.
Основным достоинством этого закона является дополнительный параметр α, отражающий интенсивность старения элемента, при условии, что опасность отказа λ является постоянной величиной.
Таким образом, для определения долговечности ремней необходимо знать значение параметров λ и α. Надежность передачи в целом Pп(t) определяется надежностью отдельных ее элементов.
Цель работы. В статье представлена методика расчета долговечности клиноременной передачи механических прессов с учетом специфических условий их эксплуатации.
Материал и результаты исследований. Клиноременная передача пресса является в целом системой с n независимыми элементами (ремнями). В такой системе отказ элементов (ремней) происходит независимо друг от друга. Отказ всей системы наступает тогда, когда происходит отказ одного или нескольких элементов. В первом случае отказ системы происходит при отказе любого одного элемента. Считается, что в такой системе элементы соединены последовательно в смысле надежности [2, с. 133]. Во втором случае отказ системы наступает тогда, когда отказывают несколько r элементов (r < n). До момента отказа r-го ремня передача сохраняет свою номинальную работоспособность. При отказе одного из элементов ременная передача сохраняет работоспособность, однако ее тяговая способность снижается, увеличивается нагрузка на остальные ремни, возрастает потеря скорости и энергетическая надежность привода в целом снижается. Такая передача считается передачей с параллельным соединением элементов.
Если система состоит из n элементов с надежностью каждого из них p1(t), p2(t), …, pn(t), то надежность работы всей передачи будет
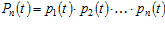 .
.
Выражая функцию надежности через опасность отказов, находим
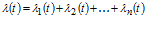 .
.
Если средний ресурс работы одного ремня Ti, тогда среднее время работы передачи до первого отказа составляет
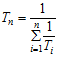 .
.
В частном случае, когда все ремни имеют одинаковую надежность, т. е. 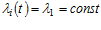 , то при экспоненциальном законе надежность и опасность отказов всей передачи составляют
, то при экспоненциальном законе надежность и опасность отказов всей передачи составляют 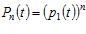 ,
, 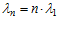 .
.
Среднее время работы всей передачи до первого отказа составляет
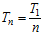 . (1)
. (1)
Здесь λ1 и Т1 обозначают опасность отказов и ресурс работы одного ремня, а λп и Тп – опасность отказов и ресурс работы всей передачи.
Во втором случае, когда отказ передачи происходит после отказа k-го ремня, нагрузка оставшихся ремней увеличивается и их надежность уменьшается. При отказе r-го ремня передача теряет свою работоспособность и наступает полный отказ системы. В теории надежности такой поток отказов рассматривается как процесс типа гибель [2, с. 297].
На интервале времени между двумя отказами надежность передачи постоянна и определяется только количеством оставшихся ремней, и к моменту наступления очередного отказа опасность отказа оставшихся k ремней составляет 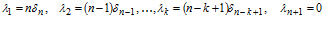 , где δi – опасность отказа оставшихся k ремней.
, где δi – опасность отказа оставшихся k ремней.
Если надежность всех ремней близка к единице, то приближенно надежность всей передачи составляет 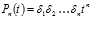 , а ресурс работы передачи составляет
, а ресурс работы передачи составляет
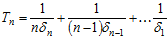 .
.
В частном случае, когда надежность отдельных ремней не зависит от количества отказов других ремней, имеем
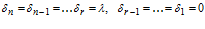
Тогда 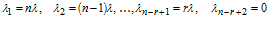 .
.
Средний ресурс всей передачи до момента отказа r-го ремня равен
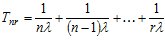 , (2)
, (2)
или при n и r больше 5÷8
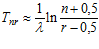 . (3)
. (3)
Если предположить, что отказ передачи происходит при отказе всех элементов (n = r), то при экспоненциальном законе надежности
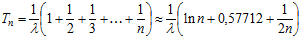 . (4)
. (4)
Т. о. надежность всей передачи определяется надежностью отдельных ремней и условием наступления отказа передачи.
В технической литературе ввиду отсутствия достоверных данных о значениях параметров функции надежности λ и α средний ресурс безотказной работы отдельных ремней рекомендуется определять по эмпирической зависимости [3, с. 62; 4, с. 89]
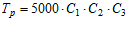 , (5)
, (5)
где С1 – коэффициент, учитывающий режим работы передачи;
С2 – коэффициент, учитывающий значение передаваемой мощности;
С3 – коэффициент, учитывающий относительную скорость ремня.
Номинальное значение среднего ресурса работы Тр отдельного ремня по (5) равное 5000 часов, является скорее желательным, чем реальным значением. Применительно к клиноременным передачам механических прессов дополнительно учитывается неравномерность нагружения передачи в течение одного технологического цикла. В работе [4, с. 98] приведены рекомендации по уточнению коэффициента режима работы С1, учитывающие влияние формы цикла нагружения которые, однако, существенно не уточняют итоговый результат.
Практика эксплуатации клиноременных передач механических прессов и опытные данные показывают, что действительные значения среднего ресурса работы ремней значительно меньше величины, определяемой по указанной зависимости, поэтому она не может быть рекомендована для использования.
Надежность безотказной работы отдельных ремней в общем случае в результате старения и износа постепенно снижается и определяется законом Вейбулла. При известных параметрах λ и α среднее время работы ремня до момента отказа составляет [2, с. 102]
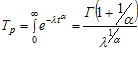 , (6)
, (6)
где Г(z) – гамма-функция, определяемая как
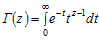 .
.
При экспоненциальном законе надежности ремней ресурс работы одного ремня определяется как величина, обратно пропорциональная значению λ
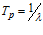 . (7)
. (7)
Для ориентировочных расчетов значения параметров надежности клиновых ремней передач механических прессов определены на основе производственных испытаний. Параметр α, учитывающий старение ремней рекомендуется принимать α = 1,015…1,05. Большие значения принимаются для прессов с меньшим номинальным усилием и большим передаточным отношением клиноременной передачи. Параметр λ, определяющий опасность отказа для клиноременных передач листоштамповочных прессов следует принимать не менее 3*10-4, для передач КГШП – не менее 3,7*10-4.
Наиболее достоверные значения среднего ресурса работы ремней определяются по условиям усталостной прочности. Усталостная прочность ремней определяется частотой нагружения ремней, значениями максимальных напряжений в ветвях ремней и формой цикла нагружения [5–7].
Частота нагружения определяется величиной частоты пробегов ремня в единицу времени. В общем случае эффективная частота пробегов
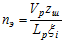 , (8)
, (8)
где Vp– линейная скорость ремня
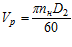 ;
;
nн – номинальное число оборотов ведомого шкива (маховика);
D2 – расчетный диаметр ведомого шкива (маховика);
zш– число шкивов;
Lр – расчетная длина ремня;
ξi – коэффициент, учитывающий снижение напряжения изгиба на малом шкиве, т. е. форму цикла нагружения. При передаточном отношении передачи больше 3÷4 коэффициент ξi равен примерно числу шкивов (2).
Максимальное напряжение в ведущей ветви передачи на дуге покоя малого шкива определяется как сумма отдельных напряжений
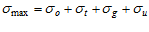 , (9)
, (9)
где σо –напряжение начального натяжения;
σt – напряжение от нагрузки
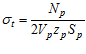 ;
;
Np – передаваемая мощность;
zp – число ремней в передаче;
Sp – номинальная площадь сечения ремня;
σо – напряжение от центробежных сил
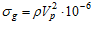 , МПа;
, МПа;
ρ – эквивалентная плотность ремней ρ = 1230…1300 кг/м3;
σо – напряжение изгиба на малом шкиве
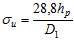 ; (10)
; (10)
hp – номинальная высота сечения ремня;
D1 – расчетный диаметр малого шкива.
Число циклов нагружения до разрушения по принятой теории разрушения ремней [7, с. 114]
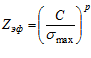 , (11)
, (11)
где С, р – показатели кривой выносливости.
В работе [6, с. 19] для клиновых ремней при предполагаемом числе циклов Zэф < 107 рекомендуется принимать С = 90…100, а показатель р = 7…11. При Zэф = 107…109 рекомендуется принимать С = 30, р = 11, наконец, при Zэф > 109 рекомендуется принимать С = 38,2, а показатель р = 11. Такой разброс значений совершенно не имеет логического объяснения, поэтому наиболее близкими к действительным являются значения параметров, рекомендованные в работе [7, с. 114], а именно С = 30, р = 11 при любом числе циклов нагружения.
Для клиноременных передач механических прессов необходимо учитывать неравномерность нагружения передачи на протяжении относительно длительного периода времени, большем на порядок чем время технологического цикла. Если принять, что в течение длительного времени (например одной смены) пресс работает только часть времени с номинальной нагрузкой, а оставшуюся часть времени с нагрузкой меньше номинальной (предварительные переходы штамповки, холостой ход и др.) фактическое число циклов работы ремня до разрушения необходимо увеличить на величину kф. Коэффициент эквивалентной нагрузки kф для листоштамповочных прессов следует принимать 1,13…1,17, для кривошипных горячештамповочных прессов kф принимается равным 1,08…1,12.
При известном числе циклов нагружения средний ресурс работы ремня будет
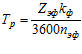 . (12)
. (12)
Пример расчета. Клиноременная передача горизонтально-ковочной машины В-111 состоит из 8 ремней сечения С. Передаваемая мощность Np = 14 кВт, передаточное отношение 9,34. Расчетный диаметр ведущего шкива D1 = 166 мм, диаметр ведомого шкива D2
= 1550 мм. Расчетная длина ремней Lp = 5600 мм. Число оборотов ведомого шкива (маховика) nн = 72 об/мин. Напряжение начального натяжения σ0 = 1 МПа.
Максимальное напряжение в ведущей ветви передачи по (9) σmax = 7,017 МПа. Напряжение изгиба на малом шкиве по (10) σи = 4,07 МПа. Число пробегов ремня по (8) nэ =1,087. Предельное число циклов нагружения по (11) Zэф = 8,728*106. Расчетный ресурс работы одного ремня до отказа по (12) Tp = 2119 ч.
Принимаем параметры закона надежности λ = 3,6*10-4, α = 1,015.
Средний ресурс работы ремня при экспоненциальном законе надежности по (7) Tp = 2778 ч, а при законе надежности Вейбулла по (6) Tp = 2190 ч. Ресурс работы ремня по (5) составляет 6000 ч, что явно не соответствует действительным значениям. Среднее время работы передачи до первого отказа при экспоненциальном законе надежности по (1), или по закону Вейбулла по (2) при r = 7 составляет Tnr = 347 ч. Средний ресурс работы передачи до отказа 2-х ремней (r = 6) по точной формуле (2) Tnr = 744 ч, а по приближенной формуле (3) Tnr = 745,2 ч. Укажем, что среднее время работы передачи до отказа всех ремней при экспоненциальном законе надежности по (4) Tn = 7550 ч.
Приведенные данные показывают, во-первых, достаточно приемлемую точность для оценки долговечности клиноременной передачи. Во-вторых, видно, что закон надежности Вейбулла лучше описывает интенсивность отказов ремня по сравнению с экспоненциальным законом. Наконец, видно, что ресурс работы передачи до первого отказа чрезвычайно низкий. Если увеличить число ремней n до 9 и считать, что отказ передачи произойдет при отказе 7-го ремня (r = 7), ресурс работы увеличивается до 1050 ч.
Выводы.
1. Долговечность клиноременной передачи пресса определяется в первую очередь усталостной прочностью клиновых ремней.
2. Предельное значение числа циклов нагружения ремней до разрушения определяется формой графика нагружения, частотой циклов нагружения и величиной максимальных напряжений в ремнях.
3. Максимальное напряжение в ведущей ветви ремня зависит от геометрических параметров ремней, шкивов, условий эксплуатации.
4. Основное влияние на надежность ремней оказывают начальное натяжение передачи и напряжения изгиба.
Библиографический список
-
Шор Я.Б. Термины и показатели надежности в технике. Основные вопросы надежности и долговечности машин. Учебн. пособие. – М.: МАТИ, 1969. С. 7–21.
-
Гнеденко Б.В., Беляев Ю.К., Соловьев А.Д. Математические методы в теории надежности. – М.: Наука, 1965. –524 с.
-
Карбасов О.Г. Надежность клиноременных передач. – М.: Машиностроение, 1976. – 73 с.
-
Пожидаев Н.Н., Богданов Э.Ф. К расчету клиноременных передач кривошипных прессов на долговечность. Труды МВТУ, № 263. – М.: Машиностроение, 1978. С. 88–100.
-
Буланов Э.А. Расчет ременных передач. Вестник машиностроения. – 2001,– № 12. С. 14–21.
-
Буланов Э.А., Зубарев А.А. Расчет ременных передач на заданный ресурс. Вестник машиностроения. – 1995,– № 1. С. 18–20.
-
Пронин Б.А., Ревков Г.А. Бесступенчатые клиноременные и фрикционные передачи (вариаторы). – М.: Машиностроение, 1980. – 320 с.
