Научный руководитель:
Ахметсафина Римма Закиевна
Доцент кафедры УРПО отделения Программной инженерии Национального исследовательского университета «Высшая школа экономики»
Scientific advisor:
Rimma Akhmetsafina
Associate Professor of Software Engineering Department in School of Software Engineering
National Research University Higher School of Economics
Псевдокаркасная модель (pseudo-wireframe) – 3D-модель, представляющая собой совокупность вершин и ребер (рис. 1). Может включать в себя дополнительные ребра, которые принадлежат проекции, но могут не принадлежать итоговому объекту.
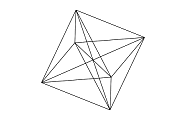
Рис. 1
Каркасная модель (wireframe) – 3D-модель, которая однозначно определяет форму отображаемого многогранного объекта (рис. 2).
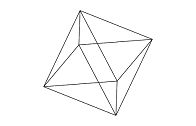
Рис. 2
Solid объект – 3D-объект, представляющий собой совокупность вершин, ребер и граней (рис. 3).
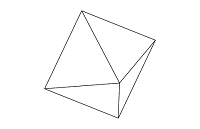
Рис. 3
Комплексный чертеж - это совокупность двух или более (до шести) взаимосвязанных ортогональных проекций геометрической фигуры, расположенных на одной плоскости чертежа (рис. 4).
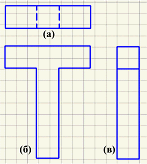
Рис. 4 – (а) – вид сверху (Top View), (б) – вид спереди (Front View), (в) – вид справа (Side View 1).
Модели в методе отображения границ создаются при помощи топологии и геометрических объектов. Основными топологическими единицами являются: faces (лицевые грани, или поверхности), edges (ребра) и vertices (вершины). Face – это ограниченная часть поверхности, относящаяся в некоторому ребру, ребро – сторона грани. В рамках этого подхода также выделяют алгоритмы восстановления псевдокаркасной модели, которая с 1981 г. является одним из шагов в восстановлении solid объектов.
Основной концепцией CSG является возможность математического описания любых сложных объектов при помощи более простых. Простейшими телами в CSG являются примитивы – тела простой формы, такие как куб, сфера, цилиндр, призма. Более сложные объекты создаются при помощи применения булевых операций (объединение, пересечение, разность) к некоторому набору примитивов.1.
На вход программе подаются три проекции, которые представлены наборами вершин и ребер. Все вершины представляются в виде их координат x, y, z и порядковых номеров этих вершин. Пусть
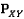 описывает набор вершин в координатной плоскости XY, тогда
описывает набор вершин в координатной плоскости XY, тогда 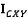 описывает набор вершин, которые соединяются с элементом из
описывает набор вершин, которые соединяются с элементом из 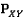 ребрами. Если три или больше вершин находятся на одной прямой, они объединяются в группу.
ребрами. Если три или больше вершин находятся на одной прямой, они объединяются в группу. 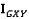 описывает номера групп, к которым принадлежит вершина из
описывает номера групп, к которым принадлежит вершина из  (рис. 5, [1] стр. 22).
(рис. 5, [1] стр. 22).
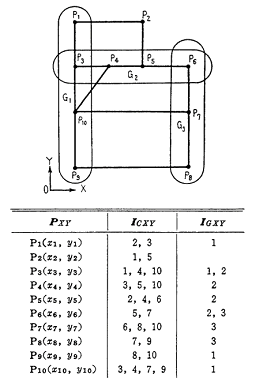
Рис. 5
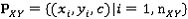
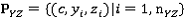 , (1)
, (1)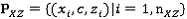
где
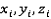 - координаты i-го элемента списка вершин,
- координаты i-го элемента списка вершин,с – некоторая координата,
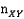 - количество вершин в
- количество вершин в 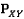 ,
,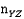 - количество вершин в
- количество вершин в 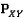 ,
,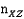 - количество вершин в
- количество вершин в 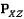 .
.Пусть (
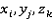 ) представляется комбинацией i, j, k элементов уравнения (1) так, что выполняются условия
) представляется комбинацией i, j, k элементов уравнения (1) так, что выполняются условия 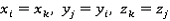 . Тогда (
. Тогда (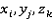 ) образуют элемент матрицы связанных вершин
) образуют элемент матрицы связанных вершин 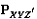 . Эти операции применяются в (1) ко всем комбинациям i, j, k. Условия
. Эти операции применяются в (1) ко всем комбинациям i, j, k. Условия 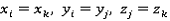 выполняются следующим образом:
выполняются следующим образом:Если
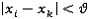 , тогда
, тогда 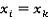
Если
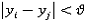 , тогда
, тогда 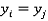 ,
,Если
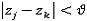 , тогда
, тогда 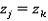
где
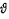 – положительной число, обозначающее погрешность.
– положительной число, обозначающее погрешность.Пусть
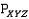 и
и 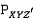 – две разные вершины в
– две разные вершины в 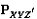 .
. 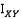 ,
, 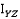 ,
, 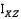 используются для i, j, k в
используются для i, j, k в 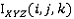 .
. 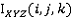 является элементом
является элементом 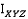 соответствующим
соответствующим 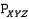 .
.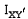 ,
, 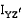 ,
, 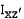 используются для обозначения i, j, k в
используются для обозначения i, j, k в 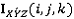 .
. 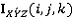 является элементом
является элементом 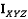 соответствующим
соответствующим 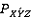 . Далее
. Далее 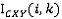 обозначает k-ый элемент
обозначает k-ый элемент 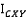 , который является элементом
, который является элементом 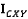 соответствующим
соответствующим 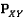 .
. 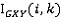 обозначает k-ый элемент
обозначает k-ый элемент 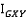 , который является элементом
, который является элементом 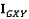 соответствующим
соответствующим 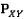 . Похожие переменные принимаются для плоскостей YZ и XZ.
. Похожие переменные принимаются для плоскостей YZ и XZ.Таким образом результатом следующих булевых операций является определение того, соединяются ли вершины
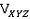 и
и 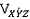 ребром:
ребром: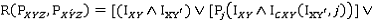
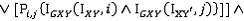
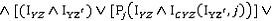
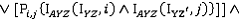
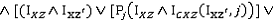
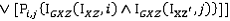 При восстановлении лицевых поверхностей используются следующие правила.
При восстановлении лицевых поверхностей используются следующие правила.a) Существует k лицевых поверхностей, каждая из которых содержит вершину, находящуюся на пересечении k ребер;
b) Ребро представляет собой линию пересечения двух лицевых поверхностей, а в списках ребер лицевых поверхностей вершины этого ребра идут в разном порядке;
c) Граница лицевой поверхности замкнута.
Для начала необходимо используя эти правила найти грань, которая может быть уникально определена. Затем нужно провести поиск всех ребер грани, сохранить эти ребра в список и отсортировать, чтобы они удовлетворяли правилу (b). В конце нужно отсортировать вершины ребер против часовой стрелки для внешней лицевой поверхности и по часовой стрелке для внутренней поверхности грани.
Это был один из первых подходов к восстановлению solid объектов. Впоследствии алгоритмы, в которых происходит работа с ребрами, получили общее название Метод отображения границ.
1.1.1. Алгоритм Markowsky и Wesley
В 1980 году George Markowsky, профессор университета Мэна, и Michael A. Wesley из исследовательского института IBM Томаса Уотсона в своей работе “Fleshing out Projections” [2] предложили использовать псевдокаркасную модель как промежуточную стадию процесса восстановления solid объекта. Эта работа до сих пор является основополагающей для разработки новых алгоритмов в рамках метода отображения границ. Согласно подходу Markowsky и Wesley на вход алгоритму подаются три файла проекции комплексного чертежа (вид сверху, вид спереди и вид справа). Предполагается, что все проекции заданы в одинаковом масштабе. Файл каждой проекции анализируется, и информация о хранящихся в нем геометрических компонентах – вершинах и ребрах – записывается в матрицы 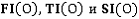 :
:
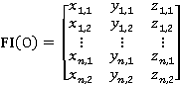 ,
,где 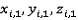 - координаты вершины – начала ребра,
- координаты вершины – начала ребра,
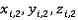 - координаты вершины – конца ребра,
- координаты вершины – конца ребра,
где 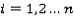 ,
,
n – количество ребер в проекции.
Далее для каждой проекции создаются матрицы 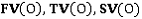 и
и 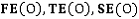 для хранения информации о вершинах и ребрах соответственно:
для хранения информации о вершинах и ребрах соответственно:
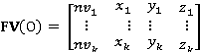 ,
,где 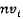 – порядковый номер i-ой вершины,
– порядковый номер i-ой вершины,
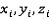 - координаты i-ой вершины, i =1,2,…,k
- координаты i-ой вершины, i =1,2,…,k
k – количество вершин проекции.
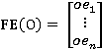 ,
,где 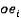 - объект типа «ребро», i = 1,2,…,n
- объект типа «ребро», i = 1,2,…,n
n – количество ребер проекции.
Каждый объект типа «ребро» содержит следующую информацию:
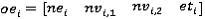 ,
,где 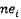 - порядковый номер ребра,
- порядковый номер ребра,
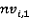 – порядковый номер вершины, определяющей начало ребра,
– порядковый номер вершины, определяющей начало ребра,
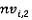 - порядковый номер вершины, определяющей конец ребра,
- порядковый номер вершины, определяющей конец ребра,
 - тип ребра (обычное / невидимое),
- тип ребра (обычное / невидимое),
i = 1,2,…,n,
n – количество ребер проекции.
Проекции могут быть определены в любой части координатной плоскости, поэтому для того чтобы объединить их в одной модели необходимо, чтобы хотя бы одна вершина каждой проекции находилась на оси X, хотя бы одна вершина каждой проекции находилась на оси Y, а сами проекции полностью находились в первом квадранте. После этого необходимо расположить проекции друг относительно друга в 3D пространстве. Для этого боковая проекция поворачивается на 90є вокруг оси Y таким образом, что оказывается на координатной плоскости YZ, а верхняя проекция поворачивается на 90є вокруг оси X таким образом, что оказывается на координатной плоскости XZ (рис. 6).
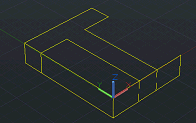
Рис. 6
Далее полученные данные объединяются в одной матрице. На этом этапе каждая проекция находится на своей координатной плоскости. Для каждой проекции из каждой вершины необходимо провести перпендикуляр к соответствующей координатной плоскости: XY для передней проекции, YZ для боковой проекции и XZ для верхней проекции (рис. 7).
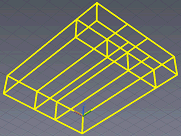
Рис. 7
В полученной модели нужно определить точки пересечения ребер (рис. 8).
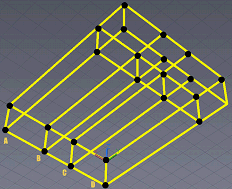
Рис. 8
Для того чтобы найти не ортогональные к проекциям ребра, нужно спроецировать модель на одну из координатных плоскостей. Для каждой вершины в модели ищется вершина на соответствующей проекции и соответствующими двумя координатами (x, y для фронтальной проекции; x, z для верхней проекции; y, z для боковой проекции). В проекции находятся и запоминаются координаты вершин, которые соединены ребрами с проверяемой вершиной. В модели ребрами соединяются вершины с запомненными двухмерными координатами и проверяемая вершина, если таких ребер еще нет в матрице (рис. 9). Эта операция выполняется для каждой вершины модели, и каждая вершина сравнивается с каждой проекцией.
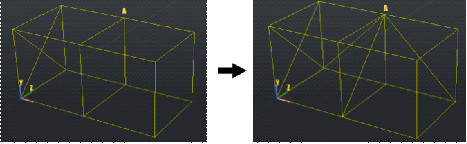
Рис. 9
На этом этапе в модели слишком много лишних ребер. Необходимо спроецировать ее на каждую координатную плоскость и сравнить с соответствующей проекцией. Ребра модели, не принадлежащие проекции, удаляются (рис. 10). Таким образом на выходе получается псевдокаркасная модель, заданная тремя проекциями.
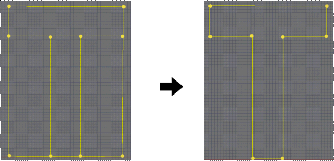
Рис. 10
1.1.2. Алгоритм Sakurai и Gossard
В 1983 году Sakurai и Gossard [3] модифицировали алгоритм Markowsky и Wesley. На вход алгоритму подаются три проекции комплексного чертежа. Модифицированный алгоритм обрабатывает цилиндрические, конические, сферические и тороидальные примитивы, прямолинейные невидимые ребра (hidden edges) и невидимые дуги (hidden arcs), которые не учитывались в алгоритме Markowsky и Wesley.
В инженерных чертежах видимые на проекции ребра, образованные пересечением двух граней, обозначаются сплошными линиями, будем называть их стандартными (standart edge, ES).
Невидимые на проекции ребра и дуги обозначаются пунктирными линиями.
Тела вращения, такие как тор и сфера, не имеют ребер. На проекциях комплексного чертежа изображаются не ребра, а контуры таких тел. Будем называть их силуэтными ребрами (silhouette edge). Различают прямые силуэтные ребра (ELS – line silhouette edge) и силуэтные дуги (EAS – arc silhouette edge).
В объектах с плоскими и изогнутыми лицевыми поверхностями две лицевые поверхности могут соприкасаться вдоль мнимого общего ребра. Будем называть его ребром касания (tangency edge). Ребра касания так же могут быть прямыми (ELT – line tangency edge) и дугами (EAT – arc tangency edge). Ни на одной из проекций ребра касания не видны (рис. 11).
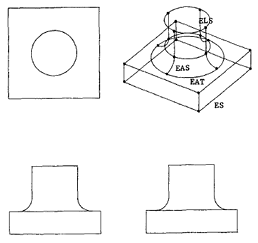
Восстановление вершин на 2D проекциях. Используя подсчет точек пересечения можно найти вершины, образованные только стандартными ребрами. Вершины, образованные силуэтными ребрами, ребрами касания этим способом найти невозможно. Поэтому в каждой проекции необходимо найти вершины, где прямые соприкасаются с дугами (вершины с атрибутом касания), и вершины, где параллельные осям координат прямые соприкасаются с дугами (вершины с атрибутом «силуэт»). После этого используя координаты найденных вершин, линии в остальных проекциях обрезаются, и образуются вершины-кандидаты на силуэтных ребрах и ребрах касания (вершины с атрибутами «создана ребром касания» и «создана силуэтным ребром»). Такие вершины могут иметь более одного атрибута.
Восстановление 3D вершин. 3D координаты создаются из пар двухмерных координат, которые имеют одну общую координату (x, y или z). После этого вершина проецируется на третью проекцию. Если проецируемая вершина совпадает с одной из вершин этой проекции, то 3D вершина найдена. На этом этапе создаются четыре типа вершин:
· Вершина, образованная стандартными ребрами (вершина с параметром «стандартная»);
· Вершина с параметром касания, которая формируется из трех вершин: одной с параметром касания и двух вершин с параметрами «создана ребром касания»;
· Вершина с параметром «силуэт», которая формируется из трех вершин: одной с параметром «силуэт» и двумя вершинами с параметрами «создана силуэтным ребром»;
· Вершина с параметром «двойной силуэт», которая формируется из двух вершин с параметром «силуэт».
После этого восстанавливаются вершины непосредственно из проекций. Тороидальные поверхности выделяются, если на трех проекциях:
· две дуги на различных проекциях имеют одинаковый радиус;
· одна из координат центров двух дуг совпадает;
· расстояния от центральных точек проекций до центра дуги в третьей проекции одинаковы.
Сферические поверхности выделяются, если на трех проекциях:
· 3D вершина, которая формируется из центров дуги на двух проекциях, имеет соответствующий центр дуги в третьей проекции.
Так как тор формируется из дуг, то на его поверхности можно генерировать вершины. Этим вершинам задается параметр «тор».
Ребра формируются из 3D вершин, полученных на втором шаге и могут быть трех типов:
· Стандартные ребра: Для двух 3D вершин проверяется, лежат ли их проекции на одной линии или арке в каждой проекции. Если это условие выполняется, вершины соединяются ребром или аркой.
· Силуэтные ребра: Для двух 3D вершин с параметром «силуэт» проверяется, лежат ли их проекции на одной линии или дуге в каждой проекции. Если это условие выполняется, вершины соединяются ребром или дугой.
· Ребра касания: Линейно касающиеся ребра формируются из двух вершин с параметром касания, чьи 2D вершины лежат на одной дуге или коаксиальной дуге под одним углом (рис. 12).
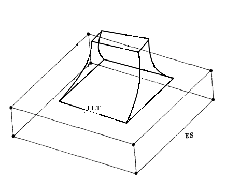
Рис. 12
Дуговое ребро касания (рис. 13, [1] стр. 248) формируются следующим образом. Для двух дуговых ребер, каждое из которых имеет хотя одну вершину с параметром касания, параметром тора или параметром сферы, проверяются, лежат ли они на одном торе или одной сфере. Если это условие выполняется, создается дуговое ребро касания при помощи соединения двух вершин каждого дугового ребра.
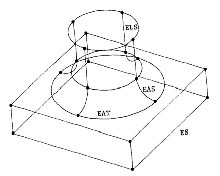
Рис. 13
В 2013 году Lappo Governi, Rocco Furferi, Matteo Palai и Yary Volpe предложили метод восстановления 3D моделей из растровых 2D изображений [4]. Их подход заключается в построении каркасной модели объекта в виде воксельного облака, после чеговычисляются возможные пересечения линий. Сами линии помечаются порядковыми номерами. Далее 3D каркасная модель строится из сплайнов, начинающихся из каждой найденной линии. Линии в зонах пересечения перепроверяются. Они такжепредложили свой метод создания поверхностей в каркасной модели, основанный на работе Balai и Waggenpack [5].
Первые исследования в рамках второго подхода к восстановлению 3D объектов по 2D проекциям были произведены Aldefel в 1983 году [1]. На входе в программу принимаются три проекции, из которых считываются данные о примитивах. Aldefel описывает возможные связи между примитивами. Одной из основных связей является CONTACT(n, m), которая обозначает что n и m связаны хотя бы одной общений точкой. Петлями являются контуры фигуры, например фигура на рисунке 14а является контуром, петлей, фигура на рисунке 14б содержит петлю в петле, а фигура на рисунке 14в является петлей с линией внутри.
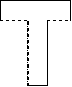
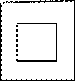

а) б) в)
Шаг 2: Найти, сохранить в списке все элементарные петли (петли, которые не содержат других петель) и отметить их как «открытые».
Шаг 3: Вычисление объема всех «открытых» петель и выбор петли P с максимальным объемом. Также случайным образом выбирается проекция
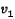 , которая будет считаться базовым силуэтом.
, которая будет считаться базовым силуэтом. Шаг 4: Предположим, что P описывает базовый силуэт одного или нескольких объектов. Для того чтобы доказать или опровергнуть это, необходимо выполнить следующий алгоритм:
· Случайным образом выбирается проекция
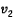 и в ней ищутся все прямоугольные силуэты
и в ней ищутся все прямоугольные силуэты 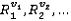 , которые совпадают с P. Если таких силуэтов не найдено, выйти из алгоритма.
, которые совпадают с P. Если таких силуэтов не найдено, выйти из алгоритма. · В оставшейся проекции
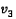 найти для каждого
найти для каждого 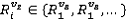 прямоугольный силуэт
прямоугольный силуэт 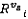 , совпадающий как с
, совпадающий как с 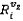 , так и с P. Если таких силуэтов не найдено, выйти из алгоритма.
, так и с P. Если таких силуэтов не найдено, выйти из алгоритма.· Проанализировать P и найти все примитивы, которые требуют наличия линий в одной или обеих проекциях (базовая проекция не учитывается).
· Для каждой пары (
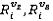 ) найти полный список линий, которые описываются их примитивами. Если операция прошла успешно, итоговый объект представлен объединением
) найти полный список линий, которые описываются их примитивами. Если операция прошла успешно, итоговый объект представлен объединением 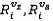 и списка линий, полученных на этом шаге.
и списка линий, полученных на этом шаге.Шаг 5: «Расширить» петлю P, создав все петли, которые включают в себя петли, прилежащие к P, если их еще не существует. Добавить их в список, отметить новые зависимости, отметить новые петли как «открытые», а P пометить как «закрытую».
Шаг 6: Спроецировать полученные объекты на плоскости проекций, чтобы определить, описываются ли они входными проекциями. Если это так, то на этом работа алгоритма завершается, в противном случае перейти к шагу 3.
Описанный алгоритм работает только для объектов равномерной толщины. Подход носит название Конструктивная сплошная геометрия (Constructive solid geometry | CSG), и его основной концепцией является возможность математического описания любых сложных объектов при помощи более простых. Простейшими телами в CSG являются примитивы – тела простой формы, такие как куб, сфера, цилиндр, призма. Более сложные объекты создаются при помощи применения булевых операций (объединение, пересечение, разность) к некоторому набору примитивов.
Пусть
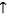 является разделителем параметров выдавливания.
является разделителем параметров выдавливания.Контуры выделяются из графов ребер проекций. В процессе инкрементального выдавливания один из контуров становится образующим, а второй – направляющим. Так как образующий контур и направляющий не должны быть параллельны, следующие операции выдавливания не выполняются :
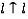 ,
, 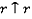 ,
, 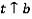 ,
, 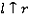 и т.д. , где f – front, R – rear, t – top, b – bottom, r – right, l – left. Кроме того, существует только шесть комбинаций пар проекций для процесса инкрементального выдавливания:
и т.д. , где f – front, R – rear, t – top, b – bottom, r – right, l – left. Кроме того, существует только шесть комбинаций пар проекций для процесса инкрементального выдавливания: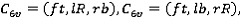
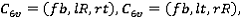
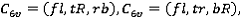
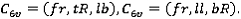
Инкрементальное выдавливание делится на три шага: сегментация образующих контуров в сегментные контуры, подсчет толщины выдавливания в направляющем контуре, совершение выдавливания.
В процессе инкрементального выдавливания учитываются только образующие контуры, внешние линии образующей грани. В начале находятся все точки поворота в направляющем контуре, затем они проецируются перпендикулярно на общую грань проекции. Эти точки используются для разделения образующего контура не несколько сегментных контуров. Результатом является матрица SGS:
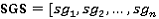 ],
],где
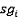 - i-ый сегментный контур,
- i-ый сегментный контур,n – количество сегментных контуров для выдавливания.
Расстояния между точками поворота вдоль направления выдавливания определяют толщину выдавливания: d-
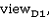 d-
d-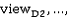 d-
d-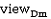 , где m – количество инкрементальных выдавливаний, d-
, где m – количество инкрементальных выдавливаний, d-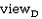 – инкрементальное расстояние для sgi-контуров для выдавливания вдоль направляющего контура.
– инкрементальное расстояние для sgi-контуров для выдавливания вдоль направляющего контура.В процессе самого выдавливания все сегментные контуры соединяются с толщинами выдавливания для того чтобы сформировать примитивные solid-объекты. Булева операция объединения примитивных solid-объектов затем создаст выдавленный solid.
В итоге для каждой пары проекций объединение всех примитивов создаст два выдавленных solid-объекта. К ним применяется операция пересечения, чтобы сформировать solid пересечения. Пересечение пересеченных solid-объектов для всех пар проекций создаст итоговый solid.
В 2005 году Jitendra Dimri и B Gurumoorthy в своей работе [8] описали алгоритм восстановления 3D моделей на основе объемов (volume-based). Их подход является ярким примером CSG подхода: изображение в формате DXF анализируется, и выделяются геометрические примитивы. Из примитивов создаются простейшие solid объекты, их существование перепроверяется. В конце к полученному набору solid объектов применяются булевые операции. Алгоритм Dimri и Gurumoorthy также обрабатывает вспомогательные проекции.
В работе рассмотрены основные подходы к восстановлению 3D псевдокаркасных моделей и solid объектов по заданным 2D проекциям.
Библиографический список
- Idesawa M. A System to Generate a Solid Figure from Three Views // Bulletin of Japan Society of Mechanical Engineers. 1973. № 16. P. 216-225.
- Wesley M. A., Markowsky G. Fleshing out Projections // IBM Journal of Research and Development. 1981. № 25 (6). P. 934-954.
- Sakurai, H. and Gossard, D. C.Solid model input through orthographic views // Computer Graphics (SIG- GRAPH’83). 1983. № 17. P. 243-252.
- Governi, L., Furferi, R., Palai, M., Volpe, Y. 3D geometry reconstruction from orthographic views: A method based on 3D image processing and data flitting // Computers in industry. 2013. № 64 P. 1290-1300.
- Bagali S., Warren J., Waggenspack N.A shortest path approach to wireframe to solid model conversion, in: Proceedings of the Third ACM Symposium on Solid Modeling and Applications // ACM, Salt Lake City, UT. 1995. P. 339–350.
- Aldefeld B.On Automatic Recognition of 3D Structures from 2D Representations // Computer Aided Design. 1983. № 15 (2). P. 59-72.
- Shum S. S. P., Lau W. S., Yuen M. M. F., Yu K. M. Solid Reconstruction from Orthographic Opaque Views Using Incremental Extrusion // Computer Graphics. 1997. № 26 (6). P. 787-800.
- Dimri J., Gurumoorthy B Handling sectional views in volume-based approach to automatically construct 3D solid from 2D views // Computer Aided Design. 2005. № 37. P. 485-495
