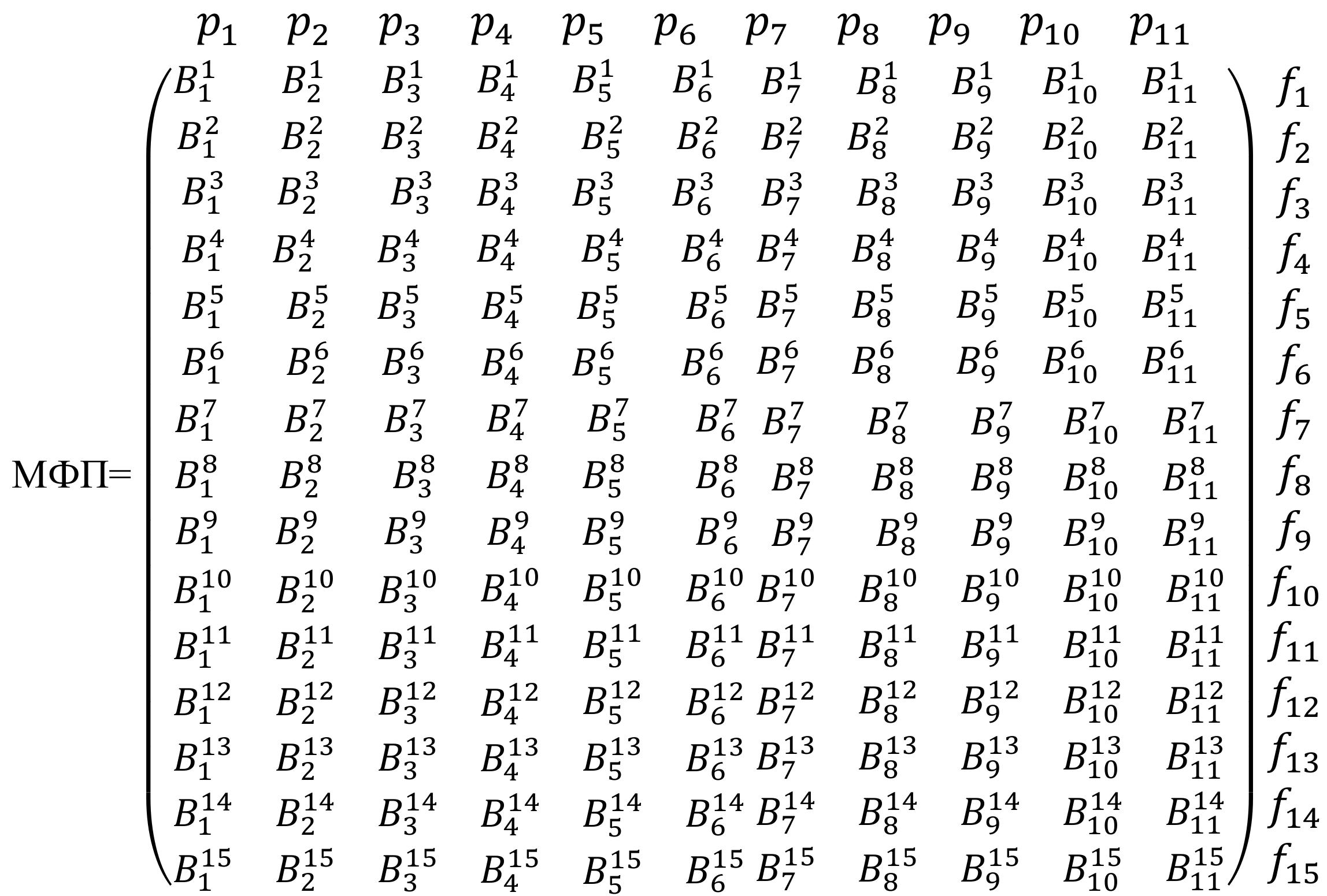При обработке канавок в глубоких отверстиях канавочным резцом происходит износ инструмента. Чтобы избежать этого нужно определить оптимальные режимы резания: скорость резания, подача, глубина резания и материал инструмента.
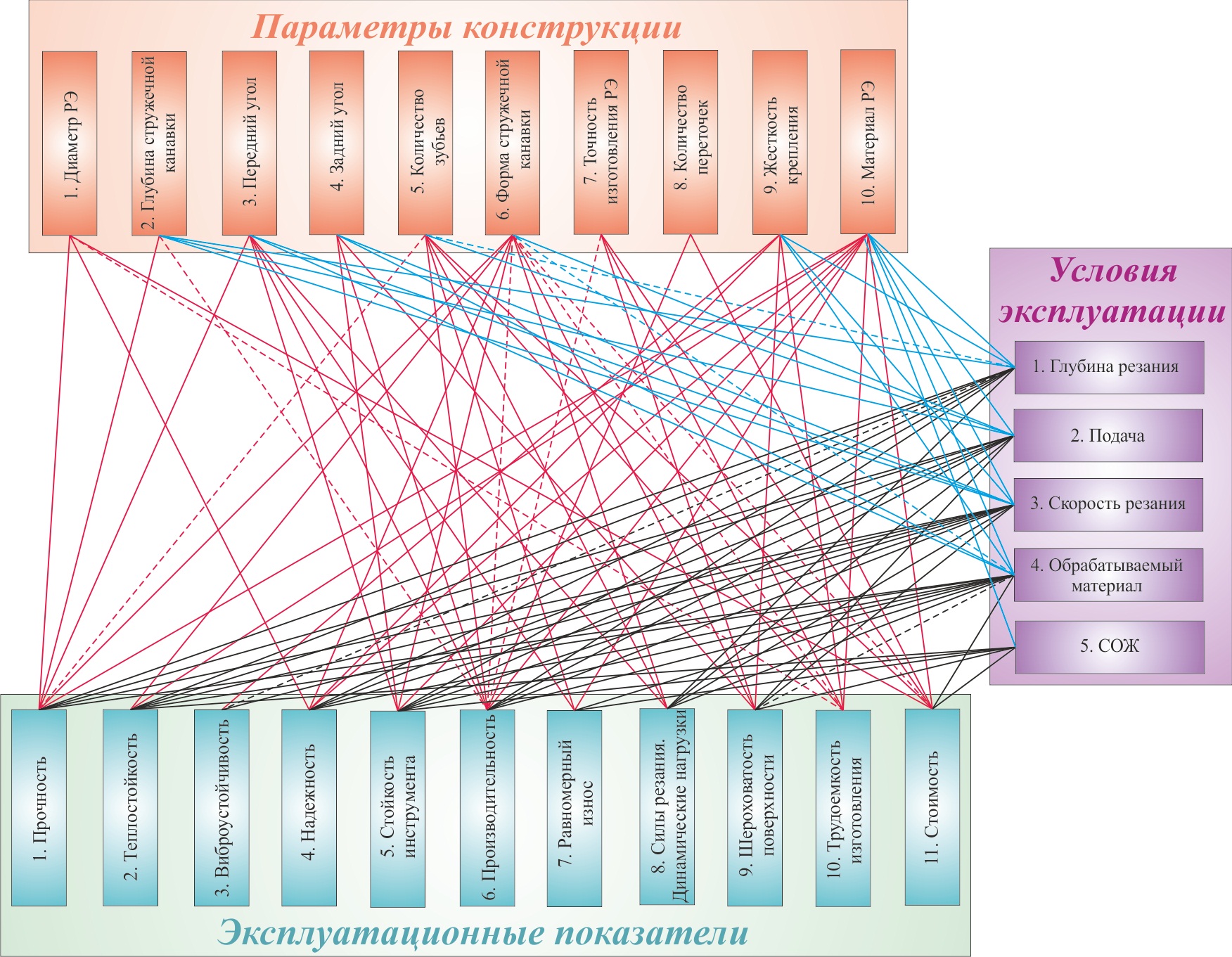
Проанализировав научную литературу[1-30], удалось определить,функциональные связи(ФС) между факторами процесса формообразования и между факторами и показателями процесса формообразования канавок в глубоких отверстиях канавочным резцом (рис. 1).
Улучшение показателей эксплуатации канавочного резца состоит в следующем: нужно выявить связь эксплуатационных показателей с условиями эксплуатации и параметрами конструкции, изучить эти связи и найти оптимальное решение для каждого показателя. Большую значимость при оценкеуровня формализации процесса формообразования имеет объем исследованных и установленных ФС между факторами и показателями процесса формообразования канавок в глубоких отверстиях канавочным резцом.
Рис. 1 Схема основных факторов и показателей процесса формообразования канавок в глубоких отверстиях канавочным резцом
Значение факторов, которые оказывают воздействие на процесс формообразования канавок, определяется уровнем их влияния на показатели, которые определяют характеристики инструмента и обрабатываемой детали. Также они влияют на технико-экономические и ряд других показателей.Основные ФС между факторами процесса формообразования канавок в глубоком отверстии канавочным резцом можно представить в виде матрицы МФ:
Такое представление необходимо для дальнейшегоиспользования ее при создании базы знаний процесса нарезания канавок в глубоком отверстии и получения на ее основе САПР специального инструмента–канавочного резца.
В математическом представлении матрицуможно представить так:
Аналогичным образом можно сформировать матрицу МФП функциональных связей между факторами и показателями процесса нарезания канавок и записать ее математически следующим образом:
Аij, Bij- элементы матрицы, которые в свою очередь включают в себя: совокупность функциональных зависимостей, различных табличных данных, сведений, связывающих между собой факторы процесса формообразования, расположенные в i–ой строке и j–ом столбце матрицы. Если функциональных связей нет, то элемент матрицы равны нулю.
На основании полученных матрицможно построить базу знаний процесса формообразования канавок в глубоком отверстии канавочным резцом. То есть их можно использовать в качестве некого интерфейса системы формирования и управления базой знаний процесса нарезания канавок, которая значительно упростит выбор оптимального инструмента. Каждый номер строки и столбца определенного элемента системы, который отличен от нуля, следуетиспользовать как уникальный адрес ячейки СУ базой данных, в которой хранятся все накопленные знания об установленных ранее функциональных связях. При создании САПР инструмента определяющимивходными данными будет являться набор показателей, которой удовлетворяет процессу формообразования канавок в глубоком отверстии канавочным резцом.
Рассмотрим на данном примере, как происходит решение конкретной задачи по созданию канавочного резца с наибольшей скоростью резания. f1 – f10 – это параметры конструкции, а f13 – это интересующий нас параметр- скорость резания.
Решение матрицы заключается в том, что необходимо рассчитать только значения одной 3 строки, которая будет соответствовать наибольшей скорости резания f13, которая в свою очередь зависит от параметров конструкции канавочного резцаf1 – f15.
 Задача станет сложнее при условии проектирования канавочного резца, который будет иметь не только наибольшую скорость резания, но и наибольшую глубинусрезаемого слоя. Таким образом, необходимо будет произвести расчет уже не одной, а двух строк: 1 и 3 строки.
Задача станет сложнее при условии проектирования канавочного резца, который будет иметь не только наибольшую скорость резания, но и наибольшую глубинусрезаемого слоя. Таким образом, необходимо будет произвести расчет уже не одной, а двух строк: 1 и 3 строки.
В данном случае необходимо сравнивать результат и его влияние на процесс обработки канавок в глубоком отверстии. И на основании полученных результатов выбрать оптимальное решение. Но это одна из простейших задач, а если попробовать рассчитать износостойкость инструмента? Износостойкость будет зависеть не только от конструкции, но и от условий эксплуатацииканавочногорезца. Следовательно, наша матрица тоже будет учитывать больше зависимостей.
В приведенной матрице р5 – износостойкость. Зависит она от таких параметров как передний и задний угол f4канавочного резца, материала режущего элемента f10, от условий эксплуатации – вида СОЖ f15 и т. д. При решении такого уравнения получается не один, а несколько результатов. И следует выбрать только те решения, которые оказывают наибольшее влияние на увеличение показателя износостойкости.
Наилучшим, то есть оптимальным решением такого уравнения будет вся область решений.
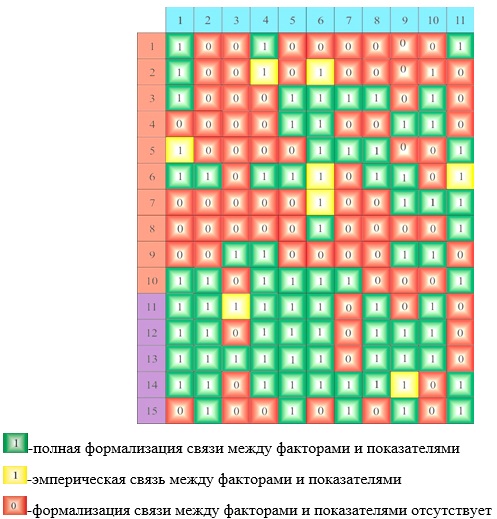
Используя вышеприведенные схемы функциональных связей путем преобразования построена матрица инцинденций, которая показывает установленныесвязи между факторами процесса формообразования (рис. 2), а также матрица инцинденций связей между факторами и показателями процесса формообразования канавок в глубоких отверстиях канавочным резцом (рис. 3).
Элементы матриц представлены в виде клавиш разных цветов. Цвета определяют степень формализации установленных функциональных связей.Элементы матрицы обозначены цифрой 1 в случае,когда присутствует связь, и 0 когда связи нет.
Рис. 2 Матрица функциональных связей между факторами
Рис. 3 Матрица функциональных связей между факторами и показателями
Данное представление полученной системы позволяет дать оценку степени формализации и качеству используемых функциональных связей при формообразовании канавок. Следовательно, в зависимости от начальных условий, можно сделать необходимый выбор, в состав которого входят факторы и функциональные связи между факторами и показателями процеса.
Вышеприведенные матрицы инцинденций могут служить основой в направлении дальнейших исследований процесса формообразования канавок в глубоком отверстии. Сами матрицы связей МФ и МФПбудут изменяться, так как будут изменения по составу факторов. Степень формализации связей тоже может варьироваться.
НИР поддерживается Федеральным государственным бюджетным учреждением «Фонд содействия развитию малых форм предприятий в научно-технической сфере».
Библиографический список
- Петухов Ю.Е. Формообразование численными методами / Ю.Е. Петухов. – М. : «Янус-К», 2004. – 200 с.
- Петухов Ю. Е., Домнин П. В. Формообразование фасонных винтовых поверхностей инструментов на основе применения стандартных концевых и торцевых фрез. – М.: ФГБОУ ВПО МГТУ «СТАНКИН», 2012. -130с.
- Гречишников, В.А. Математическое моделирование в инструментальном производстве/ Гречишников В.А., Колесов Н.В., Петухов Ю.Е. – М.: МГТУ «СТАНКИН». УМО АМ, 2003. – 116 с.
- Петухов Ю.Е. Проектирование инструментов для обработки резанием деталей с фасонной винтовой поверхностью на стадии технологической подготовки производства :дис. … докт. техн. наук : 05.03.01 / Петухов Ю.Е.. – М., 2004. – 393с.
- Петухов Ю.Е. Численные модели режущего инструмента для обработки сложных поверхностей / Петухов Ю.Е., Колесов Н.В. // Вестник машиностроения. – 2003. – №5. – С. 61-63.
- Петухов Ю.Е. Профилирование режущих инструментов среде Т-flexCAD-3D / Петухов Ю.Е. // Вестник машиностроения. – 2003. – №8. – С. 67-70.
- Петухов, Ю.Е. Способ формообразования фасонной винтовой поверхности стандартным инструментом прямого профиля / Петухов Ю.Е., Домнин П.В. // Вестник МГТУ «СТАНКИН». – 2011. – №3. – С. 102-106.
- Колесов Н.В. Система контроля сложных кромок режущих инструментов / Колесов Н.В., Петухов Ю.Е. // ИТО: Инструмент. Технология. Оборудование. – 2003. – №2. – С. 42-45.
- Петухов Ю.Е. Компьютерная модель формообразования сложной поверхности / Петухов Ю.Е., Домнин П.В. // Международная научно-техническая конференция «Автоматизация: проблемы, идеи, решения». В 2 т. : сб. науч. ст. – Тула, 2010. – Т. 1. – С. 197-200.
- Колесов Н.В. Компьютерная модель дисковых фасонных затылованных фрез / Колесов Н.В., Петухов Ю.Е., Баринов А.В. // Вестник машиностроения. – 1999. – №6. – С. 57-61.
- Домнин П.В. Решение обратной задачи профилирования на базе схемы численного метода заданных сечений /Петухов Ю.Е., Домнин П.В. // Справочник. Инженерный журнал с приложением. – 2011. – №11. – С. 26-29.
- Колесов Н.В. Математическая модель червячной фрезы с протуберанцем / Колесов Н.В., Петухов Ю.Е. // СТИН. – 1995. – №6. – С. 26-29.
- Колесов Н.В. Два типа компьютерных моделей режущего инструмента Колесов/ Н.В., Петухов Ю.Е. // СТИН. – 2007. – №8. – С. 23-26.
- Петухов Ю.Е. Точность профилирования при обработке винтовой фасонной поверхности / Ю.Е. Петухов, П.В. Домнин // СТИН. – 2011 – №7. – С. 14-17.
- Петухов Ю.Е., Математическая модель криволинейной режущей кромки спирального сверла повышенной стойкости / Ю.Е. Петухов, А.А. Водовозов // Вестник МГТУ «СТАНКИН». – 2012. – №3. – С. 28-32.
- Петухов Ю.Е. Некоторые направления развития САПР режущего инструмента / Ю.Е. Петухов // СТИН. – 2003. – №8. – С. 26-30.
- Петухов Ю.Е. Затачивание по передней поверхности спиральных сверл с криволинейными режущими кромками / Ю.Е. Петухов, А.А. Водовозов // Вестник МГТУ «СТАНКИН». – 2014. – №1 (28). – С. 39-43.
- Петухов Ю.Е. Определение задних кинематических углов при обработке винтовых фасонных поверхностей стандартными фрезами прямого профиля./ Петухов Ю.Е., Домнин П.В.// Вестник МГТУ Станкин. 2014. № 2 (29). С. 27-33
- Петухов Ю.Е. Задачи по формообразованию при обработке резанием /Петухов Ю.Е., Колесов Н.В., Юрасов С.Ю.// Вестник машиностроения. 2014. № 3. С. 65-71.
- Петухов Ю.Е. Компьютерное моделирование обработки винтовой канавки на заготовке концевой фрезы./ Петухов Ю.Е, Домнин П.В.// Известия Московского государственного технического университета МАМИ. 2011. № 2. С. 156-164.
- Петухов Ю.Е. Cпособ шлифования фасонных валов. Патент на изобретение RUS863310 04.05.1979
- Петухов Ю.Е. Устройство для правки фасонных шлифовальных кругов. Патент на изобретение RUS 823101 21.03.1979
- Петухов Ю.Е. Способ обработки цилиндрических поверхностей патент на изобретение RUS 904999 04.05.1979
- Петухов Ю.Е. Прибор для профилирования червячных фрез. Патентнаизобретение RUS 878467 07.12.1978
- Petukhov Yu.E. Some directions of cutting tool cad system development./Petukhov Yu.E.// Russian Engineering Research. 2003. Т. 23. № 8. С. 72-76.
- Petukhov Yu.E. Curvilinear cutting edge of a helical bit with uniform life./Petukhov Yu.E.// Russian Engineering Research. 2014. Т. 34. № 10. С. 645-648.
- Kolesov N.V. The mathematical model of a hob with protuberances./Kolesov N.V., PetukhovYu.E.// Russian Engineering Research. 1995. Т. 15. № 4. С. 71-75
- Petukhov Y.E. Shaping precision in machining a screw surface / Y.E. Petukhov, P.V. Domnin // Russian Engineering Research. – 2011. – T. 31. – №10. – С. 1013-1015.
- Kolesov N.V. Computer models of cutting tools / N.V. Kolesov, Y.E. Petukhov // Russian Engineering Research. – 2007. – T. 27. – №11. – С. 812-814.
- Petukhov Y.E. Determining the shape of the back surface of disc milling cutter for machining a contoured surface / Y.E. Petukhov, A.V. Movsesyan // Russian Engineering Research. – 2007. – T. 27. – №8. – С. 519-521.