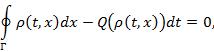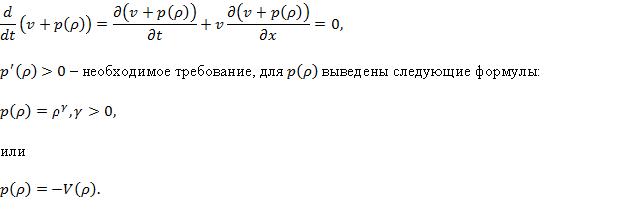Транспортные системы предназначены для обеспечения жизненно необходимых связей внутри города и между городами. С постоянно прогрессирующим увеличением транспортного потока, особенно в мегаполисах, многие транспортные системы, транспортные сети также нуждаются в улучшении собственной инфраструктуры и логистики. Потому особую важность приобретает оптимальное планирование транспортных сетей. При этом необходимо учитывать закономерности развития сети, распределение нагрузок на ее участки. Для решения таких задач необходимо применять математические модели.
Прежде всего стоит отметить, что из-за разнообразия и большого количества математических моделей трудно дать полную классификацию, учитывающую каждую модель. Потому, для упрощения, можно остановиться на следующих классах моделей, сгруппированным по их функциональной роли:
- Прогнозные модели;
- Оптимизационные модели;
- Имитационные модели[4].
Главная задача прогнозных моделей, как очевидно из названия, заключается в прогнозировании последствий при совершении изменений в транспортной сети. Существует, однако, большое количество имитационных моделей, которые предназначены для того, чтобы детально разобрать все детали движения, в том числе развитие процесса во времени. Так что можно сказать, что эти два класса моделей являются смежными, дополняющими друг друга. Говоря об оптимизационных моделях, следует отметить, что их используют для оптимизации функционирования транспортных сетей, прежде всего оптимизации маршрутов перевозок, выбора оптимальной конфигурации сети и т.д.
К классу имитационных моделей относится большое количество моделей, известных как модели динамики транспортного потока. Следует более подробно остановиться именно на них. Данные модели отличаются по своим задачам – от моделирования движения каждого отдельного автомобиля до моделирования движения транспортного потока в целом. Для ясности, данные модели делят на три общих класса:
- Модели-аналоги;
- Модели следования за лидером;
- Стохастические модели.
В моделях-аналогах движение АТС (автотранспортного средства) представляется в виде некоего физического закона. Большая часть моделей-аналогов являются газодинамическими или гидродинамическими моделями. Также такие модели называют макроскопическими, т.к. описывают динамику движения в целом.
Модели следования за лидером основаны на предположении о наличии прямой связи между перемещениями соседних АТС. Такие модели также называются микроскопическими. В них явно моделируется движение каждого АТС, что дает более точное описание движения по сравнению с макроскопическими моделями, но при этом эти модели требуют значительно больших затрат и вычислительных ресурсов.
В стохастических (вероятностных) моделях транспортный поток рассматривается как результат взаимодействия АТС на элементах транспортной сети. Закономерности таких взаимодействий также носят стохастический характер.
Микроскопические модели
- Модель оптимальной скорости Ньюэлла
- Модель следования за лидером GM
Одной из первых и простейших вариантов моделей следования за лидером является следующая модель, предложенная концерном General Motors:
- Модель Трайбера
Модели оптимальной скорости и следования за лидером возможно объединить в одну общую микроскопическую модель «разумного водителя»:
Гидродинамические модели
Особенностью данных моделей является допущение о том, что транспортный поток можно представить в виде одномерного потока жидкости со взаимнооднозначной зависимостью между скоростью потока и его плотностью.
- Модель Лайтхилла–Уизема–Ричардса (LWR)
В LWR-модели также допускается взаимнооднозначная зависимость между скоростью АТС и плотностью ТП, а также допускается выполнение закона сохранения АТС:
вогнутости функции. Это условие понимается так: движение по двум одинаковым и независимым дорожным полосам с разными плотностями менее предпочтительно, чем движение по этим же полосам с одинаковой плотностью, равной половине суммы первоначальных плотностей.
Закон сохранения массы интерпретируется как закон сохранения количества АТС. Получим уравнение:
которое справедливо для любого кусочно-гладкого контура Г. Стоит заметить, что данное соотношение справедливо и для разрывной функции, при этом под разрывом трактуется граница затора, характеризующееся резким увеличением плотности.
- Модель Танака
В данной модели также рассматривается однополосный транспортный поток.
- Модель Уизема
Данная модель отличается тем, что в ней учитывается «дальнозоркость» водителей, что подразумевает снижение скорости автомобиля при увеличении потока впереди и повышения скорости при его уменьшении.
Используется данное уравнение:
- Модель Пэйна
Эта модель отличается тем, что в ней не предполагается зависимость скорости потока от его плотности. Для скорости потока используется следующее уравнение:
откуда следует строгая гиперболичность системы. Для системы Пэйна неизвестно, как корректно определить глобальное по времени обобщенное решение. Но для строго гиперболической системы построена глобальная теория существования, единственности и устойчивости по начальным данным.
Существуют и недостатки данной модели. Например, при определенных значениях параметров могут возникать недопустимо большие плотности потока («бампер к бамперу»). Так что, изменив второе уравнение системы, можно избавиться от этого и некоторых других недостатков:
В заключении стоит отметить, что при моделировании транспортных потоков наиболее популярными являются модель LWR и ее аналоги, прежде всего за счет своей простоты в использовании. Более высоко уровневые модели, помимо своей трудности, требуют больших ресурсов, больших данных, больших затрат, тем самым зачастую нивелируя все свои преимущества. Модель LWR и ее аналоги, несмотря на свой возраст, остаются актуальными и на сегодняшний день.
Библиографический список
- Морозов И.И. и др. Численное исследование транспортных потоков на основе гидродинамических моделей // Компьютерные исследования и моделирование 2011 Т.3№ 4 с.389-412
- Лившиц В.Н. Автоматизация планирования и управления транспортными системами. М.: Транспорт, 1987.
- Семенов В.В. Математическое моделирование динамики транспортных потоков мегаполиса. – Изд-во: Институт прикладной математики им. М.В. Келдыша, 2004.
- Зеленина Л.И., Урыков В.А. Модели транспортного инфраструктурного комплекса // Современные научные исследования и инновации. 2014. № 12 [Электронный ресурс]. URL: http://web.snauka.ru/issues/2014/12/41692 (дата обращения: 09.12.2014)
- Швецов В.И. Математическое моделирование транспортных потоков. Автоматика и телемеханика. 2003, № 11. с.3-46
- Введение в математическое моделирование транспортных потоков: Учебное пособие / А.В.Гасников и др. – М.:МЦНМО, 2012. – 376с.