Главной отличительной чертой управляющей вычислительной системы (УВС) для управления динамическим объектом является наличие двух режимов: оперативного и неоперативного, обусловленных жесткими требованиями обработки большого количества информации в высоком темпе. Для обеспечения обработки информации на центральной вычислительной машине (ЦВМ), поступающей с датчиков объекта управления (ОУ) в заданном темпе, приходится распараллеливать вычислительные операции в подключаемых дополнительных специализированных вычислительных устройствах (СВУ). Такое разделение функций позволяет обеспечить нестационарный режим без нарушения темпа основного вычислительного процесса.
В реальном масштабе времени должны решаться две основные задачи: вычисление управляющего воздействия и интегрирование системы дифференциальных уравнений. Сведение системы дифференциальных уравнений к системе алгебраических уравнений в векторно-матричной форме удобно для ее реализации средствами цифровой вычислительной техники (ЦВТ) в СВУ, где должны выполняться операции «умножения с накоплением» одновременно над несколькими операндами [3,4].
Также в процессе управления переменные состояния могут принимать значения в широком динамическом диапазоне их изменения, поэтому обеспечить качество системы одним набором коэффициентов обратной связи не удается. Весь динамический диапазон разбивается на поддиапазоны. Нахождение переменной или всего вектора в некоторой зоне фазового пространства определят режим работы системы.
Процессор DSP (Digital Signal Processor) и нейропроцессоры обладая мощной вычислительной структурой, позволяет реализовать различные алгоритмы обработки информационных потоков. Сравнительно невысокая цена, а также развитые средства разработки программного обеспечения позволяют легко применять их при построении вычислительных систем с массовым параллелизмом [1, 8].
Ниже изложены принципы математического и алгоритмического обеспечения построения СВУ, реализующего идентификатор состояния системы управления гексаподом (HEX), позволяющего путем восстановления неизмеряемых координат вектора состояния и внешней нагрузки, повысить точность наведения оси верхней платформы.
Рассмотрим принцип действия СВУ. СВУ функционирует на основе информации [3,4]:
-
об измеряемой части вектора состояния HEX, которая снимается с датчиков;
-
о параметрах HEX;
- о законе движения HEX в виде вектора программы.
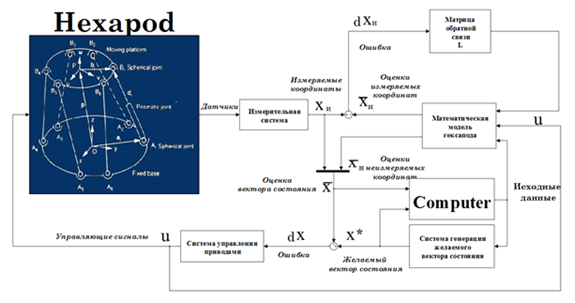
Рисунок 1 – Cистема управления HEX
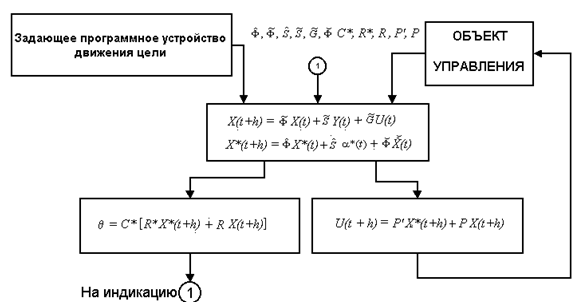
Рисунок 2 – Структура СВУ
Приняты следующие обозначения: — рабочие матрицы, полученные из матриц параметров HEX и матриц параметров корректирующих фильтров;
P‘, P — матрицы параметров корректирующих связей (6×100);
a*(t)— вектор-функция программы (18×1);
Y(t) — вектор-функция наблюдения (сигналы, поступающие от измерительной системы) (30×1);
X(t), X*(t) — вектор-функция текущего и программного состояния системы на i-м шаге управления (100×1);
X(t+h), X*(t+h) — то же на (i +1)-м шаге (100×1);
U(t) и U(t + h) — вектор управляющих воздействий на i-м и (i + 1)-м шагах управления (30×1);
h — шаг интегрирования (0.02) ;
Q — значение отклонения фокальной оси HEX от линии визирования объекта(3×1);
С*, R*, R — постоянные матрицы размерностью (3×3, 3×100, 3×100)
Из алгоритма управления HEX следует, что основной процедурой в СВУ является процедура умножения матрицы на вектор:
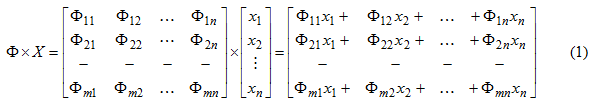
Одна компонента вектора результата получается суммированием произведения элементов строки матрицы на соответствующие элементы вектора — столбца. Эта последовательность операции повторяется столько раз, сколько строк в матрице. Для вычисления произведения матрицы на вектор необходимо выполнять

операций умножения,
где m — число строк матрицы;
n — число столбцов;
и Nсмв операций сложения, определяемых по формуле

операций сложения, или около 3000 пар операций умножение — сложение.
Исходя из заданного значения минимальной частоты расчета управляющих воздействия, максимально допустимое время выполнения одной пары операций умножение — сложение Tпо:

СВУ состоит из следующих основных функциональных блоков: устройства задания траектории цели, вычислителей управляющего воздействия по азимуту и углу места.
Вычислитель управляющего воздействия каждой оси наведения выполняет следующие функции:
- принимает от задающего устройства информацию о параметрах HEX и три компоненты вектора программы (угол, скорость, ускорение);
- принимает от устройства ввода информацию об измеряемой части вектора состояния от датчиков HEX;
- рассчитывает управляющее воздействие, обеспечивающее схождение наблюдателя к реальному объекту РТ;
- рассчитывает значения оценок не измеряемых компонент вектора состояния.
Согласно Рис. 1 цифровая система управления обеспечивает восстановление неизмеряемой части вектора состояния и формирование сигнала обратной связи по полному вектору состояния. Уравнения такого регулятора имеют следующий вид

где F,G — матрицы параметров наблюдающего устройства;
z(t) — вектор восстановленных переменных состояния;
y(t) — вектор измерений;
K1,K2 — коэффициенты обратной связи по состоянию.
Численное интегрирование дифференциальных уравнений наблюдающего устройства предлагается осуществлять путем их аппроксимации разностными уравнениями, позволяющими рассчитать значения восстановленного вектора состояния на интервалах времени, кратных шагу интегрирования.
Уравнения регулятора в векторно-разностной форме записываются в виде:
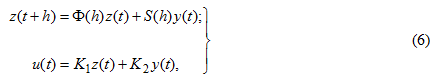
где Ф(h) — переходная матрица, характеризующая собственное движение;
S(h) — матрица, определяющая вынужденное движение наблюдающего устройства;
h — период квантования по времени (шаг интегрирования).
Матрицы Ф(h) и S(h) непосредственно зависят от величины шага интегрирования и определяются выражениями:
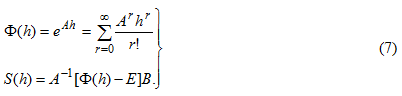
Согласно уравнениям (6) все вычисления в СВУ могут быть сведены к следующим операциям над массивами данных:
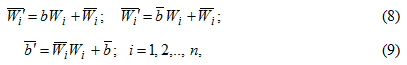
где b,W — скаляр и вектор, поступающие из базовой ЦВМ;
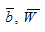 — скаляр и вектор, полученные на предыдущих операциях и хранящиеся в СВУ;
— скаляр и вектор, полученные на предыдущих операциях и хранящиеся в СВУ;
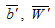 — результаты текущей операции;
— результаты текущей операции;
n — размерность векторов.
Так, например, умножение матрицы на вектор сводится к последовательности операций (8), где W представляет собой столбец матрицы множимого, b — компоненту вектора множителя. Частный случай умножения диагональной матрицы на вектор сводится к выполнению операций вида (11) при 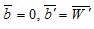 .
.
Для вычисления уравнений (6) в соответствии с операциями (8), (9) в СВУ в каждом такте из памяти извлекаются коэффициенты матриц Ф(h), S(h) упорядоченные по столбцам, а также матрицы-строки K1mK2 и с внешней шины данных выдается вектор измерений y(t). Также в СВУ хранятся значения вектора z(t) которые в процессе вычислений заменяются текущими результатами операций.
Наибольшая точность вычислений достигается при выполнении арифметических операций над числами с плавающей запятой. В ЦВМ с плавающей запятой диапазон изменения машинных переменных превышает размеры разрядной сетки за счет их искусственного преобразования, осуществляемого аппаратными или программными средствами. Это тождественно автоматическому выбору масштабных коэффициентов при выполнении каждой арифметической операции. Однако реализация в СВУ плавающей запятой существенно увеличивает время выполнения операций, что при решении задач управления в реальном времени практически не позволяет удовлетворить требования по быстродействию, предъявляемые к цифровым регуляторам. В связи с этим для обеспечения требуемого быстродействия арифметические операции в СВУ выполняются над числами с фиксированной запятой. При вычислении уравнений (8) в СВУ с фиксированной запятой могут возникать ситуации, когда машинного диапазона представления переменных и коэффициентов не хватает для получения результатов с требуемой точностью, т. е. переменные выходят за пределы разрядной сетки или принимают значения, соответствующие машинному нулю. В таком случае должны быть предусмотрены средства изменения масштабов для этих переменных, обеспечивающие удержание их в пределах заданного машинного диапазона.
В современных сигнальных процессорах (DSP) для повышения вычислительной мощности на одном кристалле размещаются несколько процессоров. В литературе такие многоэлементные процессоры получили название векторных или матричных. Данные процессоры имеют архитектуру, в который обрабатывается одиночный поток векторных команд и множественный поток данных (single instruction stream/multiple data stream — SIMD). Это позволяет выполнять одну арифметическую операцию сразу над многими числами (данными) – элементами вектора или массивами.
Как правило, такие многоэлементные процессоры содержат несколько процессоров с фиксированной запятой и один управляющий с плавающей, отвечающий за перемасштабирование. Управляющий процессор может самостоятельно вычислить плохо обусловленные операнды, либо организовать работу остальных процессоров на пересчет с двойной точностью. В первом случае не будет потери в быстродействии, так как вычисления будут произведены за один машинный цикл; во втором – вычисление произведения строки матрицы на вектор будет произведено больше чем за один машинный цикл. Поэтому необходимо произвести перемасштабирование операндов так, чтобы они все были хорошо обусловлены.
На этапе подготовки исходных данных все коэффициенты и переменные, входящие в систему уравнений (8), представляются в виде

где am— мантисса числа, по модулю меньшая единицы;
d — основание системы счисления;
p — порядок числа, округленного до целого.
С учетом этого систему уравнений можно записать так:
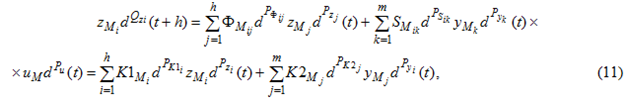
i=1,2,…,n
Обозначим порядки частных произведений

Нормировка матриц порядков частных произведений осуществляется построчно путем определения максимального элемента в каждой строке матрицы [P1, P2] и [R1,R2] и вычитания этого элемента из элементов строки. После такой нормировки старший порядок частных произведений становится нулевым, остальные — отрицательными. Нормировка матриц мантисс производится путем их перемножения с нормированными матрицами порядков.
В соответствии с описанным выше алгоритмом в СВУ для определения вектора мантисс Zm(t+h) в каждом такте передаются нормированные матрицы 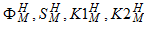 и вектор мантисс Ym(t). При выходе абсолютной величины мантиссы i-й переменной за границы заданного диапазона [Zmin,1] производится повторное определение мантисс и матриц порядков. Так, при превышении модуля Zmi на первом уровне порядок Pzi увеличивается на единицу или большую величину в зависимости от выбранной ширины диапазона изменения данной переменной в пределах одного масштаба. Увеличение порядка Pzi сопровождается повторной нормировкой соответствующих строк и столбцов матриц порядков частных произведений Р1, Р2, R1,R2 и последующим изменением нормированных матриц мантисс. Аналогичные действия производятся при выходе модуля мантиссы i-й переменной Zmi за нижнюю границу заданного диапазона. Только в этом случае порядок Pzi уменьшается на целую величину, что соответствующим образом учитывается в нормированных матрицах порядков и мантисс. Указанные действия адекватны замене переменной в системе уравнений (6) в результате изменения ее масштаба.
и вектор мантисс Ym(t). При выходе абсолютной величины мантиссы i-й переменной за границы заданного диапазона [Zmin,1] производится повторное определение мантисс и матриц порядков. Так, при превышении модуля Zmi на первом уровне порядок Pzi увеличивается на единицу или большую величину в зависимости от выбранной ширины диапазона изменения данной переменной в пределах одного масштаба. Увеличение порядка Pzi сопровождается повторной нормировкой соответствующих строк и столбцов матриц порядков частных произведений Р1, Р2, R1,R2 и последующим изменением нормированных матриц мантисс. Аналогичные действия производятся при выходе модуля мантиссы i-й переменной Zmi за нижнюю границу заданного диапазона. Только в этом случае порядок Pzi уменьшается на целую величину, что соответствующим образом учитывается в нормированных матрицах порядков и мантисс. Указанные действия адекватны замене переменной в системе уравнений (6) в результате изменения ее масштаба.
На рисунке 3 показана блок-схема разработанного алгоритма специального вычислительного устройства на базе нейропроцессора для управления гексаподом.
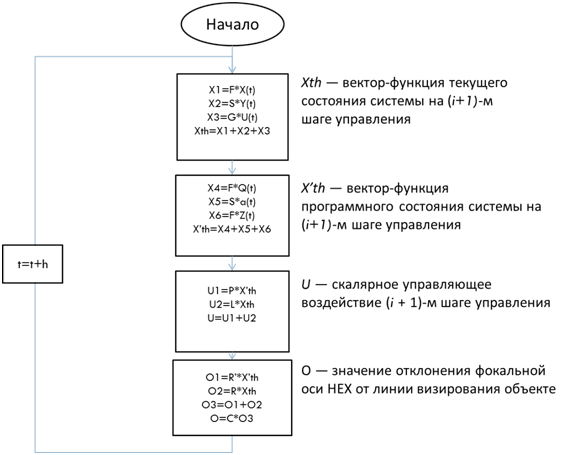
Рисунок 3 – Блок-схема алгоритма
В первом блоке вычисляется вектор-функция текущего состояние системы состоящая (Xth) из сумм произведений рабочих матриц полученных из матриц параметров гексапода и матриц параметров корректирующих фильтров в результате расчета (F, S, G), вектор-функций наблюдений(Y(t)), вектор-функций текущего и программного состояния системы (X(t)), и скалярного управляющего воздействия (U(t)). Во втором блоке вычисляется вектор-функция программного состояния системы (X’th) состоящая из сумм произведений рабочих матриц полученных из матриц параметров гексапода и матриц параметров корректирующих фильтров в результате расчета (F, S), вектор-функций текущего и программного состояния системы (Q(t), Z(t)), и
вектор-функция программы (a(t)). Третий блок отвечает за расчёт матрицы для скалярного управляющего воздействия (U), состоящего из суммы произведений матриц параметров корректирующих связей (P, L) и вектор-функций текущего и программного состояния системы (X’th, Xth). Последний блок отвечает за расчёт матрицы значений отклонений фокальной оси HEX от линии визирования объекта (O) состоящую из произведения постоянной матрицы (С) и вспомогательной матрицы (О3) которая состоит из суммы вспомогательных матриц (O1, O2) равных произведению постоянных матриц (R’, R) и вектор-функций текущего состояние системы и программного состояние системы на i+1 шаге управления (X’th, Xth).
Следует отметить, что вычисления, вызываемые изменением масштаба какой-либо переменной и связанные повторной нормировкой матриц порядков и мантисс, производятся не в каждом такте работы СВУ, а лишь тогда, когда мантисса этой переменной выходит за установленные пределы или когда порядок переменной на текущем шаге интегрирования отличается от порядка на предыдущем шаге. Это обеспечивает существенный выигрыш во времени по сравнению с выполнением операций с плавающей запятой.
СВУ предназначен для численного интегрирования матрично-векторной системы нелинейных дифференциальных уравнений с гладкими нелинейностями (sin, cos) в форме Коши с целью минимизации времени вычислений. Система уравнений описывает HEX или другой динамический объект имеющий следующие размерности векторов и матриц:
- Размерность системы: 100 уравнений первого порядка.
- Верхняя граница спектра собственных частот: 20 Гц.
- Вектор входных воздействий имеет размерность 30.
- Вектор выхода имеет размерность 20.
- Разрядность операндов 32 бита.
- Тактовая частота дискретизации 50 Гц.
Формирование матриц и векторов также должно осуществляться на СВУ, но в более медленном темпе и представляет отдельную задачу.
Обмен информацией между Базовой ЦВМ и СВУ происходит по согласованному протоколу временного сценария. Синхронизация обеспечивается СВУ.
Предложенная модель и алгоритм обеспечивают функционирование СВУ на базе нейропроцессора для управления динамическими объектами в реальном масштабе времени на примере гексапода.
Библиографический список
- Галушкин, А.И. Нейрокомпьютеры: Кн.3. – М: ИПРЖР, 2000. – 524 с.
- Горбань, А. Н. Нейроинформатика: кто мы, куда мы идем, как путь наш измерить // Вычислительные технологии. – 2000. – № 4. – С. 10-14.
- Городецкий А. Е., Тарасова И. JI. Нечеткое математическое моделирование плохо формализуемых процессов и систем СПб.: Изд-во Политехи, ун-та, 2010. С. 100-150.
- Городецкий А.Е., Козлов В. В., Артеменко Ю. Н., Тарасова И. Л. Вычисления в системах управления Учебное пособие СПб.: Изд-во Политехн. ун-та, 2006 С. 163-200.
- Злобин В.К., Григоренко Д.В., Ручкин В.Н., Романчук В.А. Кластеризация и восстанавливаемость нейропроцессорных систем обработки данных // Известия тульского государственного университета. Технические науки. – Тула : Издательство ТулГУ, 2013. – Вып.9. – Ч.2. – С.125-135.
- Комарцова, Л.Г., Максимов, А.В. Нейрокомпьютеры. – М.: Изд-во МГТУ им. Н.Э.Баумана, 2004. – 400 с.
- Романчук В.А. Инновационный программный комплекс моделирования вычислительных систем на базе нейропроцессоров “НейроКС” // Современные научные исследования и инновации. – Декабрь, 2012 [Электронный ресурс]. – URL: http://web.snauka.ru/issues/2012/12/19407.
- Романчук В.А. Моделирование нейропроцессорных систем // Отраслевые аспекты технических наук : научно-практический журнал. – Москва : ИНГН, 2013. – №10(34). – С.19-24.
- Романчук В.А., Ручкин В.Н. Оценка результатов моделирования вычислительных систем на базе нейропроцессоров // Известия тульского государственного университета. Технические науки. – Тула : Издательство ТулГУ, 2013. – Вып.9-2 – С.194-203.
- Романчук В.А., Ручкин В.Н. Разработка алгоритмов определения вида структуры нейропроцессорной системы на основе описания связей ее элементов // Информатика и прикладная математика : межвуз. сб. науч. тр. – Рязань : РГУ имени С.А.Есенина, 2011. – Вып.17. – С.106–109.
- Романчук В.А. Разработка алгоритмов определения связей элементов вычислительной структуры на базе нейропроцессоров // Информатика и прикладная математика : межвуз. сб. науч. тр. – Рязань : РГУ имени С.А.Есенина, 2011. – Вып.17. – С.102–105.
- Ручкин В.Н., Романчук В.А., Фулин В.А., Пролыгина А.А. Экспертная система нечеткой кластеризации нейропроцессорных систем // Известия тульского государственного университета. Технические науки. – Тула : Издательство ТулГУ, 2014. – Вып.6. – С.162-167.
