Робототехника, как отрасль научного знания и как основа промышленного производства, является инновационным направлением развития современного общества. Среди базовых аспектов применения роботов немаловажным считается их использование в труднодоступных местах, и местах, нахождение в которых небезопасно для человека. Примером могут служить роботы, перед которыми ставится задача по поиску и уничтожению взрывчатых веществ. В такой ситуации критичным является восприятие глубины для точной оценки расстояния до подозрительного объекта.
Рассмотрим основные виды зрения – монокулярное, бинокулярное и тринокулярное – с точки зрения восприятия глубины.
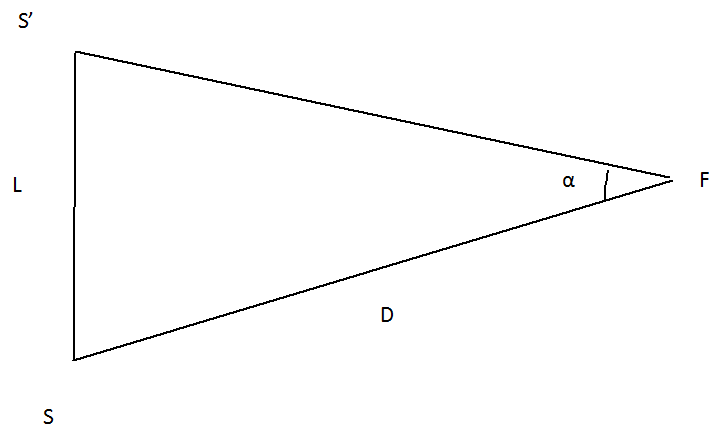
Монокулярное зрение опирается на единый источник информации об объекте. Если система, находящаяся в точке S, будет наблюдать объект F (рис. 1), то в таком случае оценить глубину и расстояние d до объекта, практически невозможно. Для этой цели можно использовать явление параллакса – явления, при котором при изменении положения наблюдателя S’ (рис. 1) меняется видимое положение объекта относительно фона. В таком случае расстояние d можно вычислить по формуле 1, где α – это угол изменения видимого положения объекта, а L – это расстояние, на которое смещается наблюдатель. Исторически сложилось так, что угол чаще всего измеряется не в радианах, а в угловых секундах.
Для малых значений угла a используется упрощенная формула 2.
Бинокулярное зрение ориентировано на наблюдение объектов двумя глазами. Наличие второго приемника информации позволяет более точно определить глубину, пространственное расположение и объемную форму наблюдаемых объектов. На рисунке 2 точки S1 и S2 обозначают приемники информации, а точки F1 и F2 – наблюдаемые объекты.
Для точного определения параметров объекта глаза располагают в одной плоскости, и зрение фокусируется так, чтобы зрительные оси пересекались в точке наблюдения (рис. 2). При этом получающийся угол (а1) называется углом конвергенции, а расстояние между глазами (b) – глазным базисом. Перефокусировка глаз при наблюдении второго объекта (F2) называется явлением аккомодации.
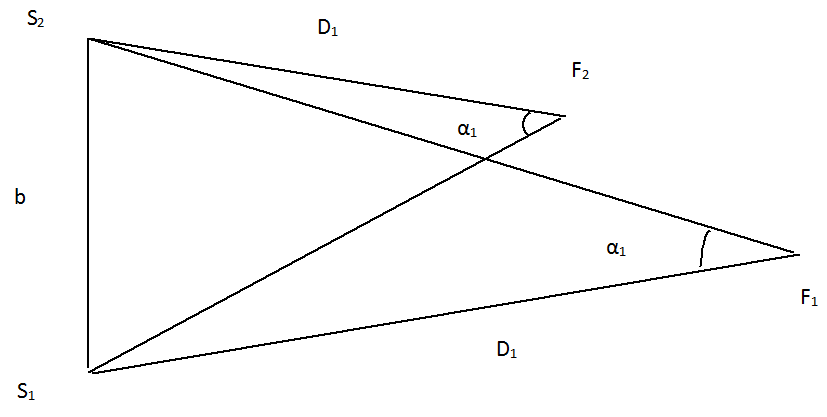 Рисунок 2. Оценка глубины при бинокулярном зрении
Рисунок 2. Оценка глубины при бинокулярном зренииТакже, при бинокулярном зрении появляется понятие его остроты или разрешающей способности, под которым понимают наименьшую разницу между углами конвергенции при явлении аккомодации, когда система способна вычислить или воспринять ΔD.
Определим параметры восприятия глубины при бинокулярном зрении. В общем случае можно воспользоваться формулой 2.
Будем использовать формулу 3 для определения параметров оценки глубины при бинокулярном зрении и монокулярном зрении с учетом смещения. Рассмотрим сначала базовые параметры оценки глубины человеческого зрения. Стандартным глазным базисом человека является величина в 65 мм, а острота зрения – 20’’.
При D = 25 см (расстояние, на котором происходит чтение текста) ΔD будет равняться 0,1 мм.
![]()
При D = 100 м ΔD будет равняться 0,1 м [1].
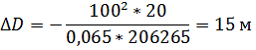
Теперь оценим параметры тринокулярного зрения (рис. 3). На рисунке 3 точки S1, S2 и S3 обозначают приемники информации, х – расстояние от S3 до плоскости, а точки F1 и F2 – наблюдаемые объекты.
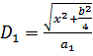 ,
,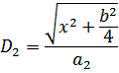
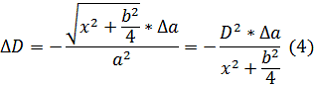
Возьмем х=1 м, остальные параметры оставим неизменными. Тогда ΔD будет равняться 0,97 м.
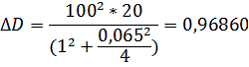
Другими словами, восприятие глубины при наличии третьего источника информации, находящегося над плоскостью на расстоянии 1 м значительно повысится.
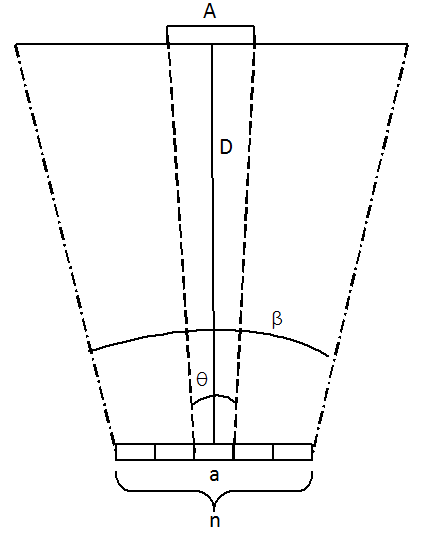
Теоретические расчеты не учитывают специфику матриц системы зрения, точнее их разрешающую способность и угол обзора. Рассмотрим проекцию изображения на плоскую матрицу, состоящую из n дискретных элементов зрения шириной a и углом обзора β. Некоторый объект шириной A, расположенный в параллельной относительно матрицы плоскости, проецируется на элемент матрицы с расстояния D целиком (рис. 4).
С уменьшением D проецируемый объект будет проецироваться не только на исходный элемент матрицы, но и на соседние элементы, т.е. его можно будет рассмотреть более точно. При увеличении D тот же объект будет проецироваться только на часть элемента матрицы, совместно с объектами, прилегающими к нему в проекции. Так можно определить предельное расстояние, которое зависит от разрешения матрицы и ее угла обзора, на котором объект еще различим матрицей:
Для бинарной системы смещение объекта на a в проекции объекта одного окуляра по отношении проекции другого окуляра гарантирует распознавание глубины объекта шириной A с расстояния D (рис. 5). Если смещение происходит на меньшую величину, то определение глубины становится затруднительным.
Учитывая разрешение матриц зрения и базис b системы получим зависимость расстояния, на котором возможно определить глубину объекта, если он сместился на k элементов матрицы (начальное положение от начала матрицы m):
.gif) (6)
(6)В тринокулярной системе качество восприятия глубины очевидным образом зависит от взаимного размещения окуляров: на одной горизонтальной оси (с равными или неравными промежутками), в углах равностороннего, равнобедренного, прямоугольного или произвольного треугольника. Очевидно, что несимметричные конструкции дают преимущество одному полю зрения (справа или слева), что нецелесообразно. Размещение трех окуляров на горизонтальной прямой не решает проблем с оценкой расстояний до протяженных объектов параллельных горизонту. Наилучшей способностью к оценке глубины и разрешению проблем бинокулярного зрения будет иметь система в форме равнобедренного треугольника. В такой конфигурации оба поля зрения не имеют преимущества друг перед другом.
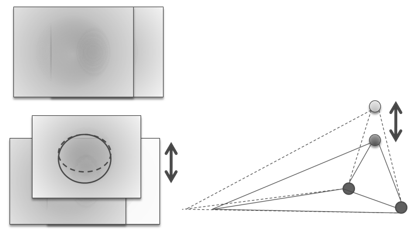
Очевидно, что перемещение третьего окуляра вдоль высоты треугольника увеличивает (при движении вверх) способность системы к оценке большей глубины или снижает (при движении вниз), рис. 6.
С другой стороны область наилучшего видения находится в обратной зависимости от увеличения способности оценки глубины. Учитывая краевые эффекты проекций получим, что области наилучшего видения будет смещаться вверх, сжимаясь и вниз растягиваясь.
Дополнительно при оценке глубины возникает еще одна проблема – проблема переднего плана. Объекты переднего плана не могут распознаваться n-окулярными (n>1) системами по полученным с матриц окуляров изображений, т. к. изображения объектов переднего плана достаточно сильно разнятся. На одном из окуляров изображение вообще может отсутствовать. Поэтому фактически невозможно вычислить расстояние до таких объектов. Такая же проблема возникает с объектами, находящимися на краях поля зрения системы. Решить эту проблему убедительно можно только при помощи параллакса одного из окуляров.
Библиографический список
- Курс лекций по фотограмметрии МИИГАиК // Проект Вики — Фотограмметрия. URL: http://www.racurs.ru/wiki/index.php/Курс_лекций_по_фотограмметрии_МИИГАиК (дата обращения: 01.11.2015).