Рассматриваемый беспилотный летательный аппарат (БПЛА) Т-10 представляет собой высокоплан, построенный по нормальной двухкилевой аэродинамической схеме, с неподвижным относительно корпуса крылом, динамически подобный самолету СУ-27 и выполненный в масштабе 1:5. Он предназначен для целенаправленного управляемого движения в пределах атмосферы на различных, в том числе и малых, высотах полета на основе использования аэродинамического принципа полета и создания аэродинамических управляющих моментов.
Приведем краткую характеристику анализируемого объекта.
Для применения в учебном процессе модель Т-10 была закреплена на управляемом трёхмерном подвесе [1] (рис. 1 ).
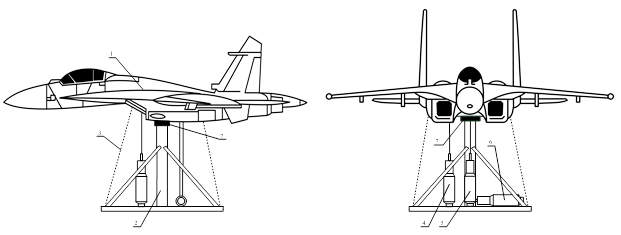
Рисунок 1. Кинематическая схема трёхмерного подвеса стенда
Подвес состоит металлического каркаса (2), на котором закреплён БПЛА (1), Нейтральное положение объекта управления обеспечивается благодаря балансировочным пружинам (3), изменение углов тангажа, крена и рыскания модели происходит при помощи приводов РАУ-107А (4,5,6). Так же на подвесе расположен блок потенциометрических датчиков (7), который позволяет обеспечить обратную связь по угловому положению БПЛА относительно трёх осей координат.
Измерительный блок на борту БПЛА состоит из гироскопических датчиков углов (ДУ) курса, крена и тангажа, датчиков угловых скоростей (ДУС) (по два датчика, относительно каждой из осей связанной с объектом системы координат) и расположен в центре масс летательного аппарата.
Для сбора и преобразования к цифровому виду выходных сигналов аналоговых датчиков служит модуль аналого-цифрового преобразования.
Основной контроллер осуществляет обмен данными между моделью и персональным компьютером-сервером и предназначен для управления рулевыми агрегатами и бортовыми сервоприводами, расположенными на подвесе. Он выступает в роли вычислительного устройства и задает закон углового движения БПЛА.
Предусмотрен двухсторонний обмен данными между персональным компьютером-сервером и компьютерами-клиентами по каналу беспроводной связи, организованного при помощи соответствующей системы. Клиенты получают данные с датчиков в реальном масштабе времени.
Ручное управление положением модели осуществляется при помощи джойстика, который подключен к компьютеру-серверу.
Особенности исполнения стенда на базе БПЛА Т-10 сформировали ряд направлений углубленной подготовки студентов при проведении практических и лабораторных занятий. Это связано, в первую очередь, с относительно большими массо-габаритными размерами модели (масса порядка 150 кг., длина – 4,05м. и размах крыльев – 2,7м.). Во вторую очередь – небольшой ход штока привода не дает возможности получать значительные углы движения Т-10. Поэтому, такой вариант крепления на кардановом подвесе вносит определенную инерционность и обуславливает колебательный характер движения модели. С другой стороны, применение штатных датчиков и проведение анализа заведомо не оптимального движения объекта как раз и позволяет приобретать определенные практические навыки.
Остановимся на некоторых из них.
В качестве примера, рассмотрим продольное движение модели при подаче ступенчатого управляющего сигнала, а для анализа выберем угол тангажа ϑ(t)и его угловую скорость ωϑ(t).
Диаграммы сигналов приведены на рис. 2.
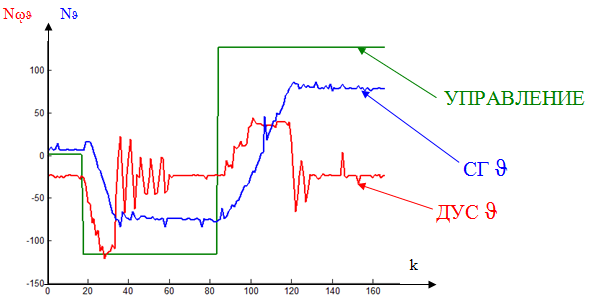
Рис. 2. Диаграммы сигналов управления и с датчиков
Анализ полученных результатов показывает, что их непосредственное использование затруднительно, в следствии наличия значительных помех и шумов. Отсюда вытекает первое направление, которое в общем случае содержит:
- напоминание о принципах построения фильтров;
- проектирование фильтра для постсеансовой обработки данных;
- проектирование фильтра для обработки данных в масштабе реального времени;
- проверка фильтров на выходных сигналах датчиков модели;
- сравнение результатов работы фильтров.
Для дальнейшей обработки применим экспоненциальный фильтр скользящего среднего второго порядка с двумя одинаковыми частотами среза, который определяется следующим уравнением [2,с 203]:
y1вых(k) = α* y1вых(k-1) + (1- α)*yвх(k),
y2вых(k) = α* y2вых(k-1) + (1- α)*y1вых(k),
где y1вых – сигнал на выходе первого фильтра;
y2вых– сигнал на выходе первого фильтра;
yвх – сигнал на входе фильтра;
α – весовой коэффициент, который примем равным 0,9;
k – номер отсчета входной-выходной последовательности.
Отфильтрованные показания датчиков угла и угловой скорости приведены на рис. 3.
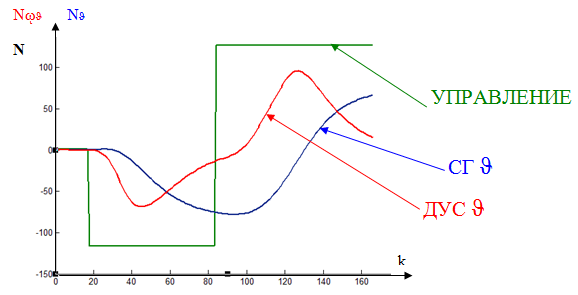
Рис. 3. Отфильтрованные показания датчиков угла и угловой скорости.
Отфильтрованные показания датчика угла могут использоваться для практической отработки следующих направлений:
- определение статической характеристики ДУ;
- постобработка и обработка результатов эксперимента для ДУ в реальном масштабе времени;
- практический переход от показаний ДУ к значениям угловой скорости;
- получение вектора угловой скорости и его компонент по временным характеристикам угловых параметров и сравнение с реальными значениями угловых скоростей.
Для примера, используем [3,с.47] известные соотношения - вычисления угловой скорости из значений угла или в дискретной форме
yвых(k) = (yвх(k) - yвх(k-1))/ΔТ,
где:
k – номер текущего шага;
yвых(k) - значение производной от входного сигнала на шаге k;
yвх(k) - значение входного сигнала на текущем шаге k;
yвх(k-1)- значение входного сигнала на предыдущем шаге k-1;
ΔТ - приращение времени на текущем шаге.
Проведем дифференцирование показаний датчика угла и получим значения угловой скорости угла тангажа. Эти результаты приведены на рис.4.
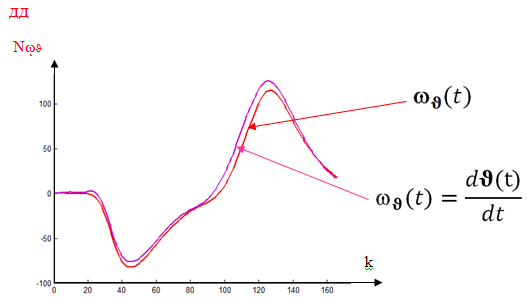
Рис. 4. Диаграммы измеренных и вычисленных значений угловой скорости.
Аналогично углу, данные с датчика угловой скорости могут использоваться, например, для решения следующих практических задач:
- определение статической характеристики ДУС;
- постобработка и обработка результатов эксперимента для ДУС в реальном масштабе времени;
- практический переход от показаний ДУС к значениям углов;
- получение углов ориентации корпуса объекта по значениям угловой скорости и сравнение с реальными значениями углов.
Так, с учетом [3,с.50]известных соотношений 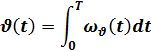 - вычисления угла из значений угловой скорости или в дискретной форме:
- вычисления угла из значений угловой скорости или в дискретной форме:
yвых(k) = yвых(k-1) + yвх(k-1)*ΔТ,где:
k – номер текущего шага;
yвых(k) - значение интеграла на шаге k;
yвых(k-1) - значение интеграла на предыдущем шаге k-1;
yвх(k-1)- значение подынтегральной функции на предыдущем шаге k-1;
ΔТ - приращение времени на текущем шаге,
определим значения угла тангажа из показаний датчика угловой скорости.
Результаты измерений и вычислений приведены на рис. 5.
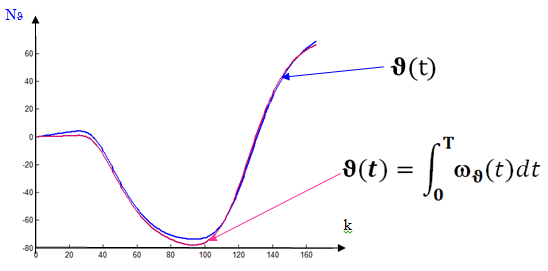
Рис. 5. Диаграммы измеренных и вычисленных значений угла тангажа.
И в заключение отметим, что особый интерес вызывает использование стенда для таких направлений углубленной подготовки:
- сравнительный анализ показаний датчиков для определения их работоспособного состояния с учетом взаимных расчетов угла из угловой скорости и наоборот;
- идентификация математической модели объекта с учетом действия реальных возмущающих воздействий.
Библиографический список
- Патент на корисну модель «Автоматизований дослідницький комплекс безпілотного літального апарата»UA 76187 від 25.12.2012 МПК B64C 13/00 (2012.01).
- Густав О., Джангуидо П. Цифровые системы автоматизации и управления. – СПб.: Невский Диалект, 2001. – 557с.: ил.
- Вадутов О.С. Математические основы обработки сигналов. Практикум: уч. пособ./О.С. Вадутов Томский политехнический университет. – 3-е изд., испр. и доп. – Томск: Изд-во Томского политехнического университета, 2014. – 102 с.


