Введение
В чем же суть специальности по управлению в технических системах? Учат как будто всему и ничему конкретно. Дополнительно к теории управления дают программирование, но не готовят программиста; читают схемотехнику, но не так глубоко как для электронщика, знакомят с конструированием, физикой, математикой и другими предметами, но как они связаны со специальностью?
Попробуем взглянуть на задачу построения идеальной системы управления и на необходимость “смежных” знаний. В этой работе затронуты следующие вопросы. Передаточная функция и ее преобразование во временную и частотную области. Идеальная система управления. Обратная связь и устойчивость системы. Влияние запаздывания. Неустойчивость петлевых вычислений. Средства реализации функций управления. Дано описание действующих авторских систем: автоматического переключения водных потоков на солнечной энергии без использования солнечных батарей и пассивной системы минимизации усилия открывания люка.
Передаточная функция
Известно, что модели систем и их составляющих, используемых при анализе и синтезе линейных систем управления, можно представить в виде
- дифференциальных уравнений;
- передаточных функций;
- временных или частотных характеристик.
Передаточная функция равна отношению изображений по Лапласу переменных выхода Y(s) и входа F(s) при нулевых начальных условиях.

Рис. 1. Передаточная функция.
На вход системы подаётся сигнал F(s) – требуемое состояние в котором должна находиться система, с выхода получают информацию о текущем состоянии в котором система находится на самом деле Y(s) – реакция системы (Рис. 1). Например (Рис. 2), от привода могут потребовать чтобы он находился в заданной координате F(s) в момент его нахождения в текущей координате Y(s). По величине рассогласования e(s) = F(s) – Y(s) регулятор Wr(s) формирует управляющее воздействие на трансмиссию Wo(s) с целью перемещения привода (перевода системы) из текущего состояния в заданное.
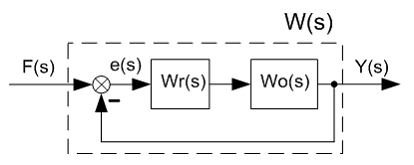
Рис. 2. Пример детализации передаточной функции W(s) – разбиения ее на множество функций подсистем и узлов и связей между ними.
Поскольку на выполнение любой работы требуется время, то достижение цели Y реальной системой всегда отстаёт от момента задания цели F. Вид переходного процесса Y (реакция системы) может значительно отличаться от входного воздействия F (Рис. 3).
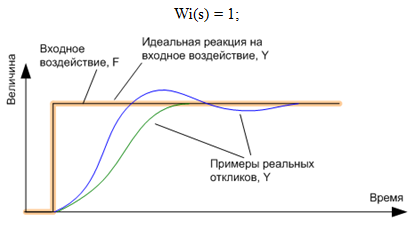
Рис. 3. Примеры реакции (откликов) системы на ступенчатое воздействие. Идеальной отклик повторяет входное воздействие.
Как должна выглядеть передаточная функция идеальной системы Wi, в которой реакция Y мгновенно повторяет заданное воздействие F? Ответ достаточно прост – передаточная функция должна равняться единице.
Идеальная система управления
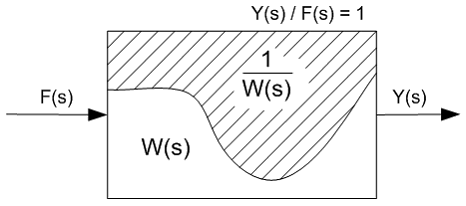
Для построения идеальной системы управления необходимо исходную систему с передаточной функцией W(s) дополнить обратной функцией 1/W(s) так, чтобы суммарная передаточная функция стала равной единице:

Рис. 4. Получение передаточной функции идеальной системы.
К сожалению, идеальное решение на практике не реализуемо, но приближение к нему является достойной задачей специалистов по управлению.
Преобразования дифференциальное уравнение <> передаточная функция <> частотные характеристики
Передаточная функция легко записывается по дифференциальному уравнению заменой производной d/dt на ![]() . Обратной заменой можно найти эквивалентное дифференциальное уравнение. Например, преобразования операторной формы апериодического звена
. Обратной заменой можно найти эквивалентное дифференциальное уравнение. Например, преобразования операторной формы апериодического звена ![]() в дифференциальное уравнение выглядит следующим образом.
в дифференциальное уравнение выглядит следующим образом.
Для компьютерного решения дифференциального уравнения необходимо из непрерывной области d/dt перейти в дискретную область: ![]() . Реакция на ступенчатое воздействие f(t)= 1(t), для t>0 и y=0 при t=0 (нулевых начальных условиях) вычисляется в следующей последовательности.
. Реакция на ступенчатое воздействие f(t)= 1(t), для t>0 и y=0 при t=0 (нулевых начальных условиях) вычисляется в следующей последовательности.
.gif) 1. ;
1. ; .gif) ;
; .gif) 2. ;
2. ;.gif)
.gif)
- Далее, повтор со 2-го шага.
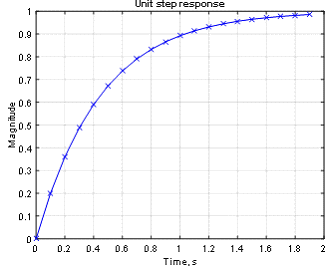
Например, для T=0.5; k = 1; и ![]() переходный процесс, выполненный в МатЛАБ, выглядит как показано на Рис. 6.
переходный процесс, выполненный в МатЛАБ, выглядит как показано на Рис. 6.
%m-код алгоритма с отображением переходного процесса:
| T= 0.5; k = 1; dt=0.1; i = 1; time(i) = 0; y(i) = 0; while i < 20 i = i+1; dy = (k-y(i-1))*dt/T; y(i) = y(i-1)+dy; time(i)=(i-1)*dt; end figure plot(time,y,‘b’); hold on plot(time,y,‘xb’); grid on; xlabel(‘Time, s’); ylabel(‘Magnitude’); title(‘Unit step response’); |
 |
Для перехода в частотную область необход оператор s заменить произведением j![]() , где j – мнимая единица;
, где j – мнимая единица; ![]() - круговая частота в рад/c. Комплексная частотная характеристика апериодического звена:
- круговая частота в рад/c. Комплексная частотная характеристика апериодического звена:
Чтобы получить Амплитудно-Фазовую Частотную Характеристику (AФЧХ) необходимо сначала из комплексной функции выделить вещественную и мнимую части. В случае апериодического звена это можно сделать умножением числителя и знаменателя на ![]() :
:
а затем получить выражения для модуля и фазы частотных характеристик (АЧХ и ФЧХ):
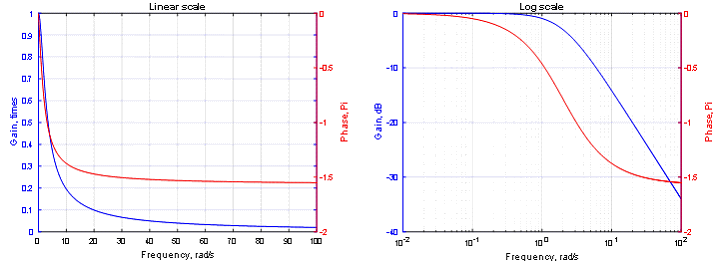
АФЧХ апериодического звена показана на Рис. 7 слева. Перевод частоты и амплитуды в логарифмический масштаб (функциями log10 и 20log10 соответственно) позволяет упростить построение частотных характеристик последовательного соединения звеньев (Рис. 7, справа). Так, в линейном пространстве коэффициенты передачи звеньев необходимо перемножать, а в логарифмическом – складывать. Последнее легко можно выполнить графическими средствами.
%m-код построения АФЧХ:
T= 0.5; k = 1; dt=0.1;
w = 0.01:0.01:100;
R = k./sqrt((T*w).^2+1)
F = -atan(T*w);
if 1
figure
[AX,H1,H2] = plotyy (w,R,w,F);
hold(AX(1));
hold(AX(2));
YLim_left = get(AX(1),‘YLim’);
set(AX(1),‘YTick’,YLim_left(1):0.1:(YLim_left(2)));
set(AX(1),‘YColor’,‘b’);
set(H1,‘Color’,‘b’);
set(H1,‘LineWidth’,1);
YLim_right = get(AX(2),‘YLim’);
set(AX(2),‘YTick’,YLim_right(1):0.5:(YLim_right(2)));
set(AX(2),‘YColor’,‘r’);
set(H2,‘Color’,‘r’);
set(H2,‘LineWidth’,1);
grid
set(get(AX(2),‘Ylabel’),‘String’,‘Phase, Pi’)
set(get(AX(1),‘Ylabel’),‘String’,‘Gain, times’)
xlabel(‘Frequency, rad/s’);
title (‘Linear scale’);
end
%для построения в логарифмическом масштабе:%R = 20*log10(R); set(AX(1),’XScale’,'log’); set(AX(2),’XScale’,'log’);
Обратная связь и устойчивость системы
Обратная связь вводится с целью улучшения характеристик разомкнутой системы (без обратной связи). Обратная связь позволяет на порядок улучшить такие параметры как быстродействие, точность, стабильность, энергопотребление.
Пример увеличения быстродействия системы с сохранением ее стабильности при замыкании единичной обратной связью и увеличением коэффициента передачи в 10 раз приведен на Рис. 8. Моделирование выполнено в среде Simulink.
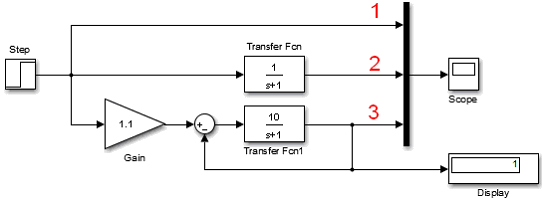
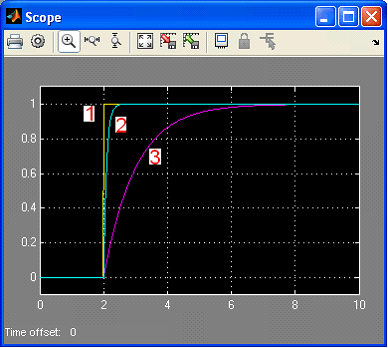
Рис. 8. Реакция звеньев (2 и 3) на ступенчатое воздействие (1). Увеличение быстродействия замыканием обратной связью и увеличением коэффициента усиления.
Необходимо помнить, что обратная связь без настройки системы может и ухудшить характеристики замыкаемой системы, например, вызвать перерегулирование (превышение заданной координаты) там где это недопустимо, см. Рис. 9, и даже привести к потере функциональности, как это показано в виде расходящегося процесса на Рис. 10.
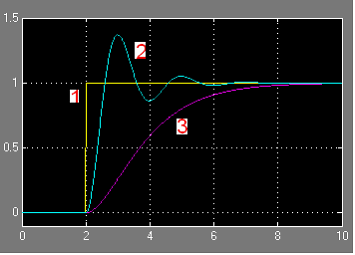
Рис. 9. Пример влияния замыкания обратной связью на динамические характеристики системы. Сигнал 2 – реакция разомкнутой системы 1/(S2+2S+1) на единичное ступенчатое воздействие (сигнал 1). Сигнал 3 – реакция замкнутой системы.
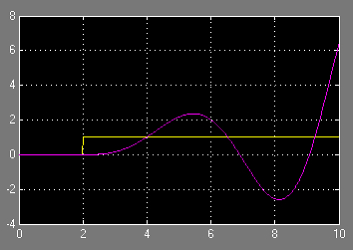
Рис. 10. Пример неустойчивого процесса: реакция системы 1/(S3+S+1) на единичное ступенчатое воздействие.
Вышеприведённые примеры переходных процессов показывают, что системы с обратной связью необходимо исследовать на устойчивость, оценить влияние замыкания обратной связью на изменение динамических характеристик системы. Одним из таких методов является оценка устойчивости по Амплитудно – Частотным Характеристикам (Рис. 11).
Для определения устойчивости системы по ее реакции необходимо ко входу системы приложить сигнал, спектр которого перекрывает полосу пропускания исследуемой системы, например, сигнал из следующего ряда типовых воздействий [1].
Единичная -функция f(t)= (t), F(s)=1.
Единичное ступенчатое воздействие f(t)= 1(t), F(s)=1/s.
Линейно нарастающий сигнал, или – воздействие с постоянной скоростью f(t)= at, F(s)=a/s2.
Воздействие с постоянным ускорением f(t)= at2/ 2, F(s)=a/s3.
Влияние запаздывания на устойчивость
В полосе пропускания в которой коэффициент передачи (модуль) больше единицы, фазовая характеристика разомкнутой системы не должна превышать 180 градусов – граничное значения устойчивости замкнутой системы в которой наблюдаются автоколебания. Для устранения автоколебаний с сохранением устойчивости, необходимо на частоте среза ![]() обеспечить запас по фазе (см Рис. 11).
обеспечить запас по фазе (см Рис. 11).
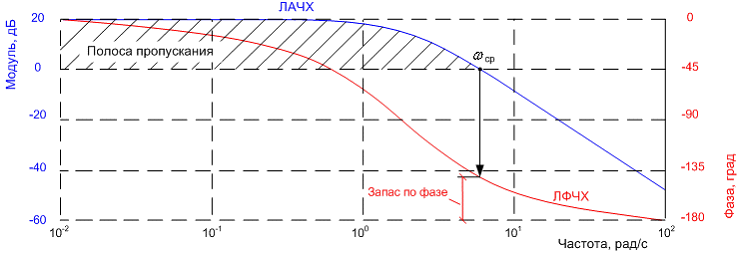
Рис. 11. Логарифмические характеристики, полоса пропускания, частота среза ![]() и запас по фазе.
и запас по фазе.
Фазовая характеристика показывает насколько смещается гармоника (синусоидальный сигнал соответствующей частоты ) проходя по контуру (замкнутой петле). На Рис. 12 показан пример увеличения рассогласования (розовый сигнал) с ростом запаздывания синего сигнала относительно зеленого. Частота и амплитуда зеленого и синего сигнала совпадают. Видно, что при больших запаздываниях сигнал рассогласования превышает амплитуду исходного сигнала.
Tmax = 20;
dt = 0.01;
time = 0:dt:Tmax;
phase = time.*(pi/Tmax);
S1 = sin(2*pi*time);
S2 = sin(2*pi*time+phase);
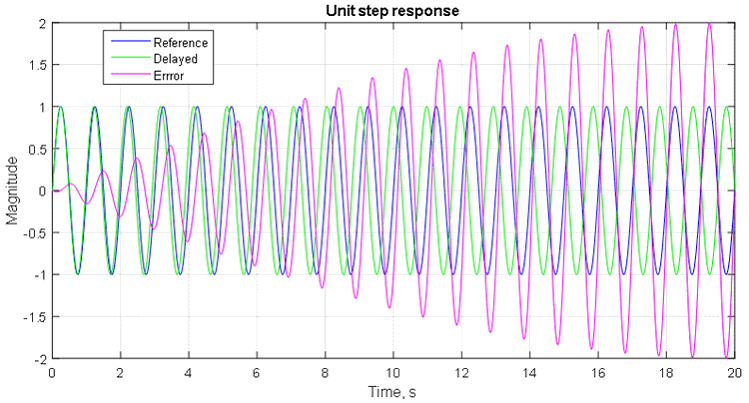
Рис. 12. Зависимость рассогласования (ошибки) от фазы между двух синусоидальных сигналов.
В случае прохождения гармоники по контуру с коэффициентом усиления больше единицы и отрицательной обратной связью запаздывание может изменить знак обратной связи на положительный и привести к неустойчивому процессу. Отдельные гармоники могут стать причиной неустойчивого процесса.
Важно, при исследовании системы на устойчивость воздействовать на неё сигналами в спектре которых содержаться гармоники, которые лежат в полосе пропускания (усиления контура больше чем на единицу) системы.
Передаточная функция звена чистого запаздывания ![]() . Запаздывание
. Запаздывание ![]() не изменяет амплитудную характеристику системы, однако добавляет фазу пропорционально частоте, например, как показано на Рис. 13 для запаздывания 0.314 сек. В этом примере фаза достигает критического предела –pi или -180 град на частоте 10 рад/c (или 1.6 Гц).
не изменяет амплитудную характеристику системы, однако добавляет фазу пропорционально частоте, например, как показано на Рис. 13 для запаздывания 0.314 сек. В этом примере фаза достигает критического предела –pi или -180 град на частоте 10 рад/c (или 1.6 Гц).
Запаздывание, в сравнении с периодом сигнала, имеет меньшую величину для низкочастотного сигнала. Отрицательное влияние запаздывания на устойчивость системы существенно возрастает с увеличением полосы пропускания системы.
Оценить критическую величину запаздывания можно путем сравнения величины запаздывания, периода сигнала на частоте среза системы и запаса по фазе.
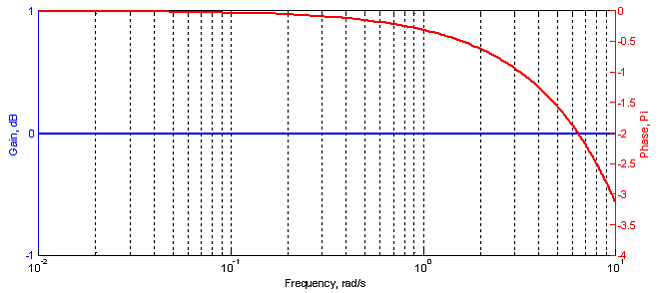
Запаздывание может быть вызвано задержкой реакции, прохождением сигнала, передачей данных, вычислением и др. процессами в контуре управления.
Неустойчивость петлевых вычислений
Во многих пособиях и учебниках, объясняющих действие обратной связи, приводится пример, показанный на Рис. 14.
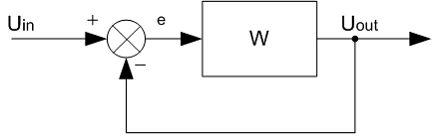
Рис. 14. Простейшая замкнутая система (система с обратной связью).
Найдем реакцию Uout на входное воздействие Uin. Для этого установим зависимость выхода от входа (входов) для каждого узла системы:.gif) откуда
откуда ![]() .Предположим, W = 2, тогда
.Предположим, W = 2, тогда ![]() . Uout = 0 при Uin = 0 и Uout = 2/3 когда Uin = 1.
. Uout = 0 при Uin = 0 и Uout = 2/3 когда Uin = 1.
Рассмотрим реакцию Uout на единичное воздействие (с момента изменения Uin от нуля до 1). Начальное значение Uout равно нулю. Результат вычислений Uout показан в таблице:
| Шаг | Uin | e= Uout-Uin | Uout = e*2 |
| 1 | 0 | 0 | 0 |
| 2 | 1 | 1 | 2 |
| 3 | 1 | -1 | -2 |
| 4 | 1 | 3 | 6 |
| 5 | 1 | -5 | -10 |
| 6 | 1 | 11 | 22 |
| 7 | 1 | -23 | -46 |
Как видно из таблицы и Рис. 15, реакция системы Uout на единичное ступенчатое воздействие Uin имеет вид расходящегося процесса. Расходящийся процесс свидетельствует о неустойчивости системы.
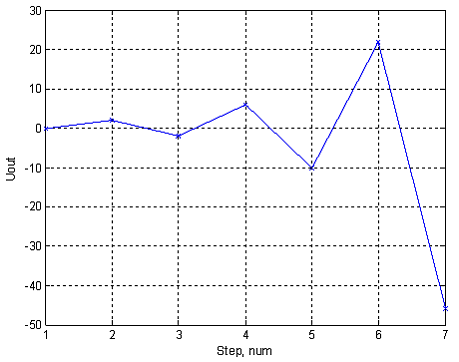
Рис. 15. Расходящийся процесс (по данным табличных вычислений).
Почему “табличная” расходящаяся реакция Uout не совпадает со значением 2/3, как это было вычислено ранее через отношение ![]() , при W = 2. В чем причина разных результатов вычисления реакции одной и той же системы на одно и тоже воздействие?
, при W = 2. В чем причина разных результатов вычисления реакции одной и той же системы на одно и тоже воздействие?
Причиной “табличной” неустойчивости является замкнутая последовательность вычислений с бесконечной полосой пропускания. Любая последовательность имеет дискретный характер, а значит, и задержку отличную от нуля фаза которой обязательно превысит предел 180 градусов в бесконечной полосе пропускания, что соответствует характеристике неустойчивого процесса. Устойчивость вычислений “аналитической” формы ![]() обеспечена одновременным (без запаздывания) вычислением результата.
обеспечена одновременным (без запаздывания) вычислением результата.
Для обеспечения устойчивости петлевых вычислений необходимо ограничить полосу пропускания, например, введением в контур фильтра низких частот, например, апериодического звена.
Средства реализации функций управления
Передаточные функции можно реализовать самыми разными средствами: механическими, электронными, программными, и др. Ряд задач требует определенных средств, например, преобразователей электрической энергии в механическую (электро-, гидро-, пьезо-, и др. двигатели) и они не могут быть заменены программными или электронными средствами, но, в общем случае, математические функции могут быть реализованными любыми средствами. Пример реализации простейшей функции ‘умножения на 2’ электронными, механическими и программными средствами показан на Рис. 16.
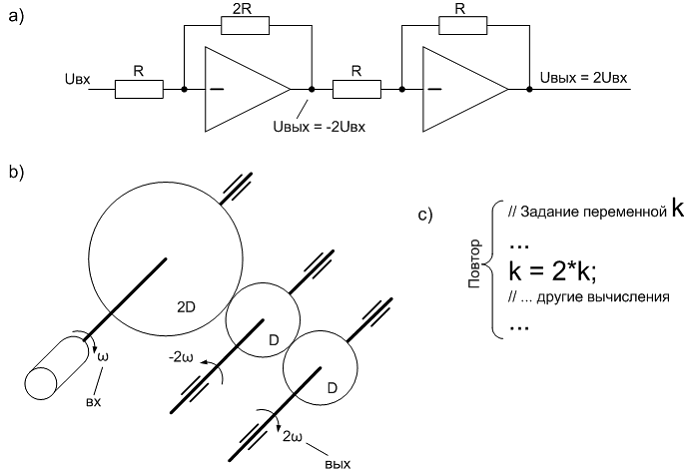
Рис. 16. Реализация операции умножения на два электронными (a, усилитель напряжения) механическими (b, редуктор) и программными (c, умножение программной переменной) средствами.
При построении системы управления необходимо оптимально распределить требуемую функцию между имеющимися средствами и необходимыми дополнительными средствами различной природы с учетом, зачастую, противоречивых требований к быстродействию, точности, устойчивости, надежности, минимизации потребляемой энергии и стоимости системы управления.
Автоматическая система на солнечной энергии без использования солнечных батарей
В этом разделе дан пример реализации авторской автоматической системы переключения потоков воды и заполнения резервуара без использования программно-электронных средств.
Система предназначена для автоматического заполнения дождевой водой бочки для нужд садового участка и отвода излишней воды от дома. Вода поступает с крыши во время дождя.
По условию пользователя в бочке не должно быть дополнительных отверстий. Система состоит из недорогих пластиковых канализационных труб и сопрягающих элементов, включая гибкое звено для уменьшения силы смещения трубы.
Принцип действия системы (Рис. 17 и Рис. 18) основан на разнице силы Архимеда (силы выталкивания) и силы тяжести. Когда бочка не заполнена, груз над бочкой m1 (лёгкая пластмассовая бутыль заполненная водой) перетягивает вертикальную трубу вместе с противовесом m2.
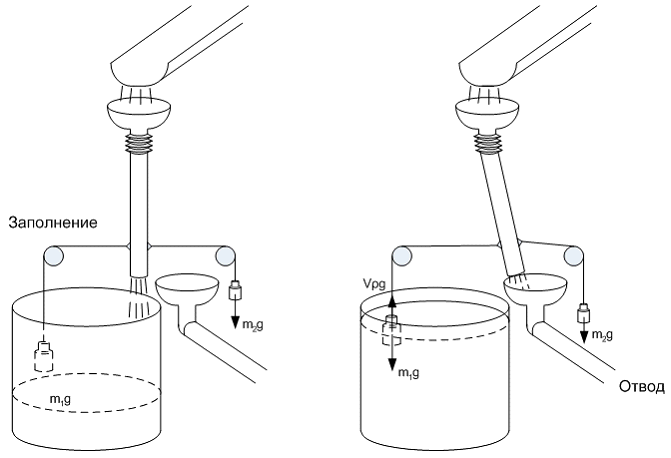
Рис. 17. Схема работы системы автоматического заполнения бочки.
По мере заполнения бочки (Рис. 17) и погружения груза m1 сила Архимеда уменьшает тягу груза m1 и m2, преодолевая сопротивление трения, начинает перетягивать трубу в свою сторону. В крайнем положении вся вода поступает в приемник водоотвода и по его наклонным трубам отводится от фундамента дома.
Для переключения трубы необходимо выполнение следующих условий.
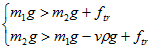 ,
,где m1 и m2 – масса бутыли и противовеса, кг; g = 9.81 – ускорение свободного падения, кг*м/c2; v – объем бутыли, литр; ![]() - плотность воды кг/литр; ftr – сила сопротивления движению трубы, Н.
- плотность воды кг/литр; ftr – сила сопротивления движению трубы, Н.
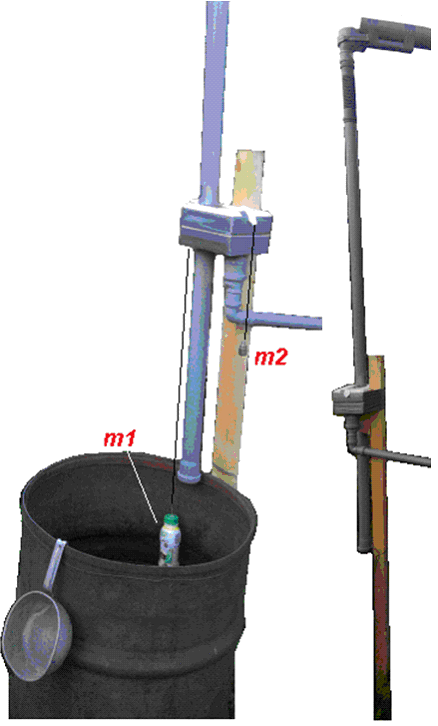
Рис. 18. Два ракурса основных компонентов автоматической системы заполнения бочки дождевой водой и отвода излишней воды.
При объеме бутыли 90 см3 (0.09 литра) и превышении веса воды бутыли, например, в пять раз больше силы трения и в 10 раз больше веса самой бутыли оптимальная масса противовеса равна 55 грамм:
Линеаризация нелинейных объектов
Аппарат анализа и синтеза линейных систем разработан достаточно хорошо, что нельзя сказать о единых подходах синтеза нелинейных систем.
Универсального метода расчета систем управления по нелинейным моделям не существует. Это объясняется большим разнообразием движений, описываемых нелинейными уравнениями и невозможностью их точного решения.
Приведение нелинейных систем к линейным позволяет значительно сократить трудозатраты на поиск оптимального решения.
Пример нелинейного объекта показан на Рис. 19. Это крышка массивного люка закрывающего вход на этаж дома. Люк имеет ость вращения и опоры для фиксации горизонтального и вертикального состояния. Момент вращения люка зависит от угла ![]() и равен произведению плеча (L) на вес (W) люка и косинус
и равен произведению плеча (L) на вес (W) люка и косинус ![]() :
:
Зависимость момента от угла для LW = 1 показана на Рис. 19. В вертикальном положении (![]() =0) момент вращения люка равен нулю и требуется малая сила, чтобы начать движение. Однако, для открывания люка, надо сначала приложить силу не меньше, чем половина его веса.
=0) момент вращения люка равен нулю и требуется малая сила, чтобы начать движение. Однако, для открывания люка, надо сначала приложить силу не меньше, чем половина его веса.
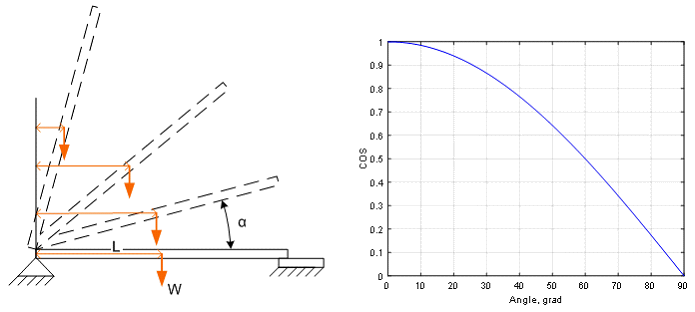
Рис. 19. Зависимость плеча L момента LW от угла поворота
Авторская схема пассивной компенсации момента сил люка противовесом с моментом M2 показана на Рис. 20 и Рис. 21 для двух положений при ![]() = 0 и 45о.
= 0 и 45о.
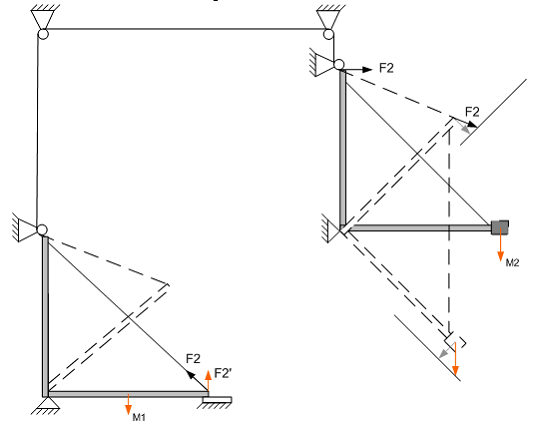
Рис. 20. Схема пассивной компенсации момента сил люка.
Программа расчета компенсации и построения результирующей силы а МатЛАБ включает следующие операторы.
a = 0:90;
L1 = 0.5; % length in m
W1 = 2; % weight in kg
M1 = W1*(L1/2)*cos(pi*a/180);
a2 = 90-(180-(90-a))/2; % angle 45..90
L2 = L1; % length in m
W2 = 1.4; % weight in kg
F2 = W2*sin(pi*a2/180); %force 1.5 .. 0
a21 = (180-a)./2; % angle 45 .. 0
F21 = F2.*sin(pi.*a21/180); % 1.5 .. 0
M2 = F21.*L2.*cos(pi.*a./180); %
figure
plot(a,M1,‘b’)
hold on
plot(a,M2,‘g’)
hold on
plot(a,M1-M2,‘m’)
grid
legend(‘M1′,‘M2′,‘total’)
xlabel(‘Angle, grad’)
ylabel(‘COS’)
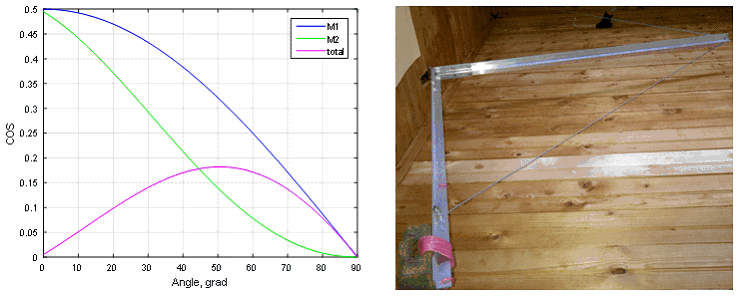
Рис. 21. Зависимость момента сил от угла поворота объекта (рисунок слева) и компоненты реального противовеса (правая фотография).
Компенсация момента люка противовесом по схеме Рис. 20 позволила уменьшить максимальный момент в 2.5 раза и свести практически к нулю начальную силу открывания люка.
При наличии места слева от оси люка для крепления ролика тросика через который подключается противовес можно применить другую схему с меньшей нелинейностью. Схема показана на Рис. 22. Оси вращения люка и противовеса совпадают. Длина троса люка и противовеса равна BC + AC = 3*141.4 см.
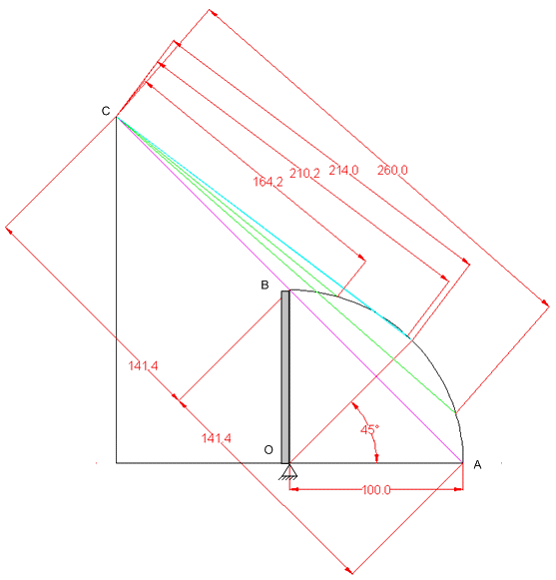
Рис. 22. Схема минимизации нелинейности открывания люка.
Зелеными и синими линиями на Рис. 22 показаны промежуточные положения точек крепления троса и углы рассогласования ACB. Нелинейность пропорциональна углу рассогласования. Угол и нелинейность уменьшаются при увеличении расстояния между точками точки C и B на линии ABC. В пределе, нелинейность равна нулю и, при отрегулированном противовесе, требуется ничтожно малая сила для перемещения люка из горизонтального положения в вертикальное.
Заключение
Поскольку объекты систем управления могут быть самой разной природы (механические, электромагнитные, биологические, химические, гравитационные, плазменные, и др. ), то помимо теории управления необходимо знать и смежные области техники, хотя бы затем, чтобы правильно сформулировать требования к проектированию отдельных узлов, которые должны выполнять свои функции в составе системы управления, а также затем, чтобы правильно оценить реализацию функций.
Иногда, казалось бы, несущественные отклонения от заданных характеристик подсистем могут заметно изменить поведение всей системы, например, люфт в механическом узле, или интерференция сигналов в электронном блоке.
Все составляющие системы (включая интерфейсы, каналы передачи данных, преобразования и фильтрации сигналов, механические узлы, и др.) должны работать на обеспечение целевых функций системы управления. Суммарное запаздывание всех элементов контура не должно превышать предельное запаздывание.
Библиографический список
- Пошехонов Л. Б. Основы теории управления. Часть 1 – линейные непрерывные системы: Учеб. пособие. СПб.: Изд-во СПбГЭТУ “ЛЭТИ”, 2006. 92 с.
- Dr. Bob Davidov. Компьютерные технологии управления в технических системах http://portalnp.ru/author/bobdavidov.
