Система Массового Обслуживания в Математическом и Имитационном моделировании

В наше время имитационное моделирование является более эффективным методом наблюдения процессов и систем различной сложности.

Имитационное математическое моделирование – это математические модели исследуемые путем решения уравнений, показывающие развитие процесса во времени при внешних воздействиях на процесс. Таковыми могут являться СМО.

Метод ИМ представляет собой построение модели, которая имитирует процесс, и расчет данных для составления отчета статистики.

Незаменимы качеством имитации является управление временем. Время в системе показывает реальное время. Также время на модели возможно пересчитать это можно сделать 2 способами:

1. Движение по времени с каким-нибудь постоянным шагом.

2. Движение от 1 события к другому, при этом изменений во времени между событиями не происходит.

Исследуем системы массового обслуживания

Данные системы бывают одноканальные и многоканальные.

В этих системах заказы обычно поступают не часто, а случайным потоком заказов. Обслуживание заказчиков длится некоторое случайное время. Потоки заказов и длительность обслуживания которые формируются случайно приводят к тому что система загружается скачкообразно: в какое-то время получается очень много заказов (или заказчики встают в очередь, или уходят необслуженными), в другое время она простаивает.

Этими системами могут быть Супермаркеты, многофункциональные центры, кафе, кассы в кино, почта И. Т. Д.

Задачей данной системы служит: время обслуживания ожидающих заказчиков, отказ в обслуживании, среднее число заявок и.т. д.

Эти системы делят на 3 типа: Система с отказами, с ожиданием, смешанного типа. Система с отказами все каналы являются заняты, заказчик уходит. Ожидание, все каналы заняты но, заказчик не уходит а становится в очередь пока один из каналов не будет свободным. Система смешанного типа все каналы являются заняты, заказчик становится в очередь, и ожидает когда его обслужат в течении ограниченного времени.

Система массового обслуживания – услуги логистики, касса приема посылок с одним менеджером по продажам и неограниченной очередью. Компания предлагает услуги доставки в Челябинск и Екатеринбург.

Клиентов, желающих купить услуги доставки в Челябинск, в среднем приходит 3 за 15 минут, в Екатеринбург 2 за 15 минут. Поток клиентов простой. Менеджер в среднем обслуживает 3 клиентов за 8 минут. Время обслуживания – показательное. Посчитать финальные вероятности P0, P1, P2, P3, среднее число заявок в СМО и в очереди, среднее время пребывания заявки в системе, среднее время пребывания заявки в очереди.

Решим поставленную задачу. Есть СМО с одним каналом и неограниченной очередью. Частичность потока входящих заявок получаем (2+3=5 клиентов за 15 минут) = (10 пассажиров в час), получаем что 

Частичность потока обслуживания получаем (3 клиента за 8 минут) = (18 клиентов за час), получаем что

Рассчитаем нагрузку СМО

нагрузка на один канал такая же:

делаем вывод что предельный режим работы системы существует.

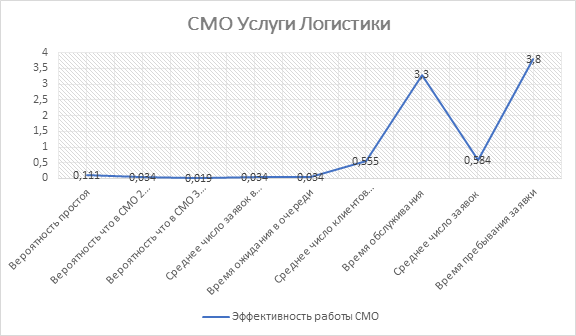
Посчитаем эффективность работы системы массового обслуживания в предельном режиме.

Вычислим конечные вероятности:

Вероятность простоя СМО:

Предположим что в системе одна заявка

Вероятность, что в системе обслуживания 2 заявки (1 клиент у менеджера и 1 клиент в очереди):

Вероятность что в системе обслуживания 3 заявки (1 клиент у менеджера и 2 клиент в очереди):

Среднее число заявок, находящихся в очереди:

Среднее время ожидания в очереди:

Среднее число клиентов покупающих услуги доставки:

Среднее время обслуживания равно:

Среднее число заявок в системе массового обслуживания:

Время пребывания заявки в СМО:

Рассмотрим модель СМО пункта выдачи транспортной компании созданную в среде  имитационного моделирования Arena.

Важным показателем логистических услуг является быстрая и бережная доставка грузов без повреждений, скорость качества обслуживания.

Рассмотрим задачу: Пункт выдачи транспортной компании хочет улучшить качество обслуживания. Самое большое кол-во заказчиков наблюдается с 17:00-18:30, когда заказчиков 6, 7, 8, 9 человек с вероятностями 0,5; 0,3; 0,1 и 0,1. Промежутки времени между прибытиями заказчиков распределены экспоненциально со средним значением 60 с. С самого начала заказчики в системе отсутствуют. Прогон модели должен соответствовать 1:30 c. Работы системы. Заказчики выбирают сами для себя 1 из 3 путей по транспортной компании.

Отдел большегрузов, касса1,2,3;

Отдел писем, посылок, касса1,2,3;

Отдел посылок, касса1,2,3.

Вероятность выбора таких путей равна 0,90; 0,20 и 0,10

На выдаче большегрузов заказчиков обслуживают по одному. В отделе выдачи посылок организовано самообслуживание обычно там очереди не бывает. В системе присутствует три кассы, у каждой из которых своя очередь.

Построение модели СМО:

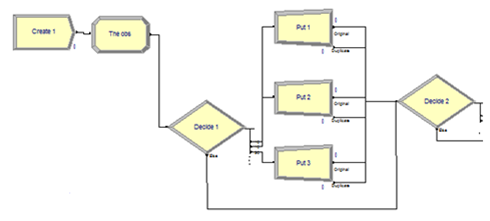
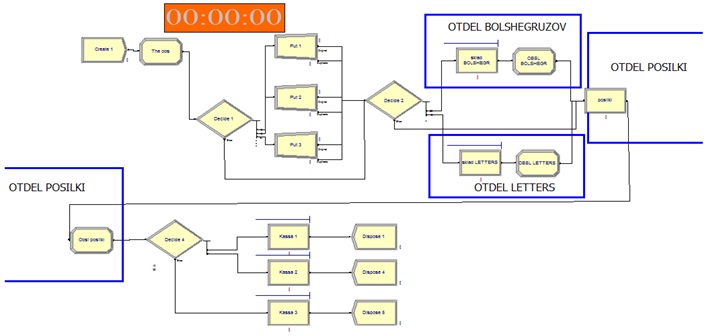
Вставляем на поле моделирования CLOCK(Время)(Рисунок 1)

Далее строим блоки Create, obs, decide, (Put1, 2, 3. Путь прохождения клиентов)(Рисунок 2).

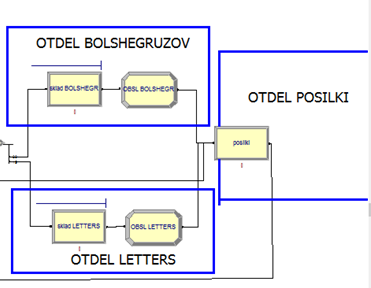
Далее на модель ставим сами отделы отдел большегрузов, отдел посылок, отдел писем(Рисунок 3).

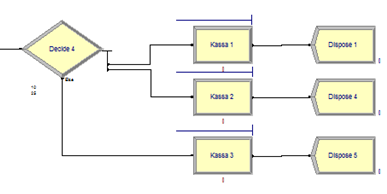
После Вставки на модель, Отделов ставим блок decide и блоки КАСС и Выход(Рисунок 4).

В результате построения блоков мы получили модель СМО пункта выдачи Транспортной компании(Рисунок 5).

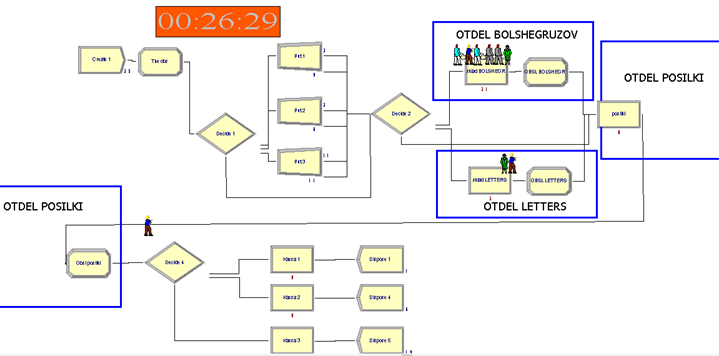
После выполнения всех пунктов построения модели, запускаем(Рисунок 6) её в результате мы видим что каждый клиент выбирает себе из трех путей какой-либо после этого клиент идет на склад писем или большегрузов в очередь, далее на выдачу, после выдачи клиент идет на кассу для оплаты если посылка, письмо, большегруз отправлен клиенту с оплатой в пункте выдачи, или просто проходит через кассу к выходу если посылка, письмо, большегруз уже оплачен клиент просто покидает пункт выдачи.

В итоге можно сделать вывод что с помощью СМО в математическом и имитационном моделировании, можно увидеть как происходит процесс обслуживания клиентов.

1. Гусева Е.Н. Имитационное моделирование экономических процессов в среде «Arena»: учеб. пособие: [электронный ресурс]. М.: Флинта, 2011. – 132 с. – Режим доступа: http://www.knigafund.ru/books/114189
2. Гусева Е.Н. Моделирование макроэкономических процессов: учеб. пособ.: [электронный ресурс]/ Е. Н. Гусева. – М.: Флинта, 2014.–214с.– Режим доступа:http://www.ozon.ru/context/detail/id/28975354/
3. Гусева Е.Н., Варфоломеева Т.Н. Применение имитационных моделей для решения экономических задач оптимизации/Гусева Е.Н., Т.Н. Варфоломеева //Современные проблемы науки и образования. 2014. № 6. С. 200.
4. Гусева Е.Н. Имитационное моделирование социально-экономических процессов. – Магнитогорск: изд-во Магнитогорск. гос. техн. ун-та им. Г.И. Носова, 2015. – 25с.
5. Гусева Е.Н. Основы имитационного моделирования экономических процессов: лаб. практикум / Е.Н. Гусева. – Магнитогорск: МаГУ, 2008. – 100с.
6. Гусева Е.Н. Имитационное моделирование социально-экономических процессов. – Магнитогорск: изд-во Магнитогорск. гос. техн. ун-та им. Г.И. Носова, 2015. – 25с.
7. Курзаева Л.В. Введение в теорию систем и системный анализ: учеб.пособие/Л.В. Курзаева. -Магнитогорск: МаГУ, 2015. -211 с.
8. Курзаева Л.В. Дистанционный курс «Инструментальные методы поддержки принятия решений»: электронный учебно-методический комплекс//Хроники объединенного фонда электронных ресурсов Наука и образование. 2016. -№ 1 (80). -С. 2.
9. Курзаева Л.В. Дистанционный курс «Основы математической обработки информации»: электронный учебно-методический комплекс//Хроники объединенного фонда электронных ресурсов «Наука и образование». -2014. -Т. 1, № 12 (67). -С. 117.
10. Курзаева Л.В. Использование имитационного моделирования как метода исследования логистики /Л.В. Курзаева// Научные труды SWorld. -  2006. – Т. 2. – № 1. – С.

Все статьи автора «Мизинов Александр Алексеевич»