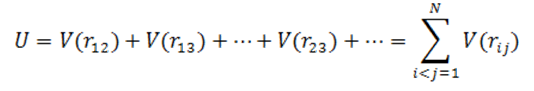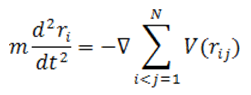Реальные физические системы состоят из огромного числа взаимодействующих между собой частиц. Как решить задачу об описании поведения этой сложной многочастичной системы? Наиболее очевидный подход к решению данной задачи – прямое решение микроскопических уравнений движения частиц (применение метода молекулярной динамики – МД). При этом наибольший интерес представляют не сами траектории, а вычисляемые с их использованием характеристики изучаемых систем, например, термодинамические характеристики, вычисляемые усреднением по траекториям.
С целью понимания качественных свойств данных систем, предположим, что движение молекул является классическим, а сами молекулы – химически инертны. Так же условимся, что сила взаимного воздействия двух молекул друг на друга, будет зависеть от расстояния между ними. Полная потенциальная энергия U будет определяться суммой двух частичных взаимодействий:
где V(rij) зависит только от абсолютной величины rijмежду частицами i и j. При использовании модели двух частичного взаимодействия, описание поведения статистической системы сводится к выбору вида потенциала V(r) и решению задачи Коши сиcтемы дифференциальных уравнений
Одной из наиболее употребительных формул для описания потенциала межмолекулярного взаимодействия является формула потенциала Лейнарда-Джонсона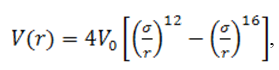
где σ – «характерная» длина потенциала, а V0 – глубина потенциальной ямы. После этапа составления математической модели, необходимо выбрать алгоритм решения. Контролировать устойчивость численного решения можно путем наблюдения за полной энергией системы, величина которой в идеальном случае должна оставаться постоянной. Для этих целей подходит скоростная форма алгоритма Верле [1].
При использовании метода МД для моделирования поведения газов и жидкостей предполагается, что система находится в некоторой кубической ячейке – МД-ячейке. Будем считать, что МД-ячейка имеет линейный размер L, ее объем V=L3. Для уменьшения вклада при отражении частицы от стенок ячейки введем периодические граничные условия для наблюдаемой величины A:
где n = (n 1,n 2,n 3) , а n1, n2, n3 – произвольные целые числа.
Этот алгоритм содержит следующую последовательность действий: после того, как частица пересечет грань основной ячейки, она возвратится в ячейку через противоположную грань с такой же скоростью. Путем введения периодических граничных условий нейтрализуется влияние граней и вводится квазибесконечный объем для увеличения точности описания макроскопической системы, т.е. МД-ячейка оказывается «встроенной» в среду.
Данная статистическая система является детерминированной, так как для описания ее поведения решается задача Коши системы линейных дифференциальных уравнений с постоянными коэффициентами. При этом получаемые решения зависят от начальных условий ri(0), υi(0) (начальной конфигурации системы). Одним из возможных вариантов задания начальных условий – размещений частиц в узлах некоторой прямоугольной сетки (размер которой должен быть меньше размера МД-ячейки) и задания векторов их скоростей случайным образом с помощью генератора случайных чисел, использующим равномерный закон распределения.
Данная задача была решена в программной среде Matlab [2]. Для ее реализации были созданы m-файлы, содержащие описания: 1) функции, возвращающей начальную конфигурацию системы; 2) функции, возвращающей мгновенные ускорения каждой частицы системы и мгновенное значение потенциальной энергии; 3) функции, возвращающей значения координат, составляющей скорости и ускорения вдоль соответствующих координат осей; 4) функции, возвращающей составной массив, содержащий значения координат, проекций скоростей и ускорений на соответствующие координатные оси в узлах временной сетки.
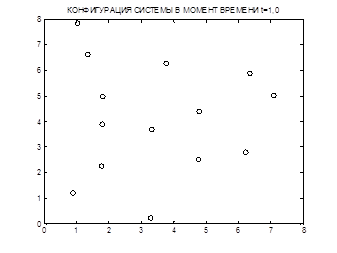
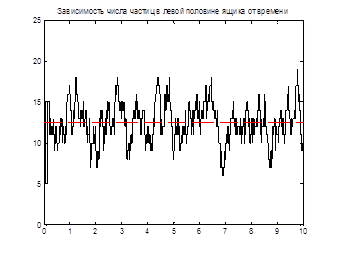
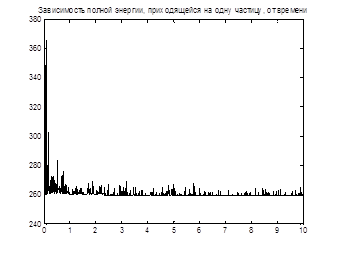
Компьютерное моделирование было проведено с числом частиц N=25, 36 и 49, и размером ячейки 8, 10, 20 (в отн. ед). Анализ зависимостей, представленных на рисунках1-4, показывает, что с течением времени система стремится к состоянию равновесия (процесс релаксации), в котором примерно одинаковым остаются число частиц в левой и правой половинах МД-ячейки и полная энергия системы.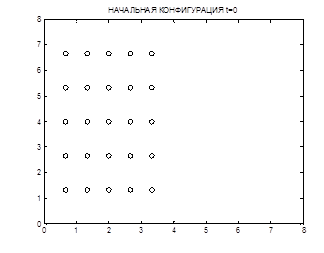
Рис 1. Начальная конфигурация t=0
Рис 2. Конфигурация системы в момент времени t=1
Рис 3. Зависимость числа частиц в левой половине ящика от времени
Рис 4. Зависимость полной энергии, приходящейся на одну частицу, от времени
Библиографический список
- Хеерман Д.В. Методы компьютерного эксперимента в теоретической физике. М.: Мир, 1990.
- Дьяконов В. П. MATLAB. Полный самоучитель. – М.: ДМК Пресс, 2012. – 768 с.: ил.