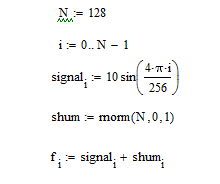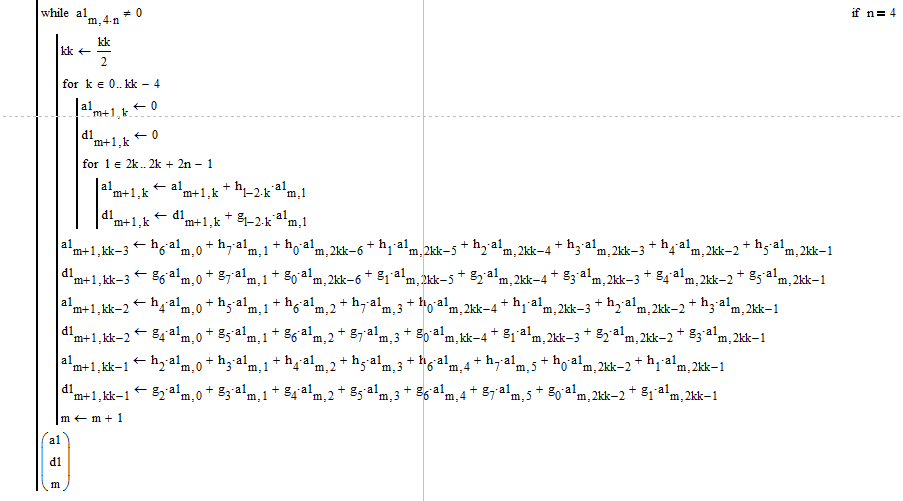Вейвлет-преобразование является новым этапом развития преобразования Фурье, которое используется для разложения функций в ряды. Вейвлеты появились для разложения нестационарных функций. Существуют самые разнообразные вейвлеты, которые применяются для решения различных задач: обработка экспериментальных данных, обработка изображений, удаление шума (фильтрация), сжатие данных, сжатие файлов с изображением, реставрация и идентификация изображений. Вейвлет-разложение очень трудоемко, поэтому появилось быстрое вейвлет-преобразование.
Данная статья посвящена реализации алгоритма прямого вейвлет-преобразования, приведенного, например в работах [1-2], средствами пакета MathCad.
Сначала задано количество реализаций сигнала N и реализован “зашумленный” сигнал f, как показано на рисунке 1 .
Рис.1. Задание исходного сигнала.
Затем задан порядок фильтра n. Так как были выбраны вейвлеты Добеши, в функции Dobesh_hg(n), присваиваются коэффициенты h и g, в зависимости от порядка фильтра n. Далее, для ускорения расчетов при прямом вейвлет-преобразовании, коэффициенты делятся на √2. Это реализовано в MathCad, как показано на рисунке 2.
Рис.2. Задание коэффициентов Добеши.
Затем в нулевую строку матрицы a1 заносим сигнал f, переменной kk, в которой хранится количество столбцов, присваиваем значение N, уровню m присваиваем значение 0.
Для случая n=2, пока элемент столбца 4n не равен нулю (это определяет наименьший размер сигнала, который можно восстановить), в цикле уменьшаем количество столбцов в два раза, в цикле по k находим коэффициенты аппроксимирующего сигнала a1 и детализирующего сигнала d1 (от 0 до kk-2 столбца) этого уровня разложения, в двух циклах по l находим последние элементы и увеличиваем номер уровня разложения. Реализация в MathCad приведена на рисунке 3.
Рис.3. Разложение сигнала при порядке вейвлета Добеши n=2.
Если же n=4, аналогично в цикле уменьшаем количество столбцов, в цикле по k находим элементы от 0 до kk-4 столбца, затем находим последние три элемента и увеличиваем номер уровня разложения.
Возвращаются из функции коэффициенты a1,d1 и номер максимального уровня разложения m.
Рис.4. Разложение сигнала при порядке вейвлета Добеши n=4.
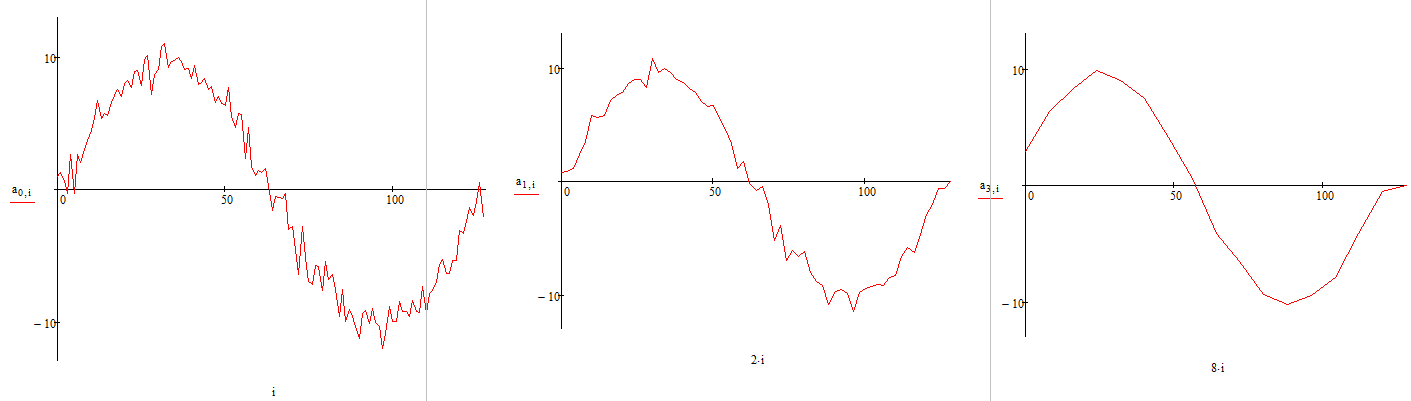
Разложения на более высоких уровнях получается более сглаженными, то есть сигнал фильтруется от шумов.
а) исходный сигнал б) разложение на уровне 1 в) разложение на уровне 3
Рис.5. Разложение исходного сигнала на различных уровнях
К достоинствам данного алгоритма относится экономия памяти, так как нт необходимости хранить для вейвлет-преобразования всю разреженную матрицу, как это предлагается в [2] . А также достоинством является решение задачи стандартными средствами MathCad, без использования расширения Wavelet Extension Pack этого пакета, предназначенного для работы с вейвлетами.
Библиографический список
- Воскобойников Ю. Е. Фильтрации сигналов и изображений: Фурье и Вейвлет алгоритмы (с примерами в Mathcad) : монография / Ю. Е. Воскобойников, А. В. Гочаков, А. Б. Колкер ; Новосиб. гос. архитектур.-строит. ун-т (Сибстрин).– Новосибирск : НГАСУ (Сибстрин), 2010. – 188 с.
- Иванов М.А. Применение вейвлет-преобразований в кодировании изображений / М.А. Иванов // Новые информационные технологии в науке и образовании. — 2004. — № 24. — С. 157–175.