Введение.

Литий-ионные аккумуляторы являются стандартом де-факто в области источников питания для электромобилей, систем бесперебойного питания, мобильных устройств и гаджетов [1]. Другой пример использования литий-ионных аккумуляторов – накопители для возобновляемых источников энергии (главным образом, солнечные батареи и ветрогенераторы). Так в 2011 году в Китае был установлен накопитель на литий-ионных аккумуляторах общей емкостью 36 МВтч, способный отдавать в сеть 6 МВт электрической мощности в течение 6 часов [2]. Примером противоположного масштаба являются литий-ионные батарей для имплантируемых кардиостимуляторов, ток нагрузки которых составляет порядка 10 мкА [1]. Сам диапазон емкости единичного коммерчески выпускаемого литий-ионного элемента давно перешагнул отметку 500 Ач [3].

Использование литий-ионных аккумуляторов предполагает соблюдение параметров разряда и заряда батареи, в противном случае может произойти необратимая деградация емкости, выход из строя и даже возгорание батареи из-за саморазогрева. Поэтому литий-ионные аккумуляторы всегда применяются вместе с системой контроля и управления – СКУ или BMS (battery management system) [4]. Система управления батареей выполняет защитные функции, контролируя температуру, ток заряда-разряда и напряжение, таким образом предотвращая слишком глубокий разряд, перезаряд и перегрев. Также BMS осуществляет контроль состояния батареи с помощью оценки степени заряда (State of Charge, SOC) и состояния годности (State of Health, SOH). Интеллектуальный BMS является необходимым в практически любом применении литий-ионных батарей, предоставляя информацию сколько устройство будет работать до необходимости подзарядки (значение SOC) и когда следует заменить батарею из-за потери емкости (значение SOH).

В настоящей работе мы сосредоточимся на моделях для оценки состояния SOC и SOH, пригодных для реализации в реальном времени в системах управления батареями. К сожалению, в русскоязычной научной литературе практически отсутствуют какие-либо публикации, рассматривающие подобные вопросы именно для литий-ионных аккумуляторов. Поэтому в этой статье мы попробуем восполнить данный пробел.

1. Предварительные сведения.

1.1. Литий-ионная батарея – элементарное описание.

Схематически процессы разряда и заряда литий-ионного аккумулятора можно представить на рисунке 1 [5].

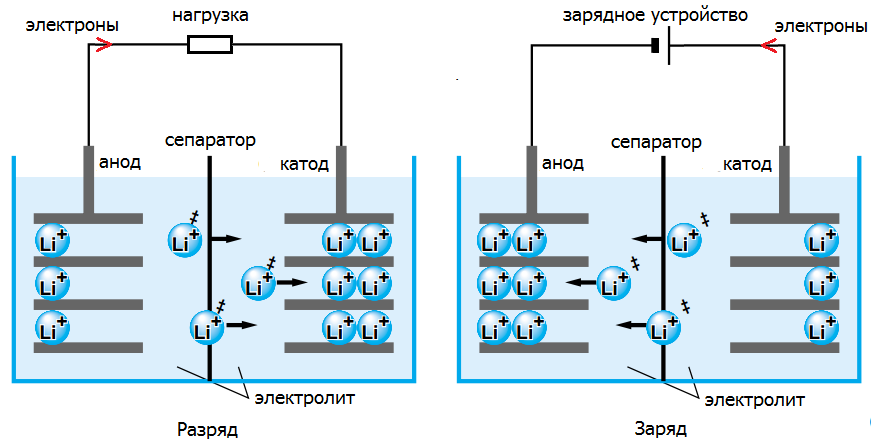
Рисунок 1. Элементарное представление процессов в литий-ионном аккумуляторе.

Батарея состоит из углеродного анода и катода из оксида металла, содержащего также литий (например, LiMn2O4). Положительные ионы лития Li+ мигрируют между анодом и катодом через органический электролит. Важным моментом является то, что литий никогда не возникает в свободном металлическом состоянии – происходит только обмен его ионами между катодом и анодом. Поэтому такие аккумуляторы получили название «литий-ионные»

При заряде литий-ионного аккумулятора происходит деинтеркаляция (изъятие) лития из литийсодержащего катода и интеркаляция (внедрение) ионов лития в углеродный материал анода. При разряде аккумулятора процессы идут в обратном направлении: отрицательный заряд переносится потоком электронов с катода на анод, а ионы лития двигаются в обратном направлении – с анода на катод.

Более подробное описание процессов мы рассмотрим при моделировании аккумулятора на электрохимическом уровне.

1.2. Системный уровень описания батареи.

Со схемной точки зрения, батарея представляется двухполюсником. В данной работе будет использоваться ее описание в виде черного ящика, как системы с одним входом (ток в цепи ) и напряжение на клеммах батареи .

Напряжение холостого хода (open circuit voltage, OCV) – напряжение на клеммах батареи при отсутствии отбора тока .

Важнейшим параметром является емкость батареи , определяемая как максимальное количество электрической энергии (в Ач), которое батарея отдает в нагрузку с момента полного заряда до состояния разряда, не приводящего к преждевременной деградации батареи.

Как было сказано ранее, основные функции интеллектуального BMS – это оценка SOC и SOH.

Состояние заряда батареи (state of charge, SOC) – показатель, характеризующий степень заряженности батареи: 100% – полный заряд, 0% – полный разряд. Эквивалентный показатель глубина разряда (deepth of discharge, DoD) – . Обычно SOC измеряется в процентах, но в настоящей работе мы будем считать, что . Формально, SOC выражается как , где – текущий заряд в батареи.

Состояние годности батареи (state of health, SOH) – качественный показатель, характеризующий текущую степень деградации емкости батареи. Результатом оценки SOH является не численное значение, а ответ на вопрос: «необходимо ли заменить батарею в данный момент?». В настоящее время нет стандарта, регламентирующего на основе каких параметров батареи должен вычисляться SOH. Разные производители BMS используют для этого различные показатели, например, сравнение исходной и действительной емкости батареи или внутреннего сопротивления.

2. Модели для определения состояния заряда.

Определение состояния заряда SOC является задачей наблюдения за скрытым состояниям системы по имеющейся модели процесса и измеряемому выходному отклику от входного воздействия . Модели, предназначенные для использования в составе систем управления батареями для определения SOC, могут быть классифицированы на две большие группы [7]:

- эмпирические модели, реплицирующие поведение батареи с позиции «черного ящика»;

- физические модели, моделирующие внутренние электрохимические процессы в батарее.

2.1 Эмпирические модели.

Класс эмпирических моделей включает в себя ряд различных подходов, общими чертами являются существенное упрощенное моделирование физических процессов в батарее. Эмпирические модели являются стандартом при реализации BMS, поскольку обладают с одной стороны достаточной простотой для реализации, а с другой – приемлемой точностью для оценки SOC [7], [8]. Количественное сравнение 28 разных эмпирических моделей содержится в работе [23].

Основной вид эмпирических моделей – схемы замещения.

Исходной предпосылкой к эмпирическому моделированию является наблюдение, что динамика аккумуляторной батареи может быть разделена на две части [9],[10]:

- медленная динамика, связанная с зарядом и разрядом батареи,

- быстрая динамика, связанная с внутренним импедансом батареи: активным сопротивлением электролита и электродов, а также с электрохимическими емкостями.

Типичный масштаб времени: единицы-десятки часов для медленной динамики (от полного заряда до разряда), десятки минут для быстрой динамики (рассасывание носителей зарядов в паразитных емкостях и переход батареи в установившееся состояние).

Процессы старения и деградации емкости моделируются как нестационарность параметров системы.

2.1.1 Напряжение холостого хода.

Фактически, медленная динамика сводится к моделированию влияния SOC на электрические характеристики аккумулятора. Замечено, что напряжение холостого хода (OCV) является достаточно однозначной функцией от состояния заряда (SOC или DoD):

(1)

и слабо подвержено температурной вариации (кроме областей, где батарея почти полностью заряжена или разряжена), а также слабо меняется при старении батареи (если считать когда батарея заряжена до своей текущей с учетом деградации емкости) [4].

Типичные кривые зависимости для литий-ионных аккумуляторов с разной химией показаны на рисунке 2.

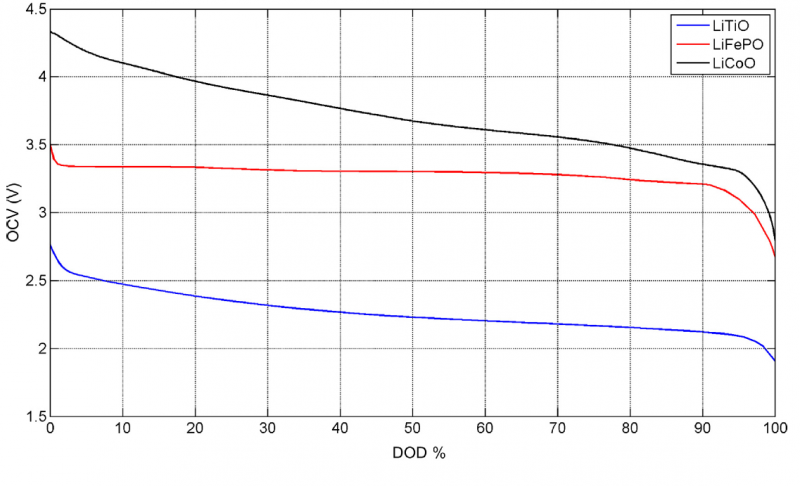
Рисунок 2. Типичные зависимости напряжения холостого хода от состояния заряда.

Аппроксимация зависимости может быть выполнена различными способами, в том числе кусочно-линейно или полиномиально. Одним из классических вариантов аппроксимации (1) является уравнение Шеферда (Shepherd model) [11], модификация которого для литий-ионного аккумулятора имеет вид [12]:

где коэффициенты вычисляются на основе характерных точек кривой разряда батареи, которая обычно приводится в технической документации, а – полный заряд, прошедший из или в батарею за время : .

В работе [9], например, используется следующее выражение для аппроксимации :

Различные варианты параметризации систематически рассмотрены в работе [14].

Для получения полной модели батареи уравнение (2) может быть дополнено также слагаемыми, зависящими от тока батареи, например как это реализовано в системе Simulink в блоке Battery из SimPowerSystem ([12], [13]).

2.1.2 Внутренний импеданс батареи.

Вторая часть эмпирической модели – описание внутреннего импеданса, отвечающего за вольт-амперные характеристики и быструю динамику.

Самым простым вариантом моделирование является включенное последовательно с регулируемым источником ЭДС активное сопротивление (рисунок 3). Такая схема замещения моделирует внутреннее сопротивление батареи, создаваемое материалами электродов и электролита, на котором наблюдается омическое падение напряжения и выделение тепла.

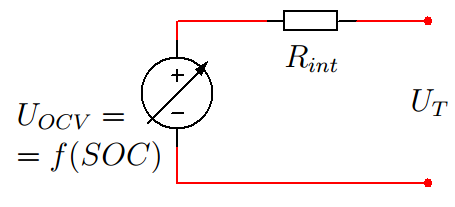
Рисунок 3. Элементарная схема замещения батареи.

Для моделирования переходных процессов в батарее такая простейшая схема замещения должна быть дополнена реактивными элементами. Таким образом, последовательно с оказывается включено комплексное сопротивление с импедансом .

Обычно выделяют следующие электрохимические явления, существенно влияющие на динамику электрических переходных процессов ([8], [15]):

- классический двойной электрический слой в контакте электрод-электролит (Double-Layer)

- образование пассивной плёнки (solid-electrolyte interface, SEI) на электродах.

В результате этих факторов, внутри литий-ионного аккумулятора возникают электрохимические распределенные конденсаторы. Исследование импеданса батареи осуществляется с помощью электрохимической импедансной спектроскопии (Electrochemical Impedance Spectroscopy, EIS) [16]-[17].

Предложено достаточно большое количество эквивалентных схем [18]-[19], начиная от простых, содержащих несколько реактивных элементов, заканчивая детальным моделированием электрохимических явлений с помощью большого числа RC-цепочек [20], и даже нелинейных элементов [21].

Практически хорошо зарекомендовавший вариант (рисунок 4) эквивалентной схемы основан на последовательном соединении активного внутреннего сопротивления и двух RC-цепочек, моделирующих процессы поляризации с образованием объемных емкостей:

- электрохимическая емкость двойного слоя , влияние которой наблюдается на более высоких частотах,

- емкость , связанная с интеркаляцией и массообменом лития, доминирующая на низких частотах.

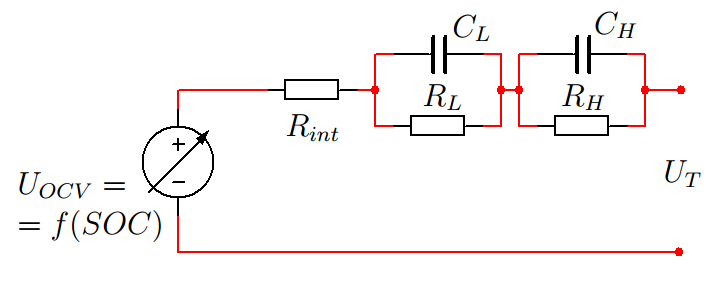
Рисунок 4. Схема замещения для динамической модели батареи второго порядка.

Таким образом, представленная на рисунке 4 динамическая модель второго порядка в пространстве состояний записывается в виде:

(3)

где , а параметры подбираются на основе экспериментальных данных, снятых с конкретного типа батареи.

В действительности, импеданс батареи является функцией от температуры и SOC, а в долгосрочном масштабе времени – также меняется при старении батареи.

Внутреннее активное сопротивление уменьшается при повышении температуры, но в пределах диапазона 25-40°C, оно остается достаточно стабильным [22]. Эксперименты, проведенные в [9] с полимерными литий-ионными аккумуляторами, показали, что параметры схемы замещения остаются постоянным при SOC больше 20%. При меньших значениях SOC происходит экспоненциальное увеличение сопротивлений и экспоненциальное уменьшение емкостей .

2.1.3 Моделирование состояния заряда.

Поскольку величина SOC изменяется в процессе заряда и разряда батареи, то естественно рассматривать SOC как еще одно состояние системы, добавив в схему замещения фрагмент для его моделирования.

Полная схема замещения представлена на рисунке 5. В схему добавлена изолированная цепь с управляемым источником током, обеспечивающим ток через и , равный току в цепи батареи . Таким образом осуществляется разряд и заряд емкости , моделирующей емкость батареи. Напряжение на емкости численно равно SOC, . Значение емкости определяется следующим образом [9]:

где – полная емкость аккумулятора в Ач, – корректирующий множитель для учета зависимости емкости батареи от температуры , – корректирующий множитель для моделирования процесса старения ( – число циклов заряда-разряда).

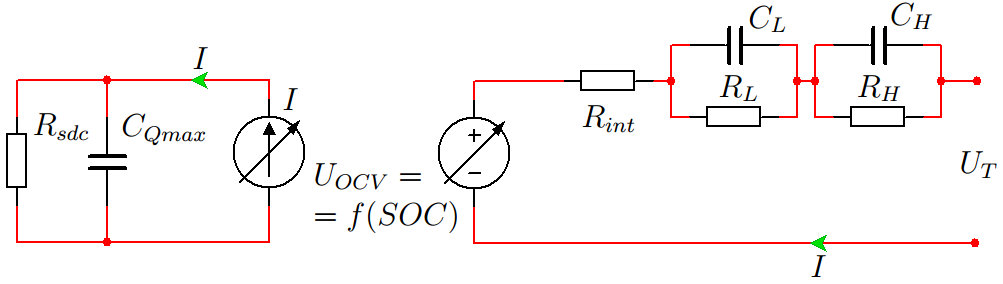
Рисунок 5. Полная схема замещения для динамической модели второго порядка.

Сопротивление моделирует саморазряд батареи.

С учетом введенного фрагмента схемы, модель батареи в пространстве состояний дополняется еще одним уравнением для переменной :

(4)

Собственно задача определения SOC сводится к синтезу наблюдателя для модели (3)-(4).

2.2 Физические модели.

Некоторые исследователи предлагают использовать физические модели для предсказания SOC и SOH. Данный класс моделей основан на использовании уравнений, описывающих электрохимические процессы в батарее.
Главное преимущество такого подхода достаточно очевидно – достигается высокая точность моделирования за счет перехода с эмпирического на физический уровень описания модели. Недостатками являются высокая вычислительная сложность модели и большое количество параметров, подлежащих идентификации из экспериментальных данных. Несмотря на это, физические модели представляют достаточный интерес для будущих поколений систем управления батареями.

В литературе представлены два класса физических моделей:

- одночастичная модель (single particle model) [24]-[27],

- одномерная пространственная модель (1D-spatial model) [28].

Одночастичная модель основана на допущении, что каждый из электродов литий-ионного элемента может рассматриваться как одна сферическая частица достаточно большого радиуса (чтобы ее площадь поверхности соответствовала площади пористого катода или анода батареи). Изменение концентрации и потенциала в электролите игнорируется, как и температурные эффекты.

Одномерная пространственная модель является дальнейшим развитием одночастичной модели, в которой каждый из электродов моделируется в виде множества пересекающихся сфер с центрами на одной линии. Такой подход позволяет более точно описать процесс интеркаляции (диффузии) ионов лития в пористые электроды батареи.

Заметим, что даже такие приближенные физические модели литий-ионных батарей основаны на уравнениях в частных производных и синтез наблюдателей для подобного рода объектов представляет собой отдельную нетривиальную задачу.

2.2.1 Одночастичная модель.

Одночастичная модель основана на моделировании следующих явлений в батарее: диффузия ионов лития в электроды и электрохимическая кинетика потока ионов. Процессы в электролите (жидкой фазе) представляются в виде постоянной проводимости и фактически не моделируются. Схематическая структура батареи в одночастичной модели показана на рисунке 6. Далее мы кратко воспроизведем основные составляющие модели. Все уравнения предполагаются одинаково удовлетворяющие как условиям реакции на аноде, так и в равной степени на катоде (с соответствующими параметрами).

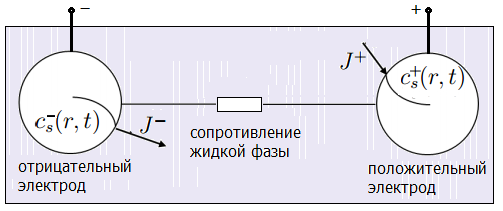
Рисунок 6. Схематическое представление аккумулятора в одночастичной модели.

Интеркаляция лития в электроды моделируется как диффузия, описываемая законом Фика:

где – концентрация ионов лития в электродах (твердой фазе), – коэффициент диффузии.

Это уравнение может быть переписано в сферических координатах

с граничными условиями

где все уравнения далее записываются отдельно для параметров анода и катода: , , – молярные потоки диффузии через поверхность электродов, – радиус электродов.

Молярные потоки диффузии могут быть выражены как плотность тока через поверхность электродов:

, (5)

где – постоянная Фарадея, – эффективная площадь поверхности каждого электрода.

Для оценки состояния заряда аккумулятора, удобно перейти от локальных концентраций к усредненным по всему объему электродов – :

Непосредственные вычисления показывают [26], что производная по времени находится как

(6)

где – коэффициент пропорциональности, – ток батареи.

Электрохимическая кинетика моделируется с помощью уравнения Батлера-Фольмера (Butler-Volmer equation) для молярного потока ионов лития:

(7)

в котором перенапряжения могут быть выражены следующим образом

(8)

где – потенциалы положительного и отрицательного электродов, – функция от концентрации ионов лития на поверхности электродов, – сопротивление электролита (жидкой фазы) и пассивной пленки на электроде, – универсальная газовая постоянная, – температура батареи.

Уравнение (7) может быть решено относительно перенапряжения с учетом, что потоки выражаются через ток батареи с помощью (5):

(9)

где – константы, выражающие плотность обменного тока.

Заметим, что напряжение на контактах батареи равно разности потенциалов , при этом потенциалы могут быть выражены через (8) с помощью подстановки (9). Отсюда, получаем искомое

(10)

Уравнения (6) и (10) составляют электрохимическую одночастичную модель литий-ионного аккумулятора.

2.2.2 Связь между одночастичной моделью и схемой замещения.

Концентрации для положительного электрода и отрицательного связаны друг с другом из уравнения (6): при увеличении , концентрация пропорционально уменьшается, и наоборот. Очевидно, что состояние заряда пропорционально концентрации . Тогда можно ввести в рассмотрение величину как состояние системы, при этом концентрации и будут линейно зависеть от : , .

Отсюда можно записать следующее уравнение для в одночастичной модели

(11)

где – некоторая положительная константа.

Слагаемое в (10), исходя из введенного состояния , от которого линейно зависят от концентрации и , может быть представлено в виде некоторой функции . В работе [29] предложена следующая аппроксимация для :

где – постоянные коэффициенты, идентифицируемые по экспериментальным данным.

Оставшаяся часть (10) представляет собой функцию от тока , для которой в [29] предложена такая параметризация:

где – постоянные коэффициенты, идентифицируемые по экспериментальным данным.

Модель в пространстве состояния окончательно получается в виде:

(12)

Сопоставляя (4) и (11), достаточно очевидно, что уравнение состояния заряда в одночастичной модели (11) полностью аналогично представлению схемой замещения (4), при этом саморазряд батареи не моделируется. Из уравнения в (12) следует, что функции соответствует функция для напряжения холостого хода в схеме замещения. Но при этом в одночастичной модели существует дополнительный нелинейный элемент с падением напряжения , включенный последовательно с внутренним активным сопротивлением . В отличие от эмпирического представления схемой замещения, электрохимическая емкость двойного электрического слоя не моделируется в одночастичной модели.

Сама электрохимическая одночастичная модель может быть представлена в виде схемы замещения, показанной на рисунке 7.

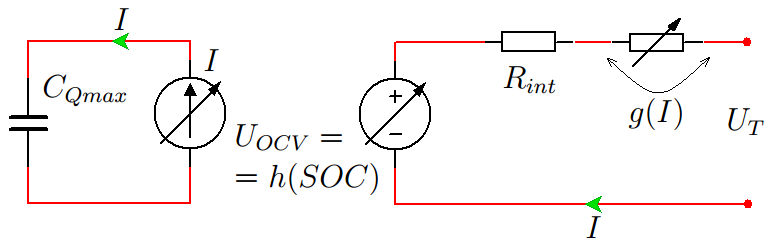
Рисунок 7. Эквивалентная схема замещения для одночастичной модели.

Заключение.

В настоящей работе дан обзор двух вариантов моделей литий-ионных аккумуляторов для систем управления батареями. Показано, что эмпирическая модель на основе схемы замещения является самой распространенной в литературе, простой для реализации и гибкой с точки зрения масштабирования для моделирования специальных явлений в аккумуляторе. Параметры модели являются нестационарными, подверженными как процессу старению батареи, так и вариации от состояния заряда и температуры. На основе анализа последних публикаций сделан вывод, что перспективным направлением совершенствования моделей для нового поколения систем управления батарей является физические модели, количественно описывающие электрохимические явления в аккумуляторе. Показано, что одночастичная электрохимическая модель может быть представлена в виде схемы замещения, имеющей сходство с эмпирической моделью.

Библиографический список

1. Ramadesigan V. et al. Modeling and simulation of lithium-ion batteries from a systems engineering perspective //Journal of The Electrochemical Society. – 2012. – Т. 159. – №. 3. – С. R31-R45
2. Гаранжа A. В Китае изготовлена самая большая в мире аккумуляторная батарея [Электронный ресурс] / A. Гаранжа – Режим доступа: http://www.liotech.ru/sectornews_207_503 – Загл. с экрана.
3. Axcom Battery Technology GmbH, CNFJ-500 2V/500Ah product specification [Электронный ресурс] – Режим доступа: http://www.axcom-battery-technology.de/uploads/media/Lead_Crystal_Battery_CY2-500.pdf – Загл. с экрана
4. Pistoia G. (ed.). Lithium-Ion Batteries: Advances and Applications. – Newnes, 2013. – 634 p.
5. Lithium Ion Rechargeable Batteries: Technical Handbook, Sony Corporation [Электронный ресурс] – Режим доступа: http://www.sony.com.cn/products/ed/battery/download.pdf – Загл. с экрана.
6. Выравнивание параметров секций аккумулятора обеспечивает дополнительное время работы и увеличивает срок службы аккумуляторных батарей [Электронный ресурс] – Режим доступа: http://www.scanti.ru/bulleten.php?v=211&p=44 – Загл. с экрана
7. Rahimian S. K., Rayman S., White R. E. Comparison of single particle and equivalent circuit analog models for a lithium-ion cell //Journal of Power Sources. – 2011. – Т. 196. – №. 20. – С. 8450-8462.
8. Rahimi-Eichi H., Ojha U., Baronti F., Chow M. Battery Management System: An Overview of Its Application in the Smart Grid and Electric Vehicles // Industrial Electronics Magazine, IEEE — June 2013. — vol.7, no.2, — pp.4-16
9. Chen M., Rincon-Mora G. A. Accurate electrical battery model capable of predicting runtime and IV performance //Energy conversion, ieee transactions on. — 2006. — Т. 21. — №. 2. — С. 504-511.
10. V. Pop, H.J. Bergveld, D. Danilov, P.P.L. Regtien, P.H.L. Notten, Battery Management Systems: Accurate State-of-Charge Indication for Battery-Powered Applications. ISBN: 978-1-4020-6944-4, In: Philips Research Book Series, vol. 9, Springer, 2008. pp. 24?37.
11. Melentjev S., Lebedev D. Overview of Simplified Mathematical Models of Batteries. // 13th International Symposium “Topical problems of education in the field of electrical and power engineering”. — Doctoral school of energy and geotechnology : Parnu, Estonia, January 14-19, 2013. — pp. 231-235
12. Tremblay O., Dessaint L. A. Experimental validation of a battery dynamic model for EV applications // World Electric Vehicle Journal. — 2009. — Т. 3. — №. 1. — С. 1-10.
13. Боченин В.А., Зайченко Т.Н. Исследование и разработка модели Li-Ion аккумулятора // Научная сессия ТУСУР–2012: Материалы Всероссийской научно-технической конференции студентов, аспирантов и молодых ученых, Томск, 16–18 мая 2012 г. – Томск: В-Спектр, 2012 – Том 2. – с 174-177.
14. Weng C., Sun J., Peng H. An Open-Circuit-Voltage Model of Lithium-Ion Batteries for Effective Incremental Capacity Analysis //ASME 2013 Dynamic Systems and Control Conference. – American Society of Mechanical Engineers, 2013. DSCC2013-3979 – С. 1-8.
15. Tang X. et al. Li-ion battery parameter estimation for state of charge //American Control Conference (ACC), 2011. – IEEE, 2011. – С. 941-946.
16. Zhao J. et al. Kinetic investigation of LiCOO2 by electrochemical impedance spectroscopy (EIS) //International Journal of Electrochemical Science. – 2010. – Т. 5. – №. 4. – С. 478-488.
17. Jiang Y. et al. Modeling charge polarization voltage for large lithium-ion batteries in electric vehicles //Journal of Industrial Engineering & Management. – 2013. – Т. 6. – №. 2. – С. 686-697.
18. Rahmoun A., Biechl H. Modelling of Li-ion batteries using equivalent circuit diagrams //PRZEGLAD ELEKTROTECHNICZNY. – 2012. – Т. 88. – №. 7 B. – С. 152-156.
19. He H., Xiong R., Fan J. Evaluation of lithium-ion battery equivalent circuit models for state of charge estimation by an experimental approach //energies. – 2011. – Т. 4. – №. 4. – С. 582-598.
20. Wang C., Appleby A. J., Little F. E. Electrochemical impedance study of initial lithium ion intercalation into graphite powders //Electrochimica acta. – 2001. – Т. 46. – №. 12. – С. 1793-1813.
21. Lee J., Nam O., Cho B. H. Li-ion battery SOC estimation method based on the reduced order extended Kalman filtering //Journal of Power Sources. – 2007. – Т. 174. – №. 1. – С. 9-15.
22. Johnson V. H., Pesaran A. A., Sack T. Temperature-dependent battery models for high-power lithium-ion batteries. – City of Golden : National Renewable Energy Laboratory, 2001.
23. Hu X., Li S., Peng H. A comparative study of equivalent circuit models for Li-ion batteries //Journal of Power Sources. – 2012. – Т. 198. – С. 359-367.
24. Santhanagopalan S., White R. E. Online estimation of the state of charge of a lithium ion cell //Journal of Power Sources. – 2006. – Т. 161. – №. 2. – С. 1346-1355.
25. Rahimian S. K., Rayman S., White R. E. Comparison of single particle and equivalent circuit analog models for a lithium-ion cell //Journal of Power Sources. – 2011. – Т. 196. – №. 20. – С. 8450-8462.
26. Bartlett A. et al. Model-based state of charge estimation and observability analysis of a composite electrode lithium-ion battery //Decision and Control (CDC), 2013 IEEE 52nd Annual Conference on. – IEEE, 2013. – С. 7791-7796.
27. Moura S. J., Chaturvedi N. A., Krstic M. Adaptive Partial Differential Equation Observer for Battery State-of-Charge/State-of-Health Estimation Via an Electrochemical Model //Journal of Dynamic Systems, Measurement, and Control. – 2014. – Т. 136. – №. 1. – С. 011015.
28. Klein R. et al. State estimation of a reduced electrochemical model of a lithium-ion battery //American Control Conference (ACC), 2010. – IEEE, 2010. – С. 6618-6623.
29. Fang H. et al. Adaptive estimation of state of charge for lithium-ion batteries //American Control Conference (ACC), 2013. – IEEE, 2013. – С. 3485-3491.

---

Все статьи автора «Борисевич Алексей Валерьевич»