Благодаря своим широким функциональным возможностям, простоте, надежности и высокой жесткости кривошипно-ползунный механизм является наиболее распространенным механизмом, используемым в главных (ГИМ) и дополнительных (ДИМ) исполнительных механизмах прессов, средствах механизации. Задачи и методы синтеза и анализа этого механизма достаточно полно рассмотрены в многочисленных работах, например в работах основоположников теории механизмов [1, 2]. Тем не менее, в связи со спецификой использования его в реальных конструкциях прессов и вспомогательных устройств возникает необходимость дополнительного исследования кинематических свойств механизма.
В данной работе приведено определение основных кинематических характеристик дезаксиального механизма, необходимых для его синтеза и последующего анализа. Основное внимание уделено учету специфических особенностей использования механизма в качестве исполнительных механизмов прессов и средств механизации.
Схема дезаксиального кривошипно-ползунного механизма в текущем положении показана на рис. 1. Механизм относится к рычажному механизму II класса с одной степенью подвижности и содержит 3 подвижных звена, три вращательные и одну поступательную кинематическую пару.
Штриховой линией показаны крайние положения механизма при крайнем верхнем (квп) и крайнем нижнем (кнп) положениях ползуна. Геометрические параметры механизма суть радиус кривошипа R, длина шатуна L и смещение оси перемещения ползуна E, называемоеэксцентриситет или дезаксиал. Принято считать эксцентриситет (дезаксиал) положительным, если он направлено в сторону вращения кривошипа в его нижнем положении и отрицательным, если он направлено против вращения кривошипа. Механизм однозначно определяется двумя параметрами, представляющими собой относительные величины
![]() – коэффициент шатуна;
– коэффициент шатуна;
![]() – степень дезаксиала.
– степень дезаксиала.
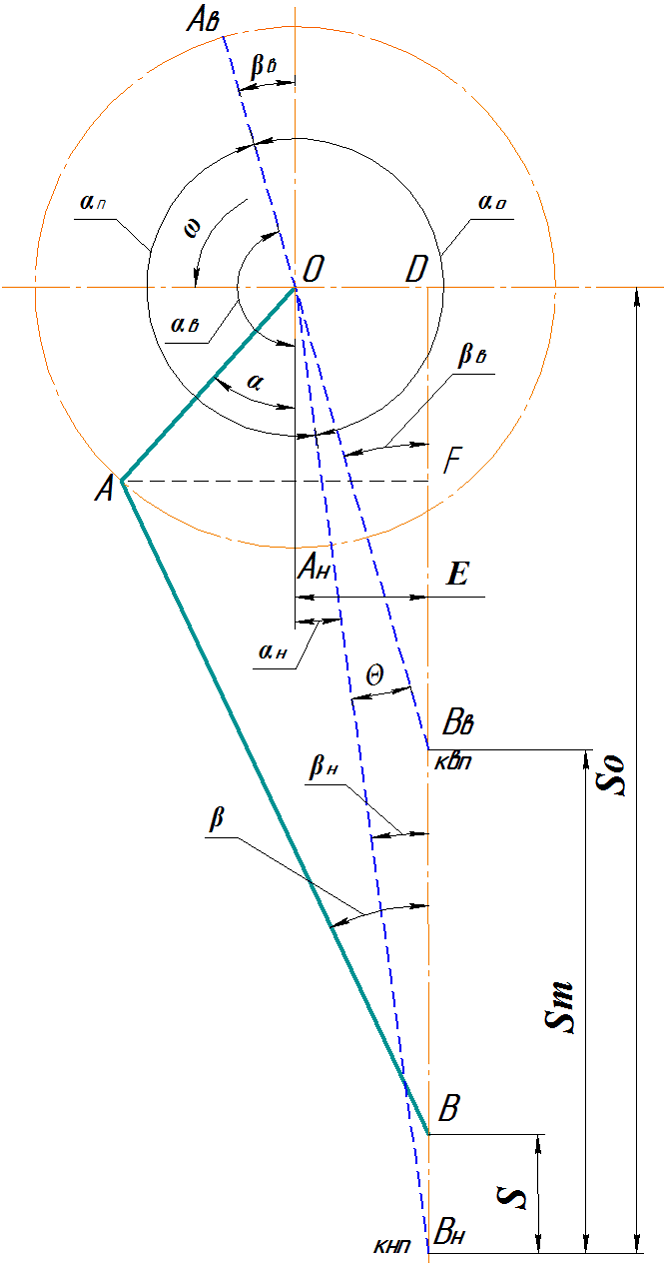
Рис. 1 – Расчетная схема дезаксиального кривошипно-ползунного механизма
Условие существования механизма запишется в виде ![]() , или в относительных единицах
, или в относительных единицах ![]() .
.
Отсюда следует, что значения параметров λ и ε должны удовлетворять условиям
Знак равенства соответствует предельному механизму, существование которого возможно, но функционирование невозможно вследствие недопустимых углов давления. По этой причине условия существования (1) изменены
где Ko – коэффициент ослабления.
Некоторые авторы предлагают значение принимать равным 0,75 [3]. Учитывая, что практические значения коэффициентов λ и ε гораздо меньше предельных, что обеспечивает нормализованные значения углов давления, считаем возможным принимать значение коэффициента равным 0,85…0,9. Зависимость параметров механизма λ и ε при Ko = 0,9 показана на рис. 2.
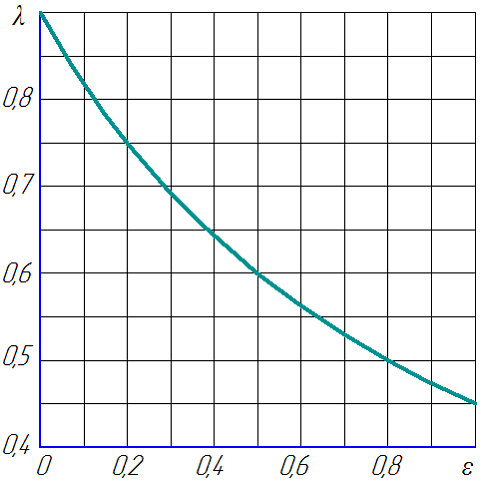
Рис. 2 – Условие существования механизма
Произвольное положение механизма описывается независимой координатой α и производными координатами β (угол наклона шатуна) и S(перемещение ползуна). Угол поворота кривошипа отсчитывается так, как принято в теории кривошипных прессов – против движения кривошипа. Заметим, что при положительном дезаксиале в кнп угол α отрицательный, а при отрицательном дезаксиале – положительный.
Первая задачи анализа механизма состоит в определении функции положения и передаточных функций. Функция положения представляет собой аналитическую зависимость перемещения ведомого звена (ползуна) в функции координаты положения ведущего звена (кривошипа), т. е. зависимость ![]() .
.
Текущее перемещение ползуна определяется по формуле
где длина отрезка S0=DBн есть длина катета прямоугольного треугольника ODBн
Углы α и β взаимосвязаны соотношением, которое следует из равенства отрезка AF для двух треугольников ![]() , откуда следует
, откуда следует ![]() , т. е.
, т. е.
Подставляя значение отрезка SО, после преобразований находим
.gif) . (4)
. (4)Передаточные функции представляют собой первую и вторую производные функции положения по независимой координате α![]()
Для их определения предпочтительно дифференцирование неявной функции ![]() по следующим формулам [4]
по следующим формулам [4]
.gif) (5)
(5)Функция ![]() записывается в виде
записывается в виде
Частные производные будут иметь вид
.gif)
Производные угла β определяются дифференцированием выражения (3) по переменной α
Подставляя производные в уравнения (5), после преобразований находятся
.gif) . (7)
. (7)Произведение первой передаточной функции на угловую скорость ω ведущего звена есть скорость выходного звена, т. е. ползуна
Произведение второй передаточной функции на квадрат угловой скорости ведущего звена при условии ее постоянства есть ускорение ползуна
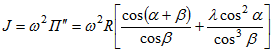 . (9)
. (9)Формулы (4), (8) и (9) являются точными формулами для определения кинематических характеристик дезаксиального механизма. Очевидно, что при ε= 0 имеем частный случай для аксиального механизма.
Для практических расчетов используются упрощенные формулы, полученные разложением в биномиальный ряд подкоренного выражения в формуле (4) и ограничением первыми двумя составляющими
Учитывая, что ![]() , формула (4) упрощается к виду
, формула (4) упрощается к виду
.gif) .
.При реальных значениях коэффициентов λ < 0,4 и ε < 0,6 последней составляющей можно пренебречь и тогда окончательная упрощенная формула для определения перемещения ползуна будет иметь вид
После двукратного дифференцирования выражения (10) по времени, принимая, что ![]() , находятся упрощенные выражения для определения скорости и ускорения ползуна
, находятся упрощенные выражения для определения скорости и ускорения ползуна
Наибольшая погрешность при расчете по упрощенным формулам при реальных значениях коэффициентов λ и ε не превышает 3-5 %.
Следующая задача анализа механизма состоит в определении обратной зависимости угла поворота кривошипа в функции перемещения ползуна, т. е. зависимости ![]() , которая используется при синтезе механизма, энергетических расчетах привода пресса.
, которая используется при синтезе механизма, энергетических расчетах привода пресса.
Из треугольника AFB находим ![]() . Из многоугольника OAFD находим тот же отрезок как
. Из многоугольника OAFD находим тот же отрезок как ![]() . Приравнивая полученные значение, после преобразований находим зависимость между текущим перемещением ползуна и углом поворота кривошипа в виде тригонометрического уравнения
. Приравнивая полученные значение, после преобразований находим зависимость между текущим перемещением ползуна и углом поворота кривошипа в виде тригонометрического уравнения
решение которого будет [5]
Здесь обозначено A, B, С – константы, определяемые по формулам
Два решения соответствуют двум значениям угла α поворота кривошипа, при которых ползун имеет величину смещения S.
Для аксиального механизма при Е = 0, зависимость (11) приводится к виду, известному из учебников по кривошипным прессам [6, 7]
.gif) . (14)
. (14)Третья задача анализа механизма состоит в определении положений звеньев механизма, соответствующих экстремальным значениям перемещения, скорости и ускорения ползуна. В дезаксиальном механизме крайние положения ползуна достигаются при углах поворота кривошипа, отличных от 0 и 180°. Из рисунка 1 следует, что
Полное перемещение ползуна Sm можно определить по формуле (4) или (10) используя значения углов крайних положений кривошипа. Однако проще значение Sm определить как разность двух катетов прямоугольных треугольников ODBн и ODBв
Используя разложение корней в биномиальный ряд с точностью до второго члена ряда, после упрощений находится
.gif) . (17)
. (17)Из формулы следует, что в дезаксиальном механизме величина радиуса кривошипа несколько меньше половины полного перемещения ползуна, т. е. незначительно снижается вертикальный габарит исполнительного механизма.
Экстремальные значения скорости и ускорения ползуна и соответствующие углы поворота кривошипа ввиду сложных математических зависимостей можно определить аналитически только для аксиального механизма.
Максимальное значение скорости достигается при равенстве нулю ее первой производной. Из уравнения (12) следует, что это положение определяется из уравнения ![]() , которое приводится к квадратному уравнению
, которое приводится к квадратному уравнению ![]() , имеющему корни относительно угла αэV
, имеющему корни относительно угла αэV
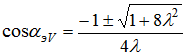 . (18)
. (18)Первый корень ![]() после разложения подкоренного выражения в биномиальный ряд и ограничения первыми двумя членами приводится к виду
после разложения подкоренного выражения в биномиальный ряд и ограничения первыми двумя членами приводится к виду ![]() . Таким образом, максимум скорости имеет место при угле поворота кривошипа примерно
. Таким образом, максимум скорости имеет место при угле поворота кривошипа примерно
Величина угла αэV, определенная по приближенной зависимости (19) меньше, чем по точной зависимости (18), но при λ < 0,3 погрешность составляет не более 3,5 %. Второй корень квадратного уравнения не существует, т. к. значение аргумента косинуса ![]() , что недопустимо.
, что недопустимо.
Максимальное значение скорости при α = αэV равно
Экстремальные значения ускорения ползуна имеют место при равенстве нулю его первой производной, т. е. эти положения определяются из уравнения![]() , которое приводится к виду
, которое приводится к виду
и имеет два корня. Первый корень ![]() , т. е. соответствует положениям кривошипа в крайнем верхнем и крайнем нижнем положениях
, т. е. соответствует положениям кривошипа в крайнем верхнем и крайнем нижнем положениях ![]() . Величина ускорения при этом составляет в крайнем верхнем положении (αэJ = π)
. Величина ускорения при этом составляет в крайнем верхнем положении (αэJ = π)
В крайнем нижнем положении (αэJ = 0) ускорение составляет
Второй корень уравнения (21)
существует при ![]() . При этом положении кривошипа величина ускорения составляет
. При этом положении кривошипа величина ускорения составляет
График изменения ускорения при ![]() при положении кривошипа вблизи крайнего верхнего положения приобретает седловину.
при положении кривошипа вблизи крайнего верхнего положения приобретает седловину.
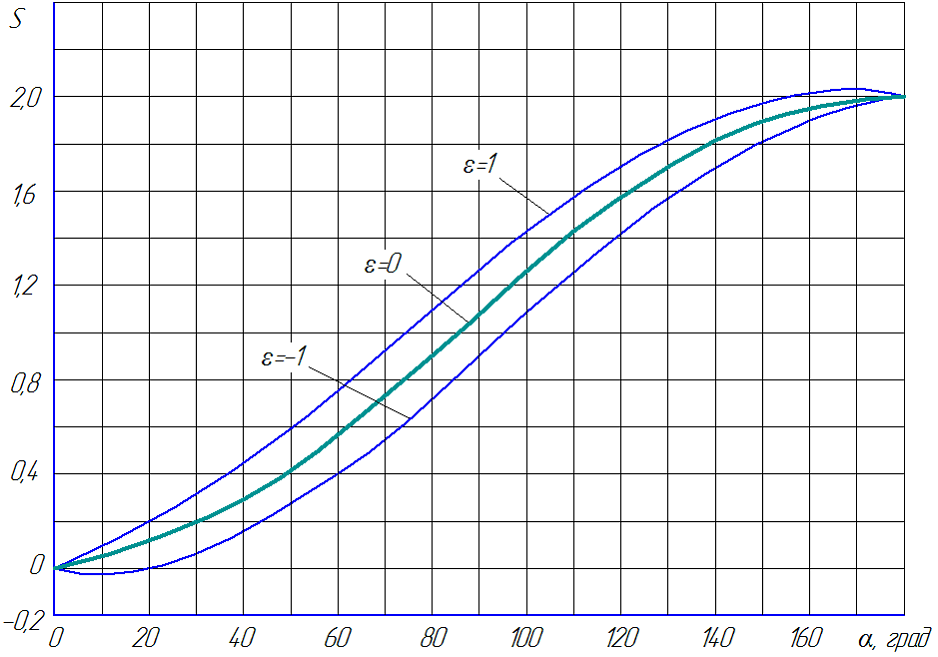
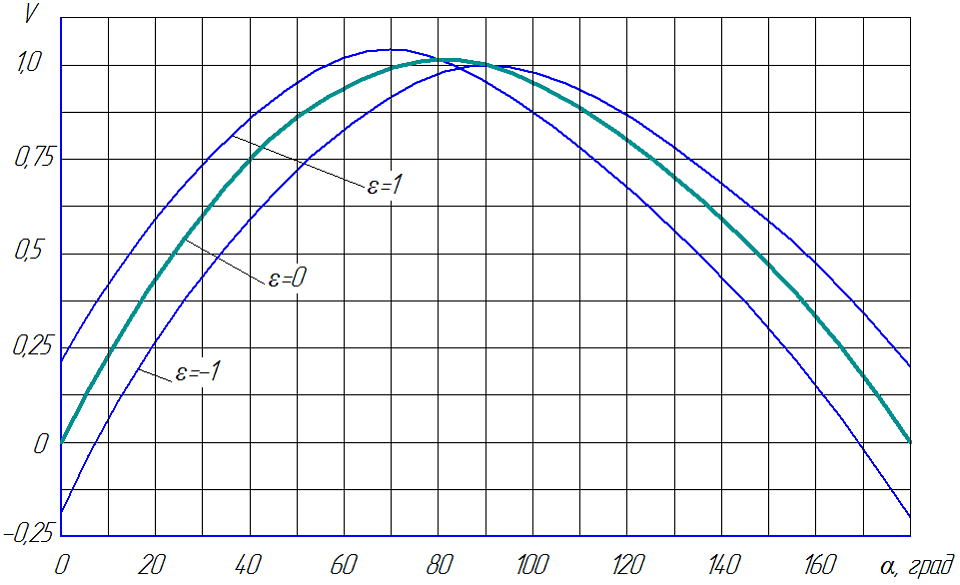
Полученные точные и упрощенные формулы однозначно определяют кинематические характеристики дезаксиального кривошипно-ползунного механизма. Полагая величину эксцентриситета равной нулю, из полученных зависимостей следуют частные формулы для расчета аксиального механизма. Сопоставление этих зависимостей показывает основные отличия кинематических показателей дезаксиального механизма от аксиального. На рис. 3 показаны графики изменения перемещения, скорости и ускорения ползуна при R = 1, ω = 1, λ = 0,2 и различных значениях степени дезаксиала ε.
Характер перемещения ползуна дезаксиального механизма практически не изменяется по сравнению с аксиальным механизмом при положениях кривошипа, близких к крайним положениям. При увеличении коэффициента эксцентриситета ε от -0,5 до +0,5 наибольшая разность перемещений механизмов составляет не более 7% при углах кривошипа около 90°. Полное перемещение ползуна при этом увеличивается не более чем на 2%. С увеличением величины дезаксиала максимальное значение скорости изменяется на несколько процентов в зависимости от знака эксцентриситета. Положение экстремума скорости при снижении значения ε смещается ближе к углу кривошипа, равном π/2. Величина ускорения в кнп не зависит от степени дезаксиала и определяется по формуле (45). В положениях, близких к квп при положительных значениях дезаксиала возникает седловина, а значение ускорения в положении третьего экстремума превышает расчетное значение по формуле (25) для центрального механизма на 5–7 %.
Из графика изменения скорости ползуна (рис. 3, б) следует одно очень важное обстоятельство. Некоторые операции штамповки (вытяжка, чистовая вырубка, холодная объемная штамповка, выдавливание и др.) накладывают ограничения на максимальную скорость ползуна в период рабочего хода. По этой причине приходится ограничивать число ходов пресса, что, естественно, уменьшает их производительность. При горячей объемной штамповке наоборот, время контакта инструмента с нагретым металлом должно быть минимальным, поэтому скорость рабочего хода желательно увеличивать. В дезаксиальном механизме длительность прямого и обратного хода различны. В этом случае за счет изменения длительности холостого или рабочего хода можно регулировать производительность пресса или обеспечивать более благоприятные условия работы инструмента.
При заданной средней скорости прямого хода ползуна Vп длительность прямого хода составляет ![]() . Длительность холостого обратного хода определяется как
. Длительность холостого обратного хода определяется как ![]() . Коэффициент Kv, равный отношению средней скорости прямого хода к средней скорости обратного (холостого) хода
. Коэффициент Kv, равный отношению средней скорости прямого хода к средней скорости обратного (холостого) хода ![]() , называется коэффициент средней скорости.
, называется коэффициент средней скорости.
Коэффициент Kv определяется через углы крайних положений кривошипа. Если принять скорость вращения кривошипа ω постоянной, то длительность прямого или обратного хода пропорциональна соответствующему углу поворота кривошипа, т. е. ![]() , и тогда
, и тогда ![]() .
.
б)

в)
Рис. 3 – Кинематические характеристики кривошипно-ползунного механизма
а) – перемещение ползуна; б) – скорость ползуна; в) – ускорение ползуна
Из рисунка 1 следует, что углы поворота кривошипа при прямом и обратном ходе ![]() и
и ![]() . Угол между крайними положениями кривошипа
. Угол между крайними положениями кривошипа
Таким образом, коэффициент средней скорости однозначно определяется только значениями коэффициентов λ и ε , т. е.
При положительном эксцентриситете угол θ положительный и Kv <1, при отрицательном эксцентриситете угол θ отрицательный и Kv >1.
Длительность двойного хода
Т. к. ![]() , легко определить, что допустимое число ходов nн пресса при ограничении средней скорости прямого хода ползуна будет
, легко определить, что допустимое число ходов nн пресса при ограничении средней скорости прямого хода ползуна будет
Для аксиального механизма Kv = 1 и тогда допустимое число ходов ![]() . Соотношение числа ходов дезаксиального и аксиального механизмов при одинаковой скорости прямого хода будет
. Соотношение числа ходов дезаксиального и аксиального механизмов при одинаковой скорости прямого хода будет
Из этой формулы следует, что для увеличения допустимого числа ходов рационально использовать механизмы с отрицательным дезаксиалом. Пределом увеличения числа ходов является ![]() при
при ![]() . Практически при Kv ≤ 1,25 число ходов может быть увеличено более чем в 1,1 раза. Важным является то, что скорость в период рабочего хода, т. е. при углах кривошипа менее 60°, меньше, чем в аксиальном механизма, а при углах более 90° – больше.
. Практически при Kv ≤ 1,25 число ходов может быть увеличено более чем в 1,1 раза. Важным является то, что скорость в период рабочего хода, т. е. при углах кривошипа менее 60°, меньше, чем в аксиальном механизма, а при углах более 90° – больше.
Проектирование рычажных силовых механизмов, к которым относятся и кривошипно-ползунные, предполагает обязательную проверку углов давления в кинематических парах. Как известно, угол давления есть угол между направлением действия силы и вектором скорости точки приложения этой силы в кинематической паре [2]. Угол, дополняющий угол давления до 90°, называется углом передачи. Во избежание заклинивания и уменьшения сил трения рекомендуется максимальное значение угла давления для прямого хода ограничивать величиной 30°, а при холостом ходе – не более 45°.
В рассматриваемом механизме угол давления в кинематической паре соединения шатуна с ползуном (точка В) есть угол β, величина которого определяется по формуле (3). Практический интерес представляют пять значений угла давления (рис. 4) – в крайнем нижнем δн и крайнем верхнем δвположении кривошипа, в крайнем левом (при α = π/2) δл и крайнем правом (при α = 3π/2) δп положении кривошипа, а также в начале рабочего хода δр(при α = αр).
Значения углов давления в крайних положениях определяются по формулам (15) и (16), т. к. ![]() и
и ![]() . Угол давления в начале рабочего хода определяется по формуле (3) при заданном угле начала рабочего хода (α = αр) или положении ползуна в начале рабочего хода (S = Sнр). В последнем случае по формуле (13) или (14) определяется угол αр, а затем находится угол давления δр. В крайнем левом или правом положениях кривошипа величина углов давления находится по формуле
. Угол давления в начале рабочего хода определяется по формуле (3) при заданном угле начала рабочего хода (α = αр) или положении ползуна в начале рабочего хода (S = Sнр). В последнем случае по формуле (13) или (14) определяется угол αр, а затем находится угол давления δр. В крайнем левом или правом положениях кривошипа величина углов давления находится по формуле
где верхний знак (плюс) принимается для левого положения кривошипа (α = π/2), а нижний (минус) – для правого положения.
Степень дезаксиала в расчетных формулах принимается с соответствующим знаком, потому при определенных условиях угол давления отрицательный, что свидетельствует о том, что шатун в расчетном положении отклоняется вправо от вертикальной линии перемещения ползуна.
При практических значениях коэффициентов λ и ε, удовлетворяющих условию (2), величина угла давления никогда не превышает максимально допустимые значения. В аксиальном механизме максимальный угол давления при прямом и обратном ходе равен ±30° при коэффициенте λ = 0,5, а при значениях коэффициента λ меньше 0,2 угол давления не превышает ±15°.
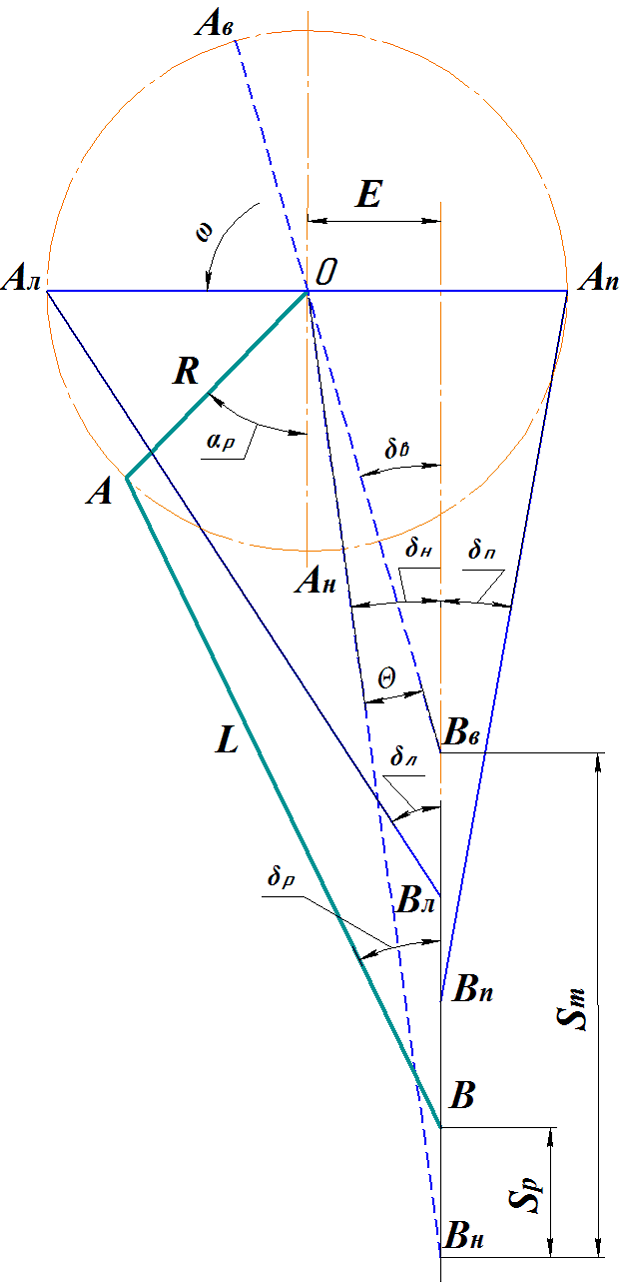
Рис. 4 – Углы давления в кривошипно-ползунном механизме
При отрицательном дезаксиале значение угла давления на участке прямого хода становится меньше, чем в аксиальном механизме. Даже при максимальных значениях коэффициентов λ = 0,5 и ε = −0,5 угол давления не превышает 15°. Этот вывод еще раз показывает эффективность использования отрицательного дезаксиального механизма в листоштамповочных прессах.
В положительном дезаксиальном механизме угол давления при прямом ходе возрастает, а при обратном уменьшается по сравнению с аксиальным механизмом. Тем не менее, даже при λ = 0,3 и ε = 0,5 угол давления при прямом ходе меньше 28°.
Основным недостатком дезаксиальных механизмов считается увеличенное давление на направляющие. Увеличение сил трения в направляющих действительно приводит к увеличенному износу контактируемых поверхностей.
Однако для кривошипных прессов для горячей объемной штамповки (КГШП, ГКМ) увеличение угла давления при прямом ходе является скорее преимуществом, чем недостатком. Так, в процессе холостого и рабочего хода ползун может занимать любое положение относительно направляющих в зависимости от величины зазоров и расположения равнодействующей внешних сил. Для увеличения его устойчивости и, как следствие, улучшения направления инструмента необходимо обеспечить постоянное гарантированное его расположение относительно направляющих, по крайней мере, в период рабочего хода.
Во-первых, в связи с определенным смещением технологической нагрузки относительно оси ползуна дезаксиал является наиболее действенным средством управления положением ползуна, т. е. средством контролируемого управления качеством работы штампов и, как результат, качеством изделия.
Во-вторых, в кривошипном прессе сила давления на направляющие может быть уменьшена оптимальным выбором геометрических параметров ГИМа. В-третьих, износ происходит не по всей поверхности направляющих, а преимущественно на кромках ползуна и определяется не столько величиной нормальной силы, а столько размерами контактной поверхности. Эта задача требует дополнительного анализа с привлечением положений теории контактной прочности машин.
1. Получены аналитические зависимости для определения основных кинематических характеристик кривошипно-ползунного дезаксиального механизма, необходимые для синтеза и анализа исполнительных механизмов кривошипных прессов.
2. Использование дезаксиального исполнительного механизма с отрицательным дезаксиалом позволяет увеличить наибольшее число ходов листоштамповочных прессов до 8-10 % при соблюдении установленной скорости рабочего хода.
3. Величина угла давления в кинематических парах механизма при реальных значениях геометрических параметров не превышает рекомендуемые значения.
4. Использование дезаксиального механизма по сравнению с аксиальным механизмом не требует практически никаких материальных затрат и изменения конструкции узлов пресса.
Библиографический список
- Левитский Н.И. Теория механизмов и машин / Н.И. Левитский. –М.: Наука, 1979. – 576 с.
- Артоболевский И.И. Теория машин и механизмов / И.И. Артоболевский. –М.: Наука, 1988. – 640 с.
- Семенов М.В. Кинематические и динамические расчеты исполнительных механизмов / М.В. Семенов. – Л.: Машиностроение, 1974. – 432 с.
- Вульфсон И.И. Динамические расчеты цикловых механизмов / И.И. Вульфсон. —Л.: Машиностроение, 1976. — 328 с.
- Выгодский М.Я. Справочник по математике / М.Я. Выгодский. — М.: АСТ: Астрель, 2010. — 1055 с.
- Живов Л.И. Кузнечно-штамповочное оборудование: Учебник для вузов / Л.И. Живов, А.Г. Овчинников, Е.Н. Складчиков / Под ред. Л.И. Живова. – М.: Изд-во МГТУ, 2006. – 560 с.
- Рей Р.И., Монятовский С.С. Кузнечно-штамповочное оборудование. Прессы кривошипные. – Луганск : Изд-во ВНУ, 2000. – 216 с.