Большинство процессов имеющих естественную или техническую природу подчиняются сложным законам. Определение этих процессов приводит к необходимости решения многокомпонентных задач, установлению сложных параметрических зависимостей, что в свою очередь приводит к значительным сложностям в построении математических моделей.
Процесс выявления такого рода многофакторных зависимостей осуществляется посредством экспериментальных данных. При этом большое число параметров в исследуемой модели не только приводит к сложности расчетов, но также и существенно снижает наглядность модели как таковой.
Решением данной проблемы может служить метод геометрического моделирования. Данный метод является наиболее актуальным в качестве представления сложных динамических процессов и систем с соответствующим прогнозом динамики. Метод позволяет находить неизвестное значение функции при условии известности соотношений, связывающих данную функцию и ее производные на их геометрических моделях.
В качестве моделей наиболее часто используют статистические и аппроксимационные модели, построенные на данных полученных в ходе экспериментов. Аналитическое представление данных моделей затруднительно для понимания наглядности процесса, поэтому целесообразно осуществить их перевод в геометрический аналог.
Решением задачи геометрического моделирования выступает конструкция, представленная в многомерном геометрическом пространстве. Расположение элементов конструкции однозначно определяет соотношения аргументов и функции в сложных многопараметрических системах.
Наиболее частыми решениями выступают алгебраические и дробно-алгебраические поверхности, описываемые полиноминальными или дробно-полиноминальными зависимостями соответственно.
Разработка геометрической модели загрязнения атмосферного воздуха начинается с выявления временных уровней со значительным превышением концентраций загрязняющих веществ. При этом учитывая разность в переносе отдельных компонентов целесообразно проводить исследования не по комплексным показателям типа ИЗА-5, а по отдельным составляющим ИЗА или ПДК [1]. Следующим этапом является установление корреляционных связей между отдельными метеорологическими параметрами с каждым из загрязнителей и комплексным показателем загрязнения. При этом необходимо учитывать также совместное влияние факторов [2].
В качестве основных факторов влияющих на загрязнение атмосферы были выбраны следующие метеорологические показатели: влажность, скорость ветра, количество осадков, температура. Помимо прочего учитывается и временной характер изменения концентраций.
В качестве исследуемого параметра в модели выступает концентрация пяти приоритетных загрязнителей, которыми в зависимости от исследуемого города могут выступать различные компоненты.
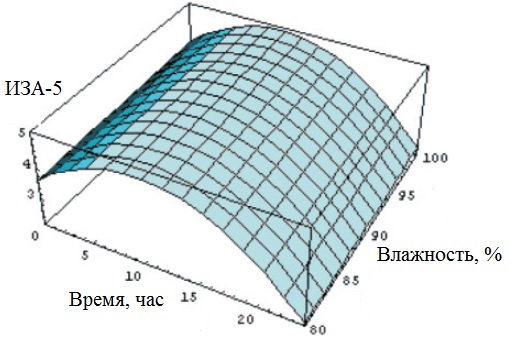
Пример временной зависимости ИЗА-5 от влажности представлен на рисунке 1:
Рисунок 1. – Динамика изменения ИЗА-5 от влажности во времени
Данная поверхность представляет собой наиболее простой пример геометрического моделирования отдельных параметров. В случае многокомпонентности факторов наиболее целесообразно рассматривать ряд поверхностей или проекции гиперкубов в зависимости от количества исследуемых параметров.
Библиографический список
- Голубничий А.А. (2014) К вопросу о некоторых особенностях нормирования качества атмосферного воздуха в Российской Федерации // «Dny vedy – 2014». d.11 Pravni vedy – ss. 10-12.
- Голубничий А.А., Замулина М.В. (2015) Учет климатических параметров при распространении аэрозоля в рамках ОНД-86 // Современная техника и технологии. 2015. № 1 [Электронный ресурс]. URL: http://technology.snauka.ru/2015/01/5631 (дата обращения: 23.02.2015).