При рассмотрении фильтрации аномальных жидкостей существенную роль играет пористая среда. Взаимодействие фильтрующейся жидкости с материалом скелета приводит к изменению реологических параметров жидкости (например, вязкости жидкости) или пористой среды. Из-за вышеперечисленных эффектов появляются фильтрационные аномалии и в этом случае речь идет уже не о фильтрации данной жидкости, а о поведении системы “жидкость – пористая cреда”.
С учетом этого Мирзаджанзаде А.Х. предложил феноменологическую теорию фильтрации вязкопластичной жидкости, в основе которой лежит линейная модель вязкопластичной сплошной среды. Движение указанной сплошной среды описывается следующим законом фильтрации:
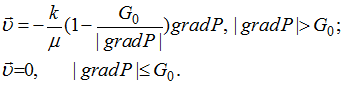 (1)
(1)
Предельное значение 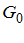 определяет ту величину градиента давления, по достижении которой начинается движение жидкости; при меньших значениях градиента движение отсутствует. Его значение определяется соотношением
определяет ту величину градиента давления, по достижении которой начинается движение жидкости; при меньших значениях градиента движение отсутствует. Его значение определяется соотношением
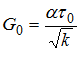 , (2)
, (2)
где 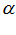 – некоторая постоянная, k - проницаемость,
– некоторая постоянная, k - проницаемость, 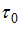 - предельное напряжение сдвига.
- предельное напряжение сдвига.
Уравнение для давления при упругом режиме пласта можно получить, дополняя закон фильтрации (1) уравнением неразрывности, уравнением состояния флюида и пористой среды [1, c. 53].
Искомое дифференциальное уравнение для определения давления имеет вид :
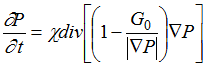 ,
, 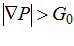 , (3)
, (3)
где 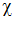 – коэффициент пьезопроводности.
– коэффициент пьезопроводности.
При решении таких задач на основе вышепредложенной модели фильтрации, то есть с предельным градиентом давления, в пласте образуется такая область фильтрации жидкости, на границе которой модуль градиента давления должен равняться предельному градиенту 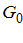 [2, c.4]. Ниже рассмотрены случаи аналитического нахождения распределения давления в аномальных жидкостях.
[2, c.4]. Ниже рассмотрены случаи аналитического нахождения распределения давления в аномальных жидкостях.
Движение аномальных жидкостей в пластах по закону (1) приводит к существенному изменению распределения полей давления [1, с.134],[3].
Рассмотрим плоскорадиальный приток в скважину аномальной (в частности, вязкопластичной) жидкости. Закон (1) перепишем в виде, для стационарного решения:
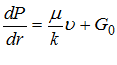 , при
, при 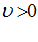 , (4)
, (4)
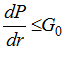 , при
, при 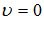 .
.
Учитывая, что дебит сважины в круговом пласте
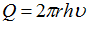 , (5) имеем
, (5) имеем
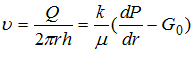 , если
, если 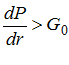
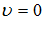 , если
, если 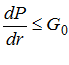 (6)
(6)
Cчитаем известным давление на забое пласта
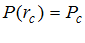 ,
,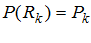 . (8)
. (8)
Из уравнения (1.15) находим :
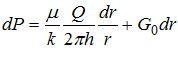 ,
,
откуда после интегрирования получим распределение давления в пласте
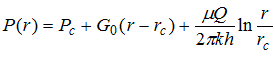 ,
, 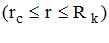 . (9)
. (9)
Аналогично найдем распределение давления для линейной фильтрации:
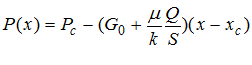 (10)
(10)
и для радиально-сферического течения:
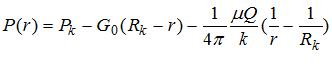 (11)
(11)
Полученные аналитические решения распределения давления представляет большой интерес для изучения температурных полей в аномальных жидкостях.
Библиографический список
-
Басниев К.С., Кочина И.Н., Максимов В.М. Подземная гидродинамика. М.: Недра, – 1993. – 416 c.
-
Хусаинова Г.Я. Исследование температурных полей при фильтрации аномальных жидкостей. Автореферат диссертации на соискание ученой степени кандидата физико-математических наук. – Уфа. – 1998. – 14 с.
- Хусаинова Г.Я. Исследование температурных полей аномальных жидкостей // NovaInfo.Ru (Электронный журнал.) – 2015 г. – № 35; URL: http://novainfo.ru/archive/35/issledovanie-temperaturnykh-poley-anomalnykh-zhidkostey (дата обращения 19.06.1015 )
