Основными источниками энергии XXI века выступают нефть и газ, добывающиеся из глубоко залегающих подземных пластов. Описание процессов накопления и фильтрации нефти и газа в таких пористых пластах, а также основные технологии их добычи представляют собой важные задачи теории фильтрации.
В настоящее время закачку газа в пористый пласт используют в нескольких случаях.
Во-первых, данный способ может быть использован как один из вариантов утилизации попутного нефтяного газа при разработке нефтяных месторождений (стоит, конечно, отметить, что попутный нефтяной газ эффективнее переработать, чем утилизировать, – так, некоторые компании уже разработали и запатентовали оборудование по переработке такого газа).
Во-вторых, в продуктивных коллекторах, имеющих в своем составе много глинистого материала, закачка воды для поддержания пластового давления, как правило, становится неэффективной (такие нагнетательные скважины требуют специальной обработки воды и высоких давлений нагнетания). В этих условиях закачка сухого углеводородного газа будет гораздо эффективнее, так как такой газ не будет взаимодействовать с породами коллектора, а значит, обеспечит технически приемлемые параметры процесса.
В-третьих, закачка горячего газа может быть использована для добычи углеводородного сырья из газогидратных месторождений. Энергетическая эффективность такого процесса показана в работах [1, 2].
Кроме перечисленных случаев имеются и другие области, где используется процесс нагнетания газа в пористый пласт или энергия СВЧ-излучения [3] с целью достижения тех или иных целей.
Так, например, в работе [4] рассмотрена плоская одномерная задача об инжекции влажного пара в пористую среду, исследовано влияние параметров, определяющих начальное состояние пористой среды, граничного давления, температуры и влагосодержания пара на темп распространения гидродинамических и температурных полей через границу пористой среды без учета эффектов связанных с тепловым разрушением твердой фазы.
В связи с актуальностью и повсеместным использованием метода закачки газа в пористый пласт, рассмотрим более детально данный процесс в плоском и радиальном одномерных случаях.
Рассмотрим пласт, представляющий собой пористую среду. Через границу области газонасыщенной пористой среды происходит закачка горячего газа. Будем полагать, что эта граница неподвижна.
При описании процессов фильтрации и тепломассопереноса примем следующие допущения: скелет пористой среды несжимаем и неподвижен, пористость постоянна, газ – калорически совершенный, фильтрационные процессы – однотемпературные (температура газа и пористой среды в каждой точке совпадают). В рамках отмеченных допущений запишем для одномерных задач уравнения сохранения массы, притока тепла, закон Дарси и уравнение состояния газа:
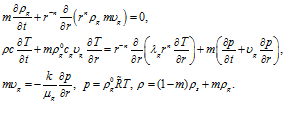 (1)
(1)
Здесь 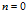 или
или 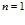 соответствуют плоской и радиальной задачам. Нижний индекс 0 соответствует значениям параметров для начального невозмущенного состояния, а верхний индекс 0 определяет истинное состояние параметра. Нижние индексы
соответствуют плоской и радиальной задачам. Нижний индекс 0 соответствует значениям параметров для начального невозмущенного состояния, а верхний индекс 0 определяет истинное состояние параметра. Нижние индексы 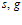 относятся соответственно к пористому скелету и газу (skeleton, gas). В этих обозначениях
относятся соответственно к пористому скелету и газу (skeleton, gas). В этих обозначениях 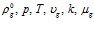 – истинная плотность, давление, температура, скорость фильтрации, коэффициент абсолютной проницаемости и динамическая вязкость газа соответственно,
– истинная плотность, давление, температура, скорость фильтрации, коэффициент абсолютной проницаемости и динамическая вязкость газа соответственно, 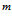 – пористость среды,
– пористость среды, 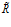 – приведенная газовая постоянная (своя для каждого газа:
– приведенная газовая постоянная (своя для каждого газа: 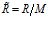 ,
, 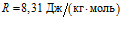 ,
, 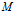 – молярная масса газа),
– молярная масса газа), 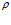 и
и 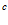 – средняя плотность и теплоемкость системы «пористая среда – газ».
– средняя плотность и теплоемкость системы «пористая среда – газ».
Будем полагать, что в начальный момент времени в пористой среде, заполненной газом, давление 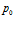 и температура
и температура 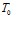 однородны. Эти условия запишем в виде:
однородны. Эти условия запишем в виде:
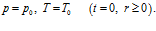 (2)
(2)
Для плоской задачи 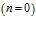 будем полагать, что на границе пористой среды в момент времени
будем полагать, что на границе пористой среды в момент времени 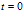 давление на границе
давление на границе 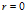 повышается до значения
повышается до значения 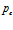 и в дальнейшем поддерживается постоянным, а температура закачиваемого газа равна
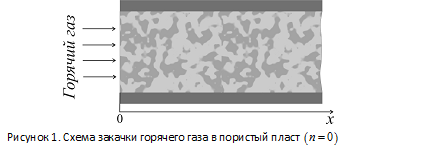
и в дальнейшем поддерживается постоянным, а температура закачиваемого газа равна 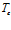 (рис. 1):
(рис. 1):
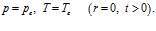 (3)
(3)
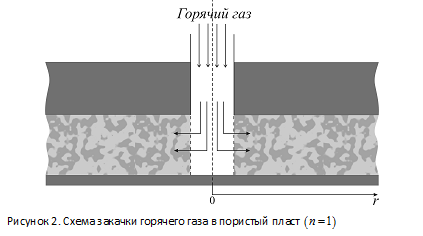
В случае радиальной задачи рассмотрим однородный, горизонтальный пласт постоянной толщины и неограниченной протяженности, представляющий собой пористую среду, заполненную газом. Кровля и подошва пласта непроницаемы. В пласте пробурена скважина, вскрывающая пласт на всю толщину. Через скважину закачивается теплый газ с постоянным массовым расходом 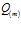 , отнесенным на единицу длины скважины (рис. 2).
, отнесенным на единицу длины скважины (рис. 2).
В момент времени  начинается нагнетание газа с постоянным массовым расходом
начинается нагнетание газа с постоянным массовым расходом 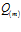 :
:
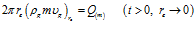 . (4)
. (4)
С учётом закона Дарси и уравнения калорически совершенного газа, (4) запишем в виде:
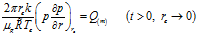 . (5)
. (5)
Оценки показывают, что в большинстве случаев, представляющих практический интерес, в уравнении притока тепла можно пренебречь слагаемыми, связанными с баротермическим эффектом. Кроме того, в уравнении пьезопроводности, следующем из уравнения сохранения массы и закона Дарси, слагаемое, учитывающее переменность температуры, мало, если характерные перепады температуры 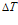 в области фильтрации небольшие (например, при
в области фильтрации небольшие (например, при 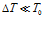 ). В дальнейшем будем также пренебрегать переменностью объемной теплоемкости и коэффициента теплопроводности пористой среды:
). В дальнейшем будем также пренебрегать переменностью объемной теплоемкости и коэффициента теплопроводности пористой среды:
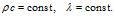 (6)
(6)
Тогда система (1) может быть приведена к виду:
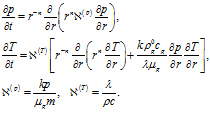 (7)
(7)
Здесь 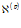 и
и 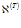 – коэффициенты пьезопроводности и температуропроводности соответственно.
– коэффициенты пьезопроводности и температуропроводности соответственно.
Для плоской задачи система уравнений (7) перепишется в виде:
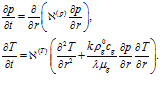 (8)
(8)
В данной постановке задача является автомодельной. Введем автомодельную переменную в виде: 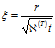 .
.
Перейдем к автомодельным переменным:
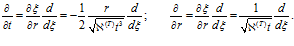
С учетом новых обозначений система (8) примет вид:
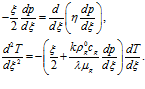 (9)
(9)
Здесь 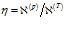 .
.
Применим к первому уравнению системы (9) метод линеаризации Лейбензона, заключающийся в умножении обеих частей уравнения на величину давления 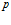 :
:
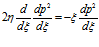 . (10)
. (10)
Проведя замены  и
и 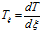 , с учетом (10) систему уравнений (9) перепишем в виде
, с учетом (10) систему уравнений (9) перепишем в виде
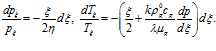 (11)
(11)
Рассмотрим первое уравнение системы (11). Его общее решение имеет вид
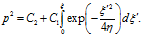
Постоянные 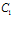 и
и 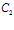 найдем из начальных и граничных условий, которые в автомодельных переменных имеют вид
найдем из начальных и граничных условий, которые в автомодельных переменных имеют вид
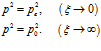 (12)
(12)
Тогда выражение для распределения давления запишется в виде
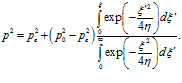 (13)
(13)
Отметим, что при расчетах обычно принимают
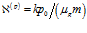 или
или 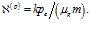
Выражение для распределения температур получается как решение второго уравнения системы (11):
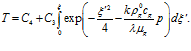
Постоянные 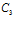 и
и 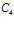 найдутся из условий, аналогичных условиям (12):
найдутся из условий, аналогичных условиям (12):
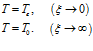
Окончательно для распределения температур запишем:
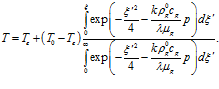 (14)
(14)
Результаты численных расчетов, проведенных по выражениям (13) и (14), представлены ниже на рис. 3 – 6. При этом взяты следующие значения параметров: 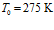 ,
, 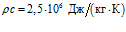 ,
, 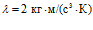 ,
, 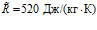 ,
, 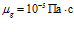 .
.
На рис. 3 проиллюстрировано влияние температуры закачиваемого газа на профили температур в среде. Приведен также профиль давлений, возникающих в процессе закачки газа (от температур не зависит). Графики построены для следующих значений параметров среды: 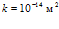 ,
, 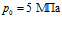 ,
, 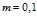 . Давление закачиваемого газа
. Давление закачиваемого газа 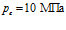 . Линии 1, 2 и 3 соответствуют температурам закачиваемого газа
. Линии 1, 2 и 3 соответствуют температурам закачиваемого газа 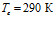 ,
, 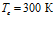 и
и 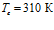 соответственно. Видно, что с ростом температур закачиваемого газа увеличивается угол наклона кривых к оси
соответственно. Видно, что с ростом температур закачиваемого газа увеличивается угол наклона кривых к оси 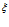 (растет крутизна кривых), однако выравнивание температур с исходной пластовой происходит практически в одной и той же координате
(растет крутизна кривых), однако выравнивание температур с исходной пластовой происходит практически в одной и той же координате 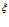 . Последний факт означает, что характерная глубина проникания температурных волн практически не зависит от температуры закачиваемого газа. На основе приведенных графиков и вида автомодельной переменной
. Последний факт означает, что характерная глубина проникания температурных волн практически не зависит от температуры закачиваемого газа. На основе приведенных графиков и вида автомодельной переменной 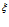 можно определить характерное расстояние
можно определить характерное расстояние 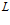 распространения температурной волны за некоторое время
распространения температурной волны за некоторое время 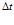 .
.
Рассмотрим, например, линию 3, соответствующую температуре закачиваемого газа 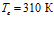 . Выравнивание температур с исходной пластовой соответствует значению автомодельной переменной
. Выравнивание температур с исходной пластовой соответствует значению автомодельной переменной 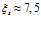 . Для момента времени, например,
. Для момента времени, например, 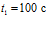 это соответствует координате
это соответствует координате 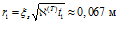 ; моменту времени
; моменту времени  будет соответствовать координата
будет соответствовать координата 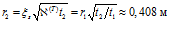 . Таким образом, за время
. Таким образом, за время 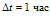 , температурная волна проникает на расстояние
, температурная волна проникает на расстояние 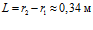 ; за время
; за время 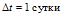 глубина проникания составит около
глубина проникания составит около 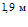 , а за время
, а за время 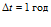 – около
– около 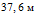 .
.
Аналогичные расчеты для характерного расстояния проникания волны давления дают следующие результаты (на основе приведенного здесь профиля давления). Выравнивание давления с пластовым 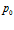 происходит при
происходит при 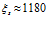 . Отсюда, при
. Отсюда, при 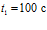 имеем
имеем 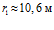 , при
, при 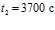 получим
получим 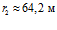 . Таким образом, за время
. Таким образом, за время 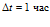 , волна давления проникает на расстояние
, волна давления проникает на расстояние 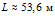 ; за время
; за время 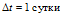 глубина проникания составит около
глубина проникания составит около 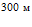 , а за время
, а за время 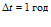 – около
– около  .
.
На рис. 4 представлены профили давлений и температур в среде при различных значениях пластового давления 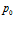 . Параметры пласта:
. Параметры пласта: 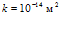 ,
, 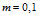 . Температура и давление закачиваемого в пласт газа соответственно равны
. Температура и давление закачиваемого в пласт газа соответственно равны 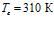 и
и 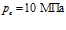 . Линии 1 соответствуют случаю
. Линии 1 соответствуют случаю 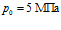 , линии 2 –
, линии 2 – 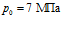 , линии 3 –
, линии 3 – 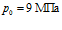 . Видно, что изменение пластового давления приводит к изменению распределения и давлений, и температур в среде. При этом ширина зоны фильтрации не зависит от пластового давления, однако с ростом
. Видно, что изменение пластового давления приводит к изменению распределения и давлений, и температур в среде. При этом ширина зоны фильтрации не зависит от пластового давления, однако с ростом 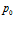 отмечается более резкий спад температур.
отмечается более резкий спад температур.
Рис. 5 демонстрирует влияние проницаемости пористой среды на профили давлений и температур. Графики построены при следующих значениях параметров: 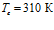 ,
, 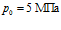 ,
, 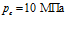 ,
, 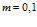 . Линии 1 соответствуют случаю
. Линии 1 соответствуют случаю 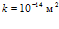 , линии 2 –
, линии 2 – 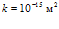 , линии 3 –
, линии 3 – 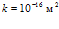 . Как и следовало ожидать, уменьшение проницаемости среды ведет к сужению области фильтрации, и более резкому падению температур. Кроме того, сравнивая между собой глубину проникания волн давлений для проницаемостей среды
. Как и следовало ожидать, уменьшение проницаемости среды ведет к сужению области фильтрации, и более резкому падению температур. Кроме того, сравнивая между собой глубину проникания волн давлений для проницаемостей среды 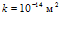 и
и 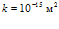 , можно прийти к выводу, что
, можно прийти к выводу, что 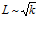 . Действительно, если принять, что проницаемости
. Действительно, если принять, что проницаемости 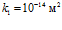 соответствует
соответствует 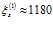 , а проницаемости
, а проницаемости 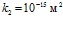 соответствует
соответствует 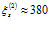 , то получим:
, то получим: 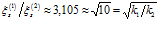 .
.
Если провести соответствующие расчеты еще и для различных значений пористости 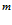 и давления
и давления 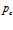 , то можно заметить, что глубина проникания волн давления
, то можно заметить, что глубина проникания волн давления 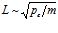 . В итоге приходим к выводу, что
. В итоге приходим к выводу, что 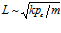 . В общем случае математическая теория показывает, что характерное расстояние
. В общем случае математическая теория показывает, что характерное расстояние 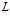 проникания волны давления за время
проникания волны давления за время 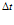 находится как
находится как 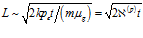 .
.
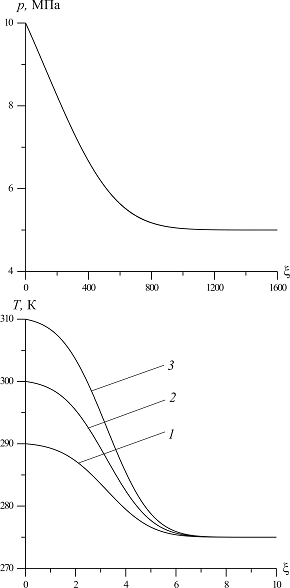
Рисунок 3. Влияние температуры 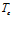 закачиваемого газа на профили давлений и температур в пористой среде. Параметры среды:
закачиваемого газа на профили давлений и температур в пористой среде. Параметры среды: 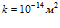 ,
, 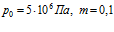 . Параметры закачиваемого газа:
. Параметры закачиваемого газа: 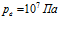 , линии 1 –
, линии 1 – 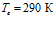 , линии 2 –
, линии 2 – 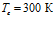 , линии 3 –
, линии 3 – 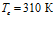 .
.
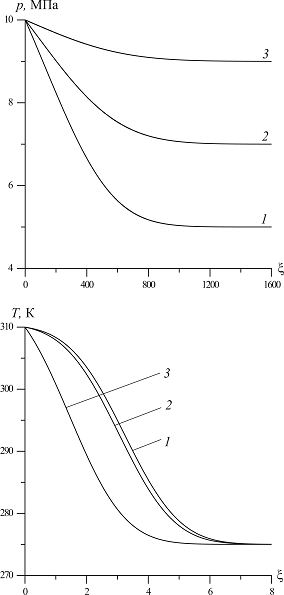
Рисунок 4. Влияние исходного пластового давления на профили давлений и температур в пористой среде. Параметры среды: 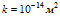 ,
, 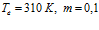 . Параметры закачиваемого газа:
. Параметры закачиваемого газа: 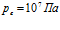 , линии 1 –
, линии 1 – 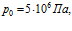 линии 2 –
линии 2 –  линии 3 –
линии 3 – 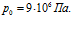
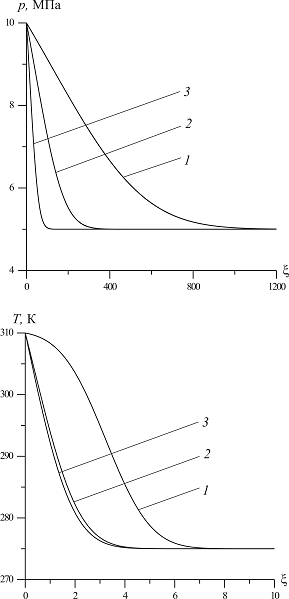
Рисунок 5. Влияние проницаемости среды на профили давлений и температур в пористой среде. Параметры среды: 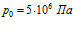 ,
, 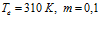 . Параметры закачиваемого газа:
. Параметры закачиваемого газа: 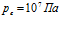 , линии 1 –
, линии 1 – 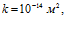 линии 2 –
линии 2 – 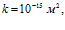 линии 3 –
линии 3 – 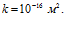
На рис. 6 показано влияние давления закачиваемого газа на профили давлений и температур в среде при следующих значениях параметров: 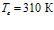 ,
, 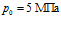 ,
, 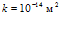 ,
, 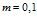 . Линии 1 –
. Линии 1 – 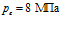 , линии 2 –
, линии 2 –  , линии 3 –
, линии 3 – 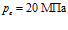 . Видно, что рост давления
. Видно, что рост давления 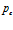 приводит к расширению зоны фильтрации и увеличению ширины зоны перепада температур. При этом при больших значениях давления
приводит к расширению зоны фильтрации и увеличению ширины зоны перепада температур. При этом при больших значениях давления 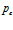 образуется область, в которой температура закачиваемого газа практически не изменяется (линия 3 на рис. 6). Очевидно, это связано с тем, что при таких давлениях газ не успевает охладиться в протяженной зоне, а среда нагревается нагнетаемым газом.
образуется область, в которой температура закачиваемого газа практически не изменяется (линия 3 на рис. 6). Очевидно, это связано с тем, что при таких давлениях газ не успевает охладиться в протяженной зоне, а среда нагревается нагнетаемым газом.
Для радиальной задачи система (7) перепишется в виде
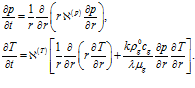 (15)
(15)
Решение радиальной задачи проведем, введя автомодельную переменную в виде 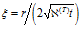 . Перейдем к автомодельным переменным:
. Перейдем к автомодельным переменным:
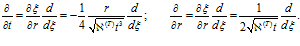
В итоге, после линеаризации уравнения пьезопроводности, система уравнений (15) примет вид

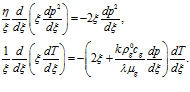 (16)
(16)
Произведем замены переменных: 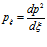 ,
, 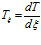 , тогда
, тогда
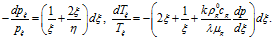 (17)
(17)
Распределение давлений получим, решая первое уравнение системы (17). Очевидно, что его решение имеет вид
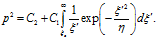 (18)
(18)
Из начальных и граничных условий
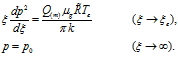
находим, что 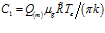 ,
, 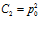 . Тогда (18) окончательно перепишется в виде
. Тогда (18) окончательно перепишется в виде
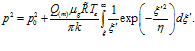 (19)
(19)
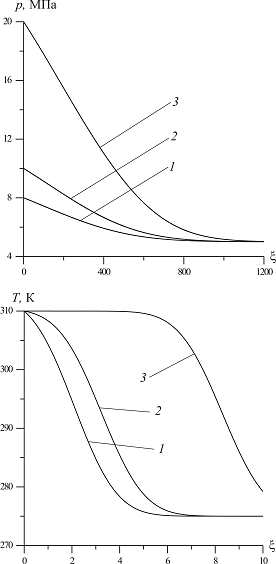
Рисунок 6. Демонстрация влияния давления закачиваемого газа на профили давлений и температур в пористой среде. Параметры среды: 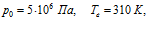
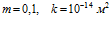 . Параметры закачиваемого газа:
. Параметры закачиваемого газа:
линии 1 – 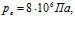 линии 2 –
линии 2 – 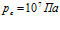 , линии 3 –
, линии 3 – 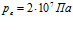 .
.
Рассмотрим второе уравнение системы (17). Проинтегрировав его, получим
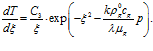
Отсюда:
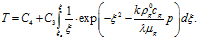 (20)
(20)
Так как
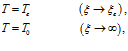
то 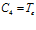 ,
, 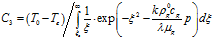 . В результате распределение температур в пористой среде принимает вид
. В результате распределение температур в пористой среде принимает вид
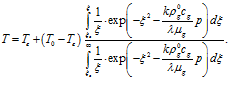 (21)
(21)
Результаты расчета для случая радиальной симметрии представлены на рис. 7 – 11.
На рис. 7
иллюстрируется влияние температуры закачиваемого газа на профили давлений и температур в среде при следующих значениях параметров: 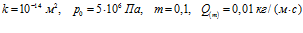 . Линии 1 соответствуют температуре закачиваемого газа
. Линии 1 соответствуют температуре закачиваемого газа 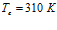 , линии 2 –
, линии 2 – 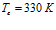 , линии 3 –
, линии 3 – 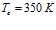 . Видно, что с ростом
. Видно, что с ростом 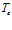 несколько расширяется зона перепада температур. Влияние температуры
несколько расширяется зона перепада температур. Влияние температуры 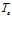 на профили давлений связано с тем, что при одном и том же массовом расходе газа более высокая температура
на профили давлений связано с тем, что при одном и том же массовом расходе газа более высокая температура 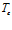 приводит к повышению давления на границе закачки, в результате чего давления вблизи границ скважины различаются.
приводит к повышению давления на границе закачки, в результате чего давления вблизи границ скважины различаются.
На рис. 8 проиллюстрировано влияние исходного пластового давления 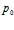 на профили давлений и температур в среде при следующих значениях параметров:
на профили давлений и температур в среде при следующих значениях параметров: 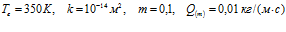 . Линии 1 соответствуют температуре закачиваемого газа
. Линии 1 соответствуют температуре закачиваемого газа 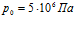 , линии 2 –
, линии 2 – 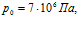 линии 3 –
линии 3 – 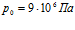 . Видно, что изменение давления
. Видно, что изменение давления 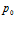 оказывает влияние лишь на профили давлений в пористой среде, но не влияет на распределение температур. Это связано с тем, что при одной и той же величине массового расхода
оказывает влияние лишь на профили давлений в пористой среде, но не влияет на распределение температур. Это связано с тем, что при одной и той же величине массового расхода 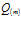 рост пластового давления ведет к росту давления на границе скважины.
рост пластового давления ведет к росту давления на границе скважины.
На рис. 9 показано распределение давлений и температур в среде при различных значениях проницаемости. Графики построены при следующих значениях параметров: 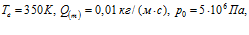
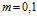 . Линии 1, 2 и 3 соответствуют проницаемостям
. Линии 1, 2 и 3 соответствуют проницаемостям 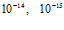 и
и 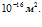 Распределения давлений в среде здесь объясняется ростом давления вблизи границы скважины при снижении проницаемости среды в условиях неизменного массового расхода
Распределения давлений в среде здесь объясняется ростом давления вблизи границы скважины при снижении проницаемости среды в условиях неизменного массового расхода 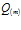 .
.
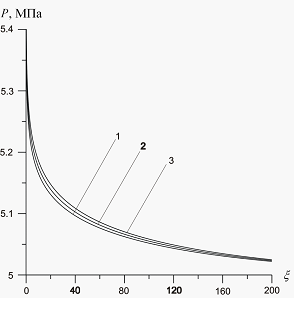
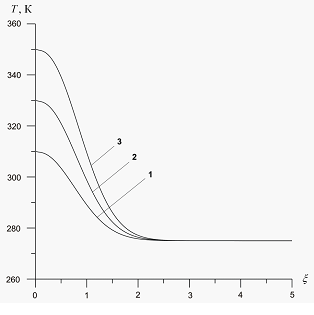
Рисунок 7. Влияние температуры закачиваемого газа на профили давлений и температур в пористой среде. Параметры среды: 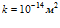 ,
, 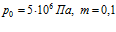 ,
, 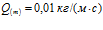 . Линии 1 –
. Линии 1 – 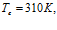 линии 2 –
линии 2 – 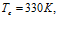 линии 3 –
линии 3 – 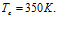
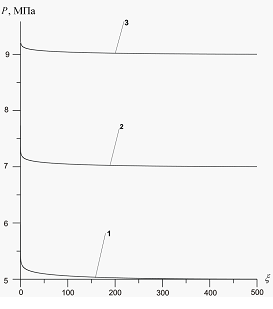
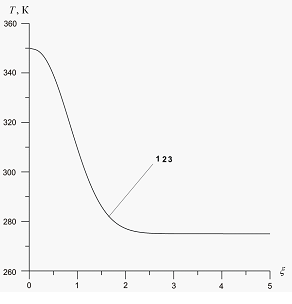
Рисунок 8. Влияние исходного пластового давления на профили давлений и температур в пористой среде. Параметры среды: 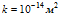 ,
, 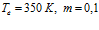 ,
, 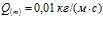 . Линии 1 –
. Линии 1 – 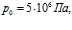 линии 2 –
линии 2 –  линии 3 –
линии 3 – 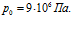
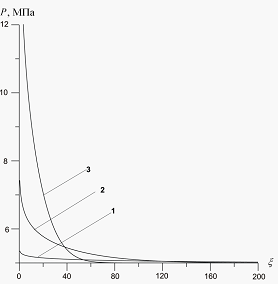
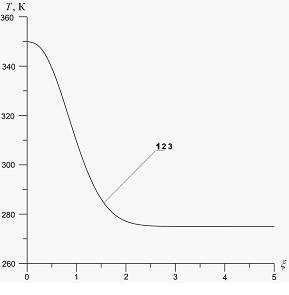
Рисунок 9. Влияние проницаемости среды на профили давлений и температур в пористой среде. Параметры среды: 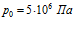 ,
, 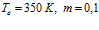 ,
, 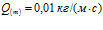 . Линии 1 –
. Линии 1 – 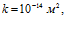 линии 2 –
линии 2 – 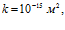 линии 3 –
линии 3 – 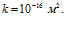
На рис. 10 показано влияние массового расхода газа на профили давлений и температур в среде при следующих значениях параметров: 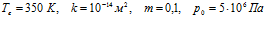 . Линии 1 соответствуют массовому расходу
. Линии 1 соответствуют массовому расходу 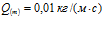 , линии 2 –
, линии 2 – 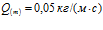 , линии 3 –
, линии 3 – 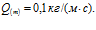 Видно, что с ростом массового расхода газа увеличивается давление вблизи границы скважины и увеличивается ширина зоны фильтрации; при этом наблюдается более глубокое проникновение температурной волны.
Видно, что с ростом массового расхода газа увеличивается давление вблизи границы скважины и увеличивается ширина зоны фильтрации; при этом наблюдается более глубокое проникновение температурной волны.
На рис. 11 показано влияние проницаемости на профили давлений и температур в среде при одинаковых значениях давлений вблизи границ скважины. Параметры среды и закачиваемого газа следующие: 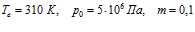 . Линии 1 построены при
. Линии 1 построены при 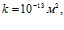
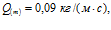 линии 2 –
линии 2 – 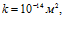
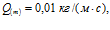 линии 3 –
линии 3 – 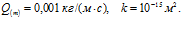 Необходимость разных массовых расходов связана с поддержанием одинаковых значений давлений вблизи границы скважины при изменении проницаемости среды. Видно, что в данных случаях уменьшение проницаемости среды ведет к сужению зон фильтрации и температурных перепадов.
Необходимость разных массовых расходов связана с поддержанием одинаковых значений давлений вблизи границы скважины при изменении проницаемости среды. Видно, что в данных случаях уменьшение проницаемости среды ведет к сужению зон фильтрации и температурных перепадов.
На основе проведенного исследования можно сформулировать следующие выводы.
Для плоскоодномерной задачи изменение исходного пластового давления оказывает влияние на распределения давлений и температур в среде. Так, с ростом 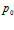 сужается зона фильтрации и отмечается более резкое падение температуры.
сужается зона фильтрации и отмечается более резкое падение температуры.
В случае радиальной задачи изменение температуры закачиваемого газа при постоянном массовом расходе оказывает влияние как на профили давлений, так и на профили температур. Отличия в профилях давлений связаны с тем, что с ростом температуры 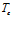 несколько повышается давление вблизи границ скважины (т.к. предполагается постоянство массового расхода газа).
несколько повышается давление вблизи границ скважины (т.к. предполагается постоянство массового расхода газа).
На профили давлений и температур в среде оказывают влияние и изменения других параметров: изменение проницаемости, давления 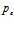 , массового расхода
, массового расхода 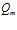 .
.
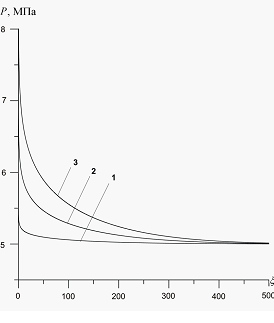
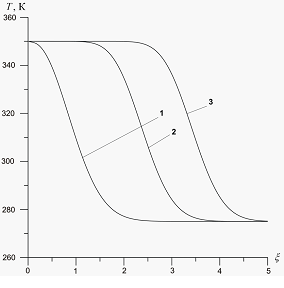
Рисунок 10. Влияние массового расхода закачиваемого газа на профили давлений и температур в пористой среде. Параметры среды: 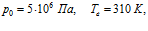
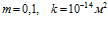 . Линии 1 –
. Линии 1 – 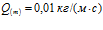 , линии 2 –
, линии 2 – 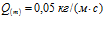 , линии 3 –
, линии 3 – 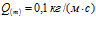 .
.
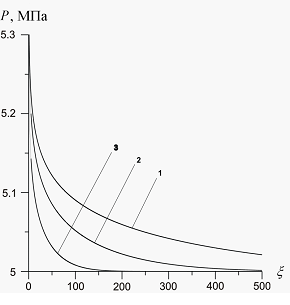
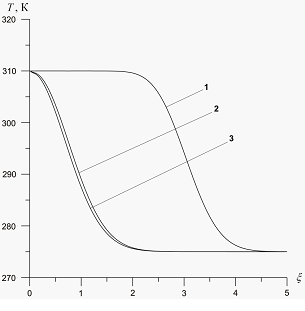
Рисунок 11. Демонстрация влияния проницаемости среды на профили давлений и температур в пористой среде при одинаковых значениях давлений вблизи границы скважины. Параметры среды: 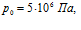
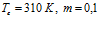 . Линии 1 –
. Линии 1 – 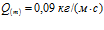 ,
, 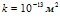 , линии 2 –
, линии 2 – 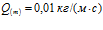 ,
, 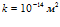 , линии 3 –
, линии 3 – 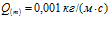 ,
, 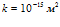 .
.
Библиографический список
- Дмитриев В.Л., Потапов А.А. Закачка в пласт горячего газа как энергоэффективный способ разработки газогидратного месторождения // ФИЗ-МАТ. 2013. № 4. – С. 3-12.
- Дмитриев В.Л., Потапов А.А. Инжекция горячего газа как энергоэффективный способ добычи газа из газогидратного месторождения // Сборник научных трудов II Всероссийской научно-технической конференции с международным участием «Высокие технологии в современной науке и технике». Т.2. – Томск: Изд-во Томского политехнического университета. 2013. – С. 365-368.
- Шагапов В.Ш., Насырова Л.А., Потапов А.А., Дмитриев В.Л. Тепловой удар под воздействием энергии излучения на пористую среду, частично заполненную газогидратом // Инженерно-физический журнал. 2003. Т.76. №5. – С. 47-53.
- Шагапов В.Ш., Рахматуллин И.Р., Насырова Л.А. К теории инжекции влажного пара в пористую среду // Теплофизика высоких температур. 2004. Т. 42. № 6. – С. 1-9.
