Уравнение Гаусса для расчета рассеивания загрязнения требует расчет параметра высоты факела выброса над уровнем земли (H_e). Он фактически складывается из высоты источника выброса H_s и увеличение шлейфа из-за движения воздушных масс Δh и описывается следующим уравнением:

H_e = H_s + Δh                                              (1)

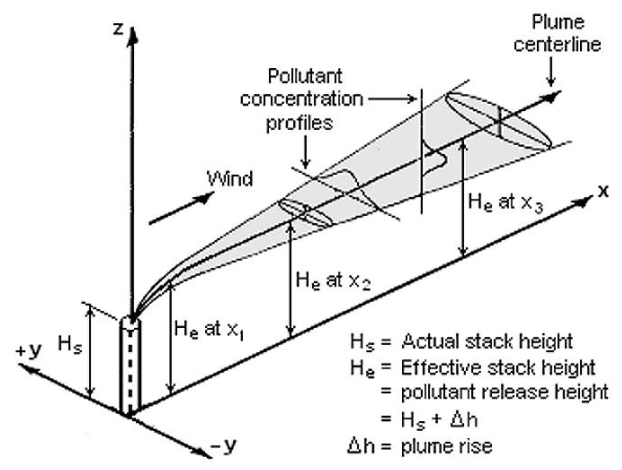
На рисунке 1 показано графическое описание уравнения (1)

Рисунок 1 – Визуализация сдвига шлейфа при распределении Гаусса [1]

Сдвиг шлейфа начиная с конца 60-х и до начала 2000-х определялся по уравнению Бриггса (1).

Бриггс впервые опубликовал свои наблюдения шлейфа в 1965 году [2]. После чего он сравнил многие высотные модели шлейфа доступные на тот момент CONCAWE [3] и в публикации под редакцией Слэйда [4].

В 1969 году, Бриггс предложил набор шлейфов высотных уравнений, которые стали широко известны как «уравнения Бриггса» [5]. Впоследствии он модифицировал их в 1971 году и в 1972 году [6,7].

Бриггс разделил особенности распределения шлейфом в 4 категории:

• Холодная струя шлейфа при штиле
• Холодная струя шлейфа в ветряных условиях
• Горячий перемешивающийся шлейф при штиле
• Горячий перемешивающийся шлейфов в ветряных условиях

Несмотря на то, что он предложил уравнение нарастания шлейфа для каждого из вышеперечисленных примеров, важно отметить, что уравнением, наиболее часто применяемым в расчетах, является уравнение горячих перемешивающихся шлейфов в ветряных условиях. Эти уравнения связываются с типичными источниками загрязнения как дымовые трубы, при сжигании топлива на крупных электростанциях, вносящих зачастую наибольших вклад в уровень загрязнения. Скорости выхода обычно в таких условиях достигают от 6 до 30 м/с и температурой от 120 до 260 °С.

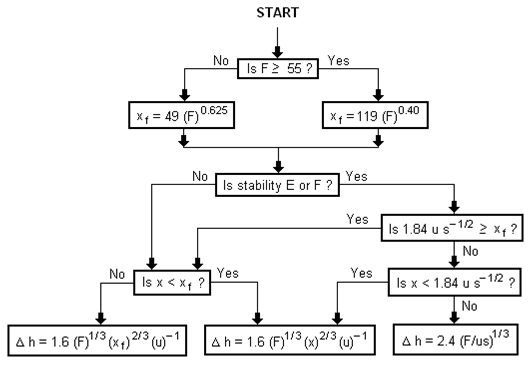
Перемешивающийся шлейф может быть рассчитан в соответствии с формулой Бриггса на основании логической диаграммы Бейчока представленной на рисунке 2.

Рисунок 2 – Логическая диаграмма использования шлейфов Бриггса [1]

где Δh повышение шлейфа, м;

F – фактор смешивания, м⁴с^-3;

x – расстояние от факела, до точки замера по направлению ветра, м;

x_f – расстояние от факела, до точки максимумы роста шлейфа;

u – скорость ветра на высоте фактического выброса м/с;

s – параметр стабильности, с^-2.

Применение шлейфов Бриггса в значительной степени способствует уточнению изначальных данных и, как следствие позволяет получить более адекватные модели.

1. Beychok, M. (2005). Fundamentals of Stack Gas Dispersion, Milton R. Beychok (Newport Beach, California).
2. Briggs, G.A. (1965). A plume rise model compared with observations. JAPCA, 15:433–438.
3. Briggs, G.A. (1968). Concawe meeting: Discussion of the comparative consequences of different plume rise formulas. Atmospheric Environment (1967), 2, 228-232.
4. Slade, D.H. (1968). METEOROLOGY AND ATOMIC ENERGY, 1968. Other Information: UNCL. Orig. Receipt Date: 31-DEC-68.
5. Briggs, G.A. (1969). Plume rise. USAEC Critical Review Series.
6. Briggs, G.A. (1971). Some recent analyses of plume rise observation. Proc. Second Internat’l. Clean Air Congress, Academic Press, New York.
7. Briggs, G.A. (1972). Chimney plumes in neutral and stable surroundings. Atmospheric Environment (1967), 6, 507-510.

Все статьи автора «Голубничий Артем Александрович»