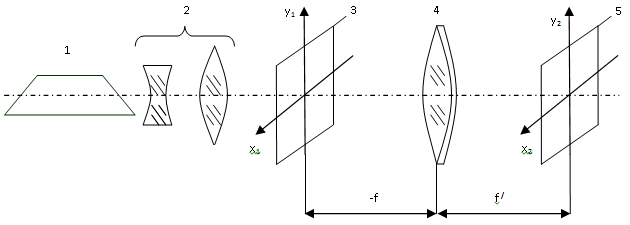
Оптическая система такого спектроанализатора выполнена по схеме «входной транспарант расположен за фурье – объективом» (рис. 1). В этой системе поток когерентного излучения лазера 1 расширяется телескопической системой 2 до размеров
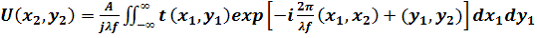 (1)
(1)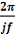
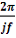 (
(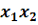
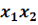 +
+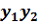
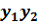 )],
)],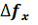 спектроанализатора будем поочерёдно помещать в плоскости 3 амплитудные спектральные решётки с коэффициентом пропускання
спектроанализатора будем поочерёдно помещать в плоскости 3 амплитудные спектральные решётки с коэффициентом пропускання
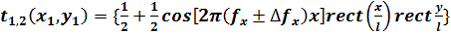 (2)
(2)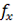 – пространственная частота, на которой определяется разрешающая способность; 2
– пространственная частота, на которой определяется разрешающая способность; 2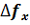 - пространственно – частотный интервал раздельного формирования максимумов спектра сигнала; rect – функция апертуры решёток, равная: 1 при
- пространственно – частотный интервал раздельного формирования максимумов спектра сигнала; rect – функция апертуры решёток, равная: 1 при 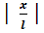 ≤
≤ 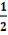
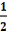 и 0 при
и 0 при 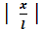 >
> 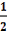
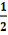 ; l - длина стороны апертуры решёток.
; l - длина стороны апертуры решёток.Подставив (2) в (1) и выполнив интегрирование, получим
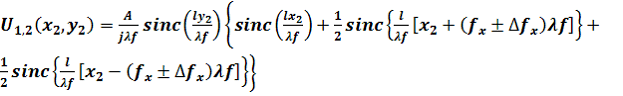 (3)
(3)Так как фотометрические устройства регистрации параметров спектра реагируют на освещённость Е, пропорциональную квадрату амплитуды U световой волны, то, возводя (3) в квадрат, получим
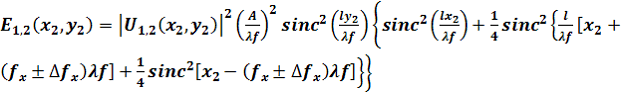 (4)
(4)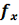 ±
±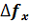 ) решётки много меньше размеров l её апертуры, двумя последними слагаемыми, содержащими произведение двух sinc- функций, можно пренебречь. Из оставшихся: первое слагаемое описывает спектр апертуры решётки с частотами
) решётки много меньше размеров l её апертуры, двумя последними слагаемыми, содержащими произведение двух sinc- функций, можно пренебречь. Из оставшихся: первое слагаемое описывает спектр апертуры решётки с частотами 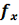 ±
±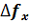 , второе и третье – спектр периодической структуры решётки с частотами
, второе и третье – спектр периодической структуры решётки с частотами 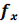 ±
±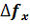 . Спектр периодической структуры решётки содержит два максимума, пространственное расстояние между которыми равно ±(
. Спектр периодической структуры решётки содержит два максимума, пространственное расстояние между которыми равно ±(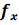 ±
±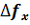 )λf, а ширина их пропорциональна λf/l.
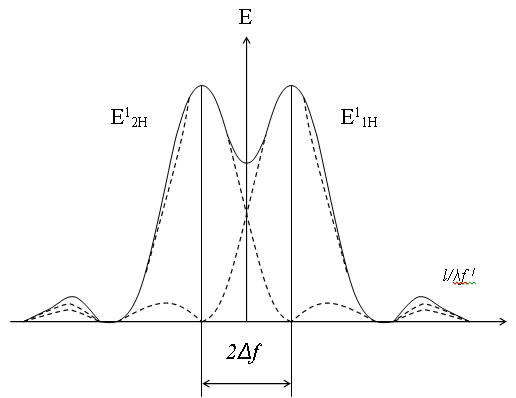
)λf, а ширина их пропорциональна λf/l.Нормированное распределение освещённости в этих максимумах для частот
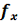 +
+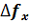 , показанное на рис 2, описывается выражениями
, показанное на рис 2, описывается выражениями
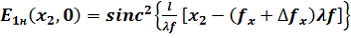 (5)
(5)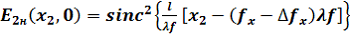 (6)
(6)Следуя критерию разрешения Реллея [ 3,4], уравнения (5) и (6) путём алгебраических преобразований можно свести к системе двух уравнений
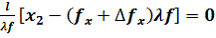 ,
,
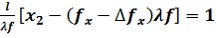 (7)
(7)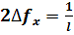 (8)
(8)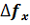 между максимумами спектра синусоидального сигнала, амплитуды которых формируются оптической системой спектроанализатора раздельно, ограничено размером l апертуры решётки, т.е. входного транспаранта 3. Как видно из (8), разрешающая способность
между максимумами спектра синусоидального сигнала, амплитуды которых формируются оптической системой спектроанализатора раздельно, ограничено размером l апертуры решётки, т.е. входного транспаранта 3. Как видно из (8), разрешающая способность 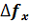 постоянна в плоскости 5 спектрального анализа и определяется лишь размером апертуры l входного транспаранта . Величина апертуры l транспаранта может быть легко и точно измерена обычной линейкой или штангенциркулем.
постоянна в плоскости 5 спектрального анализа и определяется лишь размером апертуры l входного транспаранта . Величина апертуры l транспаранта может быть легко и точно измерена обычной линейкой или штангенциркулем.Библиографический список
- Акаев А. А., Майоров С. А. Оптические методы обработки информации. – СПБ.: СПбГУ ИТМО, 2005. – 260 с.
- Назаров В.Н., Соколов Ю.А. Исследование схемы дифракционного контроля положений объектов с изменяющимся масштабом спектра Фурье // Научно-технический вестник СПбГУ ИТМО. – 2011. –№ 1 (71). – С. 6–9.