Введение. Кривошипно-ползунный механизм (КПМ) является наиболее распространенным механизмом, используемым в качестве главного исполнительного механизма большинства универсальных механических прессов, а также как механизм привода различных средств механизации технологических процессов. Вопросы синтеза и анализа таких механизмов рассмотрены в многочисленных трудах классиков теории механизмов. Однако использование КПМ как исполнительного механизма технологических машин, к которым относятся прессы и средства механизации, вносит ряд требований синтеза, вытекающих из технологического назначения машины. Недаром М.В. Семенов указывает, что синтез рычажных механизмов в общем случае является чрезвычайно сложной и еще не в полной мере решенной задачей [1]. В многочисленных работах рассматриваются вопросы синтеза указанного механизма по различным критериям синтеза, основными из которых являются условия существования механизма [1,2], условия достижения заданных положений ведомого звена [2], обеспечение заданных углов давления [3–4], синтез по заданному коэффициенту средней скорости [7–8], по условию постоянной скорости ползуна [9], по заданному передаточному отношению [10].
Цель работы. Целью настоящей статьи является обобщение теоретических сведений по синтезу кривошипно-ползунного механизма, а также решение некоторых задач синтеза при различных вариациях условий синтеза.
Материал и результаты исследований. Кривошипно-ползунный механизм, схема которого показана на рисунке, однозначно определен тремя геометрическими параметрами – радиус кривошипа R, длина шатуна L и смещение оси перемещения ползуна E, называемое эксцентриситет или дезаксиал. Принято считать эксцентриситет (дезаксиал) положительным, если он направлено в сторону вращения кривошипа в его нижнем положении и отрицательным, если он направлено против вращения кривошипа. Механизм характеризуется двумя относительными величинами:  – коэффициент шатуна;  – степень дезаксиала. Положение механизма однозначно определяется углом поворота кривошипа a, отсчитываемого от крайнего нижнего положения (кнп) против движения кривошипа и, соответствующим перемещением ползуна S, отсчитываемым также от кнп. Следовательно, синтез механизма состоит в определении указанных параметров, считающихся параметрами синтеза, удовлетворяющих заданным условиям синтеза. При трех параметрах механизма для однозначного его синтеза должно быть задано не менее трех условий синтеза. Во всех вариантах синтеза считаем заданной величину максимального перемещения ползуна S_m в совокупности с другими данными.
В соответствии с функциональным назначением механизма в структуре исполнительного органа механического пресса или средств механизации необходимо выполнение следующих требований:Ползун за один оборот главного вала (двойной ход) должен совершить перемещение между крайними верхним и нижним положением на заданную величину S_m. 
Параметры механизма должны удовлетворять условиям существования механизма при всех возможных положениях звеньев.
В зависимости от функционального назначения механизма на заданном интервале движения главного вала он должен обеспечить заданный закон перемещения ползуна.
Должны быть обеспечены наилучшие условий функционирования механизма, прежде всего, должны быть ограничены углы давления в кинематических парах.

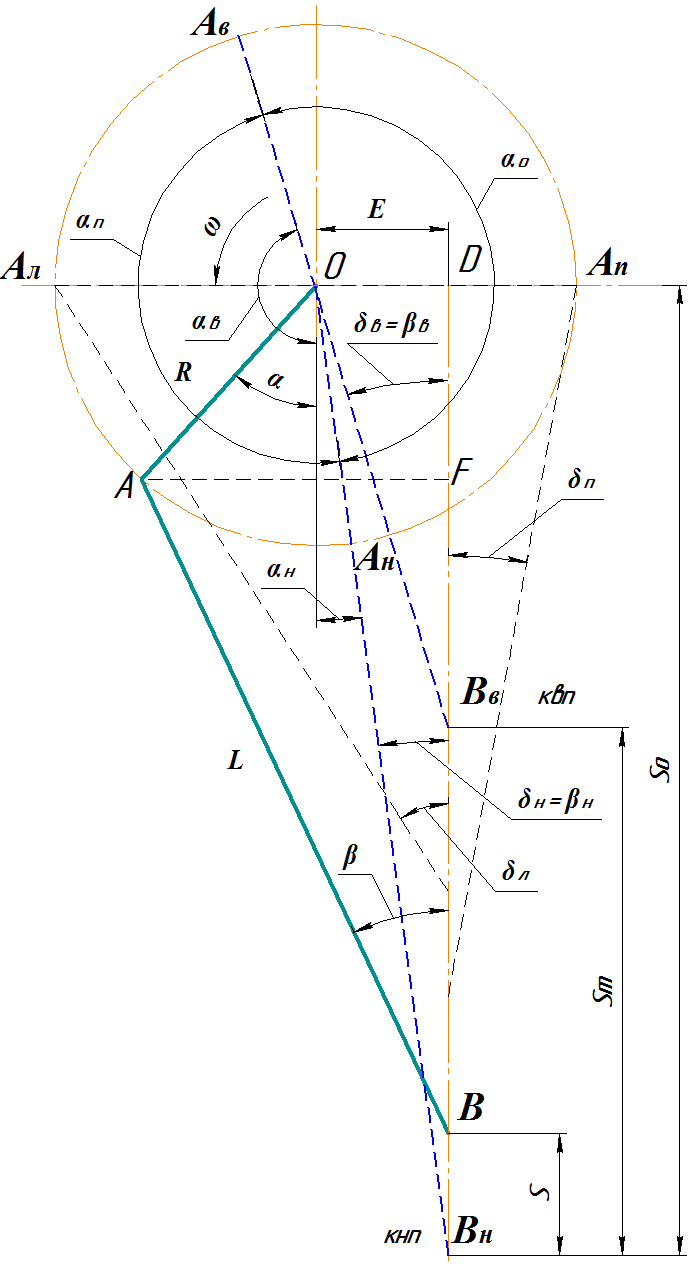
Схема кривошипно-ползунного механизма

Следовательно, критериями синтеза являются обеспечение заданного максимального перемещения ползуна S_m, обеспечение условия существования механизма, обеспечение заданных углов давления и обеспечение заданного коэффициента средней скорости. Условия синтеза представляются в виде сочетаний заданных параметров и ограничений.
Большинство задач синтеза кривошипно-ползунного механизма может быть решено в аналитическом виде.
Величина максимального перемещения ползуна определяется по формуле [1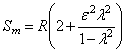1]

. (1)

Условие существования механизма представляется в виде , или в относительных единицах . Знак равенства соответствует предельному механизму, существование которого возможно, но функционирование невозможно вследствие недопустимых углов давления. По этой причине условия существования обычно записываются в виде

 и , (2)

где K_o – коэффициент ослабления, исключающий существование механизмов с недопустимыми углами давления. Принимается K_o = 0,85…0,9.
В рассматриваемом механизме угол давления в кинематической паре соединения шатуна с ползуном (точка В) есть угол Я, величина которого определяется по формуле

. (3)

Практический интерес представляют пять значений угла давления – в крайнем нижнем d_н и крайнем верхнем d_в положении кривошипа, в крайнем левом (при a = p/2) d_л и крайнем правом (при a = 3p/2) d_п положении кривошипа, а также в начале рабочего хода d_р (при a = a_р). Значения углов давления в крайних положениях определяются по формулам

, (4)
. (5)

Угол давления в начале рабочего хода определяется по формуле (3)

 (6)

при заданном угле начала рабочего хода (a = a_р), или положении ползуна в начале рабочего хода (S = S_нр). В последнем случае по формуле [11]

. (7)

определяется угол начала рабочего хода a_р, а затем находится угол давления d_р. Константы в этой формуле определяются как

.

Для аксиального механизма при Е = 0, зависимость (7) приводится к виду

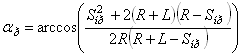. (8)

В крайнем левом или правом положениях кривошипа величина углов давления находится по формуле

, (9)

где верхний знак (плюс) принимается для левого положения кривошипа (a = p/2), а нижний (минус) – для правого положения.
Степень дезаксиала в расчетных формулах принимается с соответствующим знаком, потому при определенных условиях угол давления отрицательный, что свидетельствует о том, что шатун в расчетном положении отклоняется вправо от вертикальной линии перемещения ползуна.
В зависимости от функционального назначения механизма возможно несколько вариантов синтеза в зависимости от заданных условий синтеза. 
В настоящей работе рассмотрены вопросы синтеза кривошипно-ползунного механизма при различных вариантах сочетания заданных относительных параметров λ, e и заданных углах давления. Синтез механизма при заданном коэффициенте средней скорости K_v рассмотрен в следующей статье автора, представленной в настоящем сборнике.
1-й вариант. Задано: максимальное перемещение ползуна S_m, два параметра λ и e.
По формуле (1) определяется радиус кривошипа

, (10)

а затем определяются два других размера звеньев

. (11)

2-й вариант. Задано: максимальное перемещение ползуна S_m, радиус кривошипа R и параметр λ.
По формуле (1) определяется степень дезаксиала

, (12)

а затем по формулам (11) два линейных размера E и L . В формуле (12) имеется два корня, потому проектировщик должен определить тип механизма, т. е. знак дезаксиала.
3-й вариант. Задано: максимальное перемещение ползуна S_m, радиус кривошипа R и параметр e. Задача имеет решение при .
По формуле (1) определяется коэффициент шатуна

, (13)

а затем по формулам (11) два линейных размера R, E и L. Из двух значений коэффициента λ принимается положительное значение, т. к. второй корень невозможен.
В вариантах 2 и 3 должно соблюдаться условие , т. к. в противном случае механизм не существует.
4-й вариант. Задано: максимальное перемещение ползуна S_m, параметр λ, и максимальный угол давления d_max.
Угол давления будем иметь максимальное значение в зависимости от знака величины дезаксиала для крайнего левого положения кривошипа (при a = p/2, E > 0), или для крайнего правого положения кривошипа (при a = 3p/2, E < 0).
Из формулы (9) определяется величина степени дезаксиала

, (14)

а затем по формулам (10) и (11) три линейных размера R, E и L. В формуле (14) верхний знак принимается при проектировании механизма с положительным дезаксиалом, нижний – с отрицательным. В первом случае максимальным является угол d_л. Во втором случае E < 0, а максимальным является угол d_п.
5-й вариант. Задано: максимальное перемещение ползуна S_m, параметр e, и максимальный угол давления d_max.
Из формулы (9) определяется коэффициент шатуна

, (15)

а затем по формулам (10) и (11) три линейных размера R, E и L. Знак степени дезаксиала определяет какой из крайних углов является максимальным – левый d_л (E > 0), или правый d_п (при E < 0).
6-й вариант. Задано: максимальное перемещение ползуна S_m, параметр λ, и угол давления в начале рабочего хода d_р. Начало рабочего хода задано углом начала рабочего хода a_р.
По формуле (3) при  определяется степень дезаксиала

, (16)

а затем по формулам (10) и (11) три линейных размера R, E и L.
7-й вариант. Задано: максимальное перемещение ползуна S_m, параметр e, и угол давления в начале рабочего хода d_р. Начало рабочего хода задано углом начала рабочего хода a_р.
Задача аналогична задаче из предыдущего варианта. По формуле (3) при  определяется коэффициент шатуна

, (17)

а затем по формулам (10) и (11) три линейных размера R, E и L.
8-й вариант. Задано: максимальное перемещение ползуна S_m, параметр λ, и угол давления в начале рабочего хода d_р. Начало рабочего хода задано положением ползуна в начале рабочего хода S_р. Необходимо отметить, что этот вариант является достаточно распространенным при проектировании, как исполнительных механизмов прессов, так и средств механизации технологических процессов.
Точная зависимость перемещения ползуна от угла поворота кривошипа имеет вид [11]

. (18)

Из уравнения (3) следует . Используя приближенную зависимость

,

после подстановки в уравнение (18) совместно с уравнением (1) находим систему двух уравнений, из которых необходимо определить две неизвестные R и e при заданных S_р и λ

 (19)

Очевидно, что аналитическое решение системы невозможно, поэтому необходимо использовать один из численных методов решения системы нелинейных алгебраических уравнений. Как альтернативу можно рекомендовать следующий итерационный алгоритм для определения решения приближенным способом.
Полагается первое приближение неизвестной величины радиуса кривошипа и вычисляется первое приближение длины шатуна .
По формуле (7) определяется первое приближение угла начала рабочего хода a_р1.
По формуле (16) определяется первое приближение степени дезаксиала e₁.
Уточняется величина радиуса кривошипа R₂ по формуле (1) при заданном λ и первом приближенном значении e₁.
Уточняется величина длины шатуна  и производится возврат к шагу 2.
Для практических значений заданных исходных данных процесс сходится к конечным значениям R и e за 2–3 итерации с точностью до 5 знака.
Выводы
Критериями синтеза кривошипно-ползунного механизма являются обеспечение заданного максимального перемещения ползуна S_m, обеспечение условия существования механизма, обеспечение заданных углов давления и обеспечение заданного коэффициента средней скорости.
Большинство задач синтеза кривошипно-ползунного механизма может быть решено в аналитическом виде.
Представленные математические зависимости обеспечивают возможность синтеза механизма по любому варианту сочетания исходных данных и условий синтеза.

1.  Семенов М.В. Кинематические и динамические расчеты исполнительных механизмов / М.В. Семенов. – Л.: Машиностроение, 1974. – 432 с.
2. Артоболевский И.И. Теория машин и механизмов / И.И. Артоболевский. –М.: Наука, 1988. – 640 с.
3. Газаров А.Т. О нормах проектирования кривошипно-шатунных механизмов /А.Т. Газаров // Вестник машиностроения. – 1957, – № 3. С. 12–16.
4. Кольман-Иванов Э.Э. Применение номограмм при синтезе кривошипно-шатунных или приводящих к ним механизмов / Э.Э. Кольман-Иванов // Вестник машиностроения. – 1960, – № 12. С. 13–17.
5. Фараджев Т.Г. Синтез кривошипно-ползунного механизма / Т.Г. Фараджев, Ш.М. Багиров, А.И. Сухомлинов // Изв. вузов. Машиностроение. – 1977, – № 5. С. 47–50.
6. Дрягин Д.П. О нахождении передаточных функций и отношений скоростей точек в кривошипно-ползунных и коромыслово-ползунных механизмах / Д.П. Дрягин // Изв. вузов. Машиностроение. – 1986, – № 4. С. 41–44.
7. Белецкий В.Я. Проектирование кривошипно-шатунных механизмов по коэффициенту изменения скорости обратного хода и предельному углу передачи / В.Я. Белецкий // Изв. вузов. Машиностроение. – 1958, – № 3–4. С. 3–8.
8. Шебанов В.Т. Проектирование кривошипно-шатунных и кривошипно-коромысловых механизмов по коэффициенту изменения скорости хода / В.Т. Шебанов // Изв. вузов. Машиностроение. – 1958, – № 7–8. С. 36–47.
9. Белецкий В.Я. К синтезу кривошипно-шатунных механизмов с приближенно-постоянной скоростью рабочего звена / В.Я. Белецкий // Изв. вузов. Машиностроение. – 1958, – № 6. С. 10–14.
10. Карелин В.С. Проектирование кривошипно-ползунного механизма по заданному передаточному отношению. В.С. Карелин // Изв. вузов. Машиностроение. – 1982, – № 12. С. 35–38.
11. Явтушенко А.В. Кинематические характеристики дезаксиального кривошипно-ползунного механизма / А.В. Явтушенко, А.В. Глебенко, О.А. Калантева, А.С. Проскурня // Вісник Кременчуцького державного політехнічного університету ім. М. Остроградського. – Кременчук: КДТУ,– 2009. – Вип. 6/2009 (59, ч. 2). С. 94-99.

Все статьи автора «Явтушенко Александр Викторович»