Системы модального управления (СМУ) имеют широкие возможности в реализации высоких показателей качества протекания процессов: повышение быстродействия, устранение колебательности при наличии упругости и люфтов в кинематических связях. Поэтому вопросы оптимизации СМУ электроприводами становятся все более актуальными, им уделяется большое внимание [1].
В работе [2] описана математическая модель определения параметров модального регулятора желаемой формы, проведено исследование качественных показателей переходных режимов при управлении электродвигателем рольганга прокатного стана c традиционными структурами регуляторов систем подчиненного регулирования, оценены показатели эффективности применения модальных регуляторов в системах управления электрических приводов.
В рамках развития исследовательской работы [3] выполнен синтез модального регулятора (МР) для двухмассового электропривода с нежестким механическим звеном. Упругое звено с коэффициентом жесткости С12 связывает две массы: ротора и рабочего органа с моментами инерции J1и J2. В подобной системе при определенном соотношении параметров возможен незатухающий колебательный процесс изменения параметров режима электропривода. СМУ должна обеспечить заданные показатели в статике и динамике, устойчивость и стабилизацию движения.
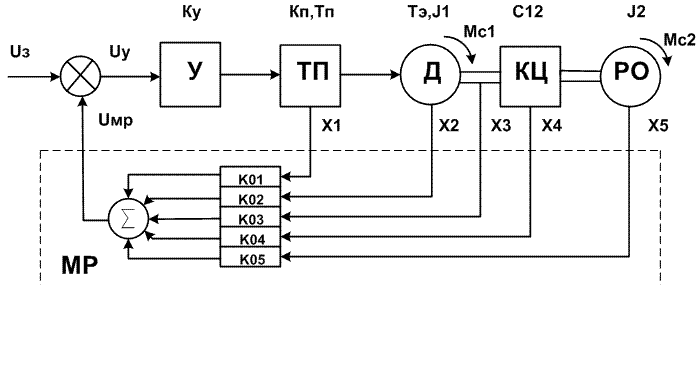
Функциональная схема двухмассовой электромеханической системы с МР приведена на рис.1.
Рисунок 1 – Функциональная схема двухмассовой ЭМС с МР
Основные элементы схемы:
- усилитель У с коэффициентом усиления Ку,
- тиристорный преобразователь ТП с ЭДС Еп ,коэффициентом усиления Кп и постоянной времени Тп,
- двигатель постоянного тока независимого возбуждения Д с коэффициентом передачи Кд, сопротивлением якорной цепи Rя, электромагнитной Tэ и электромеханической Тм постоянными времени, угловой скоростью ω и моментом трения Мс1,
- модальный регулятор с коэффициентами передачи входов Ко1 - Ко5,
- упругое звено кинематическая цепь (КЦ) с коэффициентом жесткости С12,
- рабочий орган РО с моментом инерции J2 и моментом сопротивления Мс2.
Напряжение управления Uy формируется сравнением напряжения задания Uз и напряжения модального регулятора Uр.
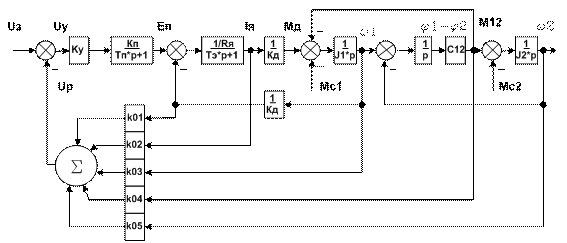
Структурная схема моделирования этой системы приведена на рис. 2.
Рисунок 2 – Структурная схема моделирования двухмассовой ЭМС с МР
Расчеты проведены для электропривода рольганга с нежесткой механикой широкополосного стана горячей прокатки мощностью 25 кВт, 1000 об/мин. Показатели качества переходных процессов подобных устройств определяют эффективность, производительность и надежность работы прокатного оборудования.
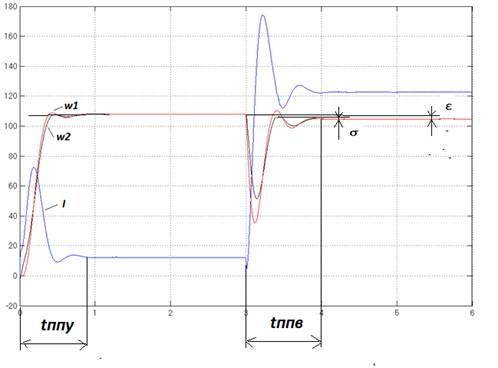
В программном пакете MATLAB проведено моделирование процесса управляемого пуска системы без нагрузки. В качестве возмущения рассмотрен скачок нагрузки до номинала через 3 с. Графики изменения основных параметров режима (тока якоря I и скоростей двух масс w1 и w2) при управлении и возмущении приведены на рис. 3.
Рисунок 3 – Графики изменения параметров режима системы с МР
Результаты анализа изменения основных параметров при управлении и возмущении (время переходного процесса tпп, перерегулирование σ, статическая ошибка ε и показатель колебательности М) сведем в таблицу 1.
Перерегулирование σ характеризует динамическую ошибку начала переходного процесса, а показатель колебательности М – количество полных колебаний до достижения установившегося режима.
Таблица 1 – Основные показатели качества регулирования
|
Параметр |
Система |
При управлении | При возмущении | ||||||
| tпп,с | σ,% | ε,% | M | tпп,с | σ,% | ε,% | M | ||
|
Ток якоря |
САУ с МР |
0,7 | 45 | 0 | 1,5 | 0,8 | 25 | 0 | 1,5 |
|
Скорость w2 |
САУ с МР |
0,7 | 0 | 0 | 0,5 | 0,8 | 5 | 5 | 1,5 |
Анализ параметров и их сравнение с результатами исследования систем подчиненного регулирования [2,3] показывает, что САУ ЭМС с модальным управлением позволяет существенно улучшить показатели качества переходных процессов: повысить быстродействие и устранить колебательность.
Выводы:
1. Разработана математическая модель системы управления двухмассовой электромеханической системы с использованием модального регулятора желаемой эталонной формы на примере электропривода рольганга широкополосного листового прокатного стана.
2. Проведено исследование показателей качества переходных процессов САУ нелинейной двухмассовой ЭМС с модальным регулятором.
3. Показана высокая эффективность использования модального управления электроприводами в металлургических агрегатах с нежесткой механикой .
Библиографический список
- Синтез систем автоматического управления методом модального управления. В.В. Григорьев, Н.В. Журавлёва, Г.В. Лукьянова и др. – С-Пб: СПбГУ ИТМО, 2007. – 108 с.
- Кочнева Т.Н., Кожевников А.В., Кочнев Н.В. Модальное управление электромеханическими системами в металлургии // Вестник Череповецкого государственного университета. Научный журнал. – Череповец: ФБГОУ ВПО ЧГУ. – № 1 (45). Т.1 – 2013. – С. 11-16.
- Кочнева Т.Н., Кожевников А.В., Кочнев Н.В. Синтез модального регулятора и оценка эффективности модального управления для двухмассовых электромеханических систем // Вестник Череповецкого государственного университета. Научный журнал. – Череповец: ФБГОУ ВПО ЧГУ. – № 4 (52). Т.2 – 2013. – С. 15-22.