Введение. Для точных деталей типа «тело вращения» является актуальной задача определения параметров точности формы (отклонение от круглости, отклонение от цилиндричности) и взаимного расположения (отклонение от соосности, отклонение от перпендикулярности), а также радиального и торцового биений.
Численные значения отклонений от круглости сечений деталей типа «тело вращения» определяются с помощью кругломеров, либо с помощью координатно-измерительных машин (КИМ). Нередко отклонение от круглости измеряют без кругломера и КИМ по 2-3 точкам («эллипс», «огранка»), но методическая составляющая погрешности в данном случае зачастую превышает общую допустимую погрешность измерения отклонения от круглости [1, 2].
В настоящее время практически на всех машиностроительных предприятиях и в высших учебных заведениях отклонение от круглости определяется согласно ГОСТ 24642-81 [3], несмотря на то, что данный ГОСТ был отменен 1 января 2012 г. введением ряда ГОСТ, включая ГОСТ Р 53442-2009 [4]. В данной статье предлагаются к рассмотрению блок-схемы, реализующие оба государственных стандарта.
Цель. Необходимо описать алгоритмы определения численных значений отклонений от круглости согласно двум принятым на территории РФ методикам в виде блок-схем.
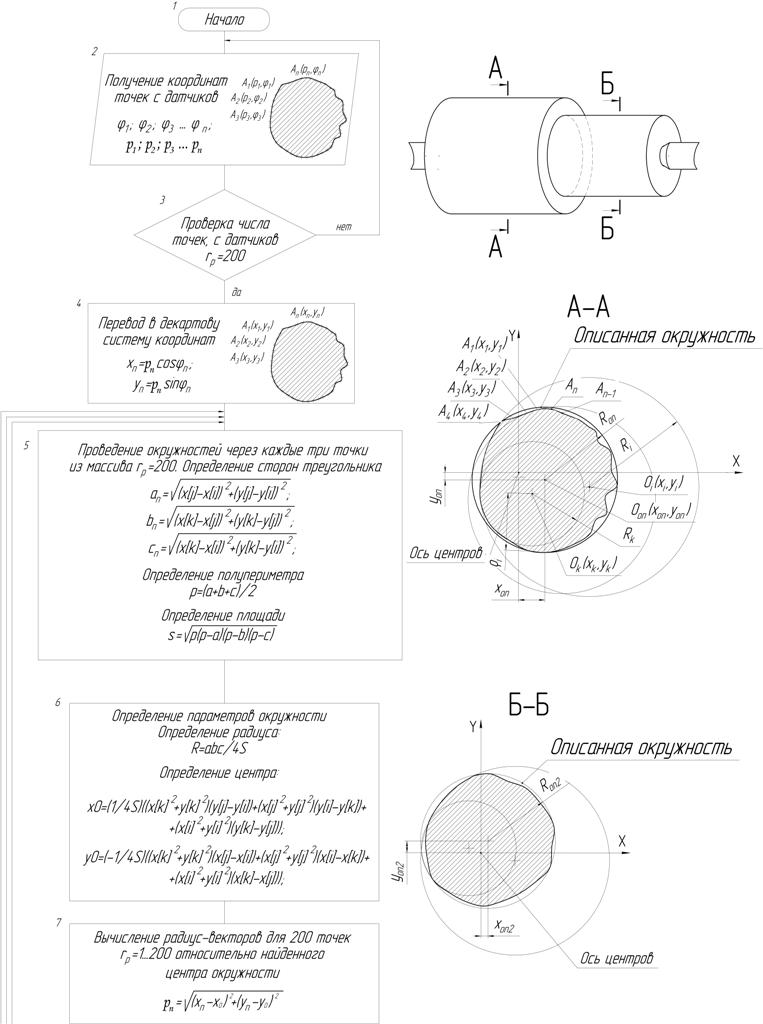
Блок-схема определения отклонения от круглости согласно ГОСТ 24642-81. В блок-схеме реализуется следующая методика определения отклонения от круглости:
- Рассматривается деталь «тело вращения», закрепленная в центрах; для измеряемой детали выбираются срединные сечения контролируемых цилиндрических поверхностей (рис. 1, А-А, Б-Б);
- Для выбранного сечения А-А каким-либо способом, например – с помощью датчика перемещения, определяются координаты множеств точек контура сечения (см. рис. 1, блок 2). Количество точек сечения зависит от эксплуатационных характеристик шагового двигателя, согласно авторским исследованиям, необходимое количество точек при ожидаемой методической составляющей погрешности порядка 0,001 мм составляет 150-200 точек (блок 3). Координаты могут быть сохранены в декартовых, либо полярных координатах. Координаты определяются в полярных координатах (угол поворота — тарированный, зависит от шагового двигателя, радиус вектор точек сечения равен начальному радиус-вектору с дальнейшим прибавлением/вычитанием приращений, определяемых датчиком перемещения), далее в ходе программной обработки данных и поиска параметров точности, в данном случае — отклонения от круглости, полярные координаты переводятся в декартовы (блок 4);
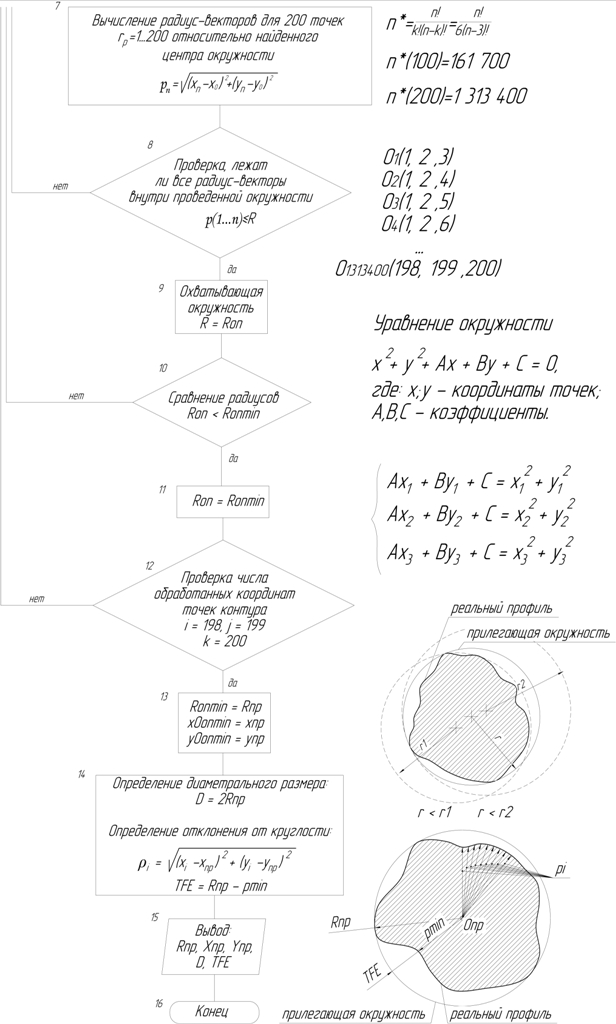
- На выбранном сечении через каждые три точки проводятся окружности, после чего проверяется, являются ли эти окружности охватывающими, т.е. не лежат ли точки сечения за пределами полученной окружности (если хотя бы одна из точек сечения лежит за пределами окружности, такая окружность не может являться охватывающей и в дальнейших расчетах не участвует, см. рис. 1, 2, блоки 5, 6, 7, 8, 9). Математические формулы, используемые для нахождения окружностей и их параметров представлены в блоках 5, 6. Для определения относительного местоположения точки сечения (внутри/снаружи) вычисляются радиус-векторы от центра сечения до точки контура (блок 7). Для того чтобы выполнялось условие описанной окружности относительно измеряемого сечения, необходимо, чтобы все радиус-векторы от центра окружности до точек контролируемого сечения были меньше либо равны радиусу рассматриваемой окружности (блок 8). При количестве исследуемых точек = 200 штук, количество перебираемых окружностей = 1 313 400 штук;
- После перебора всех точек этого сечения (по три), выбирается наименьший диаметр охватывающей окружности, эта окружность будет являться прилегающей (описанной) для выбранного сечения (см. рис. 2, блоки 9, 10, 11);
- Параметры (центр и радиус) найденной окружности запоминаются (см. рис. 2, блок 11). Описанный набор действий осуществляется для всех исследуемых точек сечений (200, см. рис. 2), блок 12;
- Удвоенный радиус прилегающей (наименьшей из охватывающих, блок 13) окружности будет являться диаметральным размером детали в измеряемом сечении (цель определения диаметра в данной методике не преследуется, тем не менее, он получается автоматически при вычислении отклонения от круглости, см. рис. 2, блок 14);
- Для измеряемого сечения осуществляется пересчет радиус-векторов измеренных точек контура относительно найденного в п.5 центра прилегающей окружности (см. рис. 2, блок 14);
- Для каждой точки контура сечения измеряемой цилиндрической поверхности определяется отклонение радиуса прилегающей окружности от пересчитанных радиус-векторов точек, найденных в п.7 (см. рис. 2, блок 14);
- Максимальное из этих отклонений будет являться отклонением от круглости [1, 2, 3] (см. рис. 2, блок 14 [3]);
- Для сечения Б-Б и любых других повторяются пп. 2–9 методики (см. рис. 1, 2) [1, 2, 3].
Рис. 1. Блок-схема для определения отклонения от круглости. Часть 1.
Рис. 2. Блок-схема для определения отклонения от круглости. Часть 2.
Данная блок-схема позволяет определять отклонение от круглости сечений цилиндрических поверхностей деталей в соответствии с ГОСТ 24642-81 с методической погрешностью, не превышающей 1 мкм для сечений деталей до 100 мм.
Данные о прилегающей окружности позволяют также с высокой точностью вычислять отклонение от соосности и радиальное биение в сечениях измеряемых деталей, данные о прилегающей плоскости, определяемой по подобной методике позволяют определять отклонение от перпендикулярности, параллельности, плоскостности, торцовое биение [1, 2, 5, 6, 7, 8, 9].
При увеличении диаметров сечений (свыше 100 мм), либо при необходимости точности измерений свыше 1 мкм количество исследуемых точек сечений следует увеличить (свыше 200).
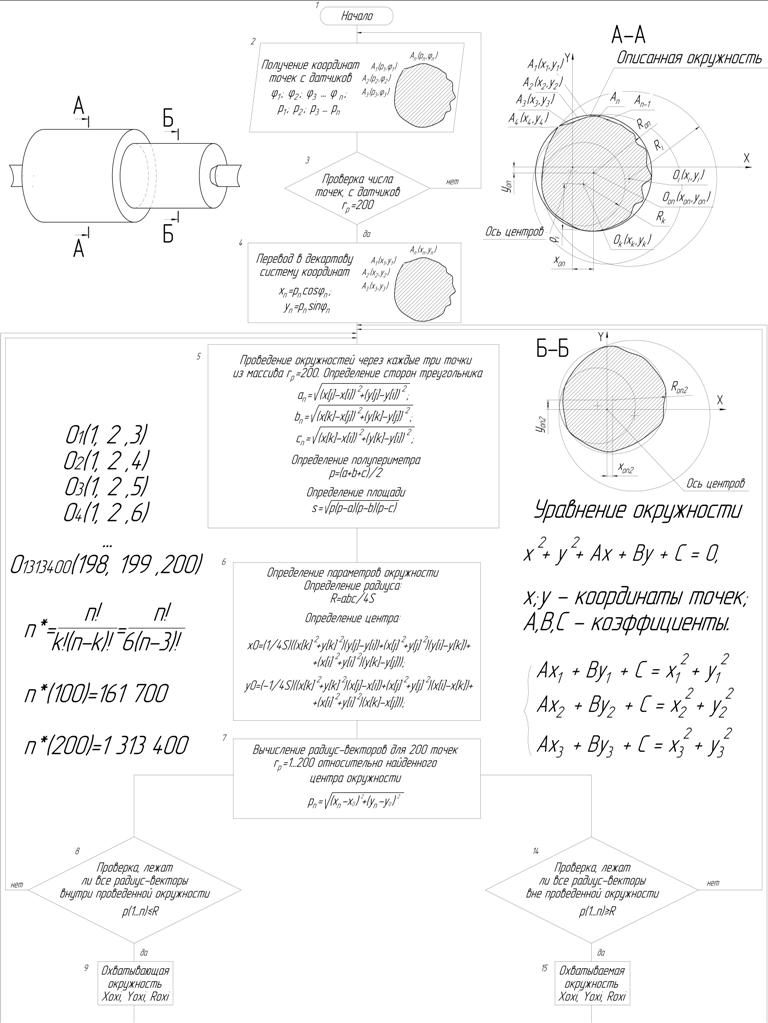
Блок-схема определения отклонения от круглости согласно ГОСТ Р 53442-2009. В данном ГОСТ отклонение от круглости определяется без использования понятия прилегающей окружности. «Считается, что круглость отдельного элемента, для которого устанавливается допуск, определена корректно, если элемент располагается между двумя концентрическими окружностями, разность радиусов которых не более значения установленного допуска. Положение центров этих окружностей и значения их радиусов должны выбираться так, чтобы разность радиусов двух концентрических окружностей равнялась возможному наименьшему значению» [4].
- Рассматривается деталь «тело вращения», закрепленная в центрах; для измеряемой детали выбираются срединные сечения контролируемых цилиндрических поверхностей (рис. 3, А-А, Б-Б);
- Для выбранного сечения А-А каким-либо способом, например – с помощью датчика перемещения, определяются координаты множеств точек контура сечения (см. рис. 3, блок 2). Количество точек сечения зависит от эксплуатационных характеристик шагового двигателя, согласно авторским исследованиям, необходимое количество точек при ожидаемой методической составляющей погрешности порядка 0,001 мм составляет 150-200 точек (блок 3). Координаты могут быть сохранены в декартовых, либо полярных координатах. Координаты определяются в полярных координатах (угол поворота — тарированный, зависит от шагового двигателя, радиус вектор точек сечения равен начальному радиус-вектору с дальнейшим прибавлением/вычитанием приращений, определяемых датчиком перемещения), далее в ходе программной обработки данных и поиска параметров точности, в данном случае — отклонения от круглости, полярные координаты переводятся в декартовы (блок 4);
- На выбранном сечении через каждые три точки проводятся окружности, после чего проверяется, являются ли эти окружности охватывающими, т.е. не лежат ли точки сечения за пределами полученной окружности (если хотя бы одна из точек сечения лежит за пределами окружности, такая окружность не может являться охватывающей и в дальнейших расчетах не участвует, см. рис. 3, блоки 5, 6, 7, 8, 9). Математические формулы, используемые для нахождения окружностей и их параметров представлены в блоках 5, 6. Для определения относительного местоположения точки сечения (внутри/снаружи) вычисляются радиус-векторы от центра сечения до точки контура (блок 7). Для того чтобы выполнялось условие описанной окружности относительно измеряемого сечения, необходимо, чтобы все радиус-векторы от центра окружности до точек контролируемого сечения были меньше либо равны радиусу рассматриваемой окружности (блок 8). При количестве исследуемых точек = 200 штук, количество перебираемых окружностей = 1 313 400 штук;
- После перебора всех точек этого сечения (по три), находятся все охватывающие окружности (а не одна, минимальная, как в предыдущей методике, см. рис. 3, блок 9);
- Параметры (центр и радиус) найденных окружностей запоминаются;
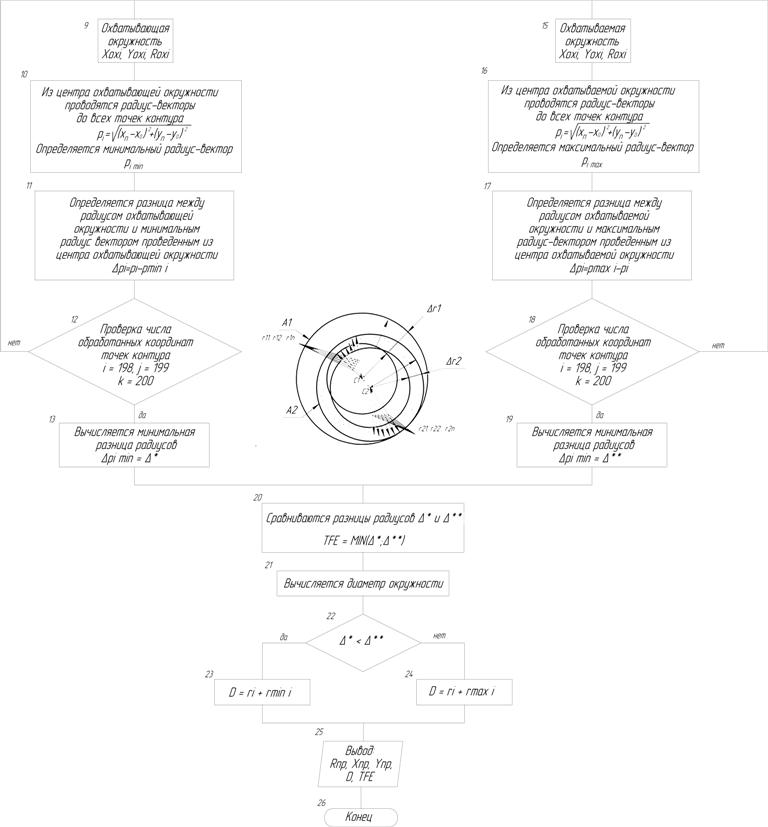
- Из центра охватывающей окружности 1 (см. рис. 4, блок 10) проводятся радиус-векторы до всех точек контура (r11, r12…r1n);
- Определяется минимальный радиус-вектор, после чего с данным радиусом из центра охватывающей окружности проводится окружность (охватываемая), что реализует схему, (см. рис. 4) [4];
- Разница радиусов охватывающей и охватываемой окружностей (Δr1) запоминается (см. рис. 4, блок 11);
- Далее пп. 6-8 повторяются для всех охватывающих окружностей, найденных в пп.3-5;
- Разницы радиусов Δr1, Δr2… Δrn сравниваются, минимальная разница радиусов Δr* запоминается (см. рис. 4, блок 13);
- На выбранном сечении через каждые три точки проводятся окружности, после чего проверяется, являются ли они охватываемыми, т.е. не лежат ли точки сечения внутри проведенной окружности, если хотя бы одна из точек сечения находится внутри (радиус-вектор меньше радиуса), такая окружность отбрасывается и в дальнейших расчетах не участвует (см. рис. 4, блоки 14, 15);
- После перебора всех точек этого сечения (по три), находятся все охватываемые окружности;
- Параметры (центр и радиус) найденных окружностей запоминаются;
- Из центра первой охватываемой окружности проводятся радиус-векторы до всех точек контура (см. рис. 4, блок 16);
- Определяется максимальный радиус-вектор, с данным радиусом из центра охватываемой окружности проводится окружность (охватывающая, см. рис. 4, блок 16);
- Разница радиусов охватывающей и охватываемой окружностей запоминается (см. рис. 4, блок 17);
- Далее пп. 14-16 повторяются для всех охватываемых окружностей, найденных в пп.11-13;
- Минимальная разница радиусов Δr** запоминается (см. рис. 4, блок 19);
- Сравниваются разницы радиусов из п.10 и п.18, минимальная из них является искомой «круглостью» или отклонением от круглости (см. рис. 4, блок 20);
- Далее, вычисляется диаметр контролируемого сечения как средний между окружностями с разницей радиусов (MIN(Δr*; Δr**) из п. 19, см. блоки 21-24) [1, 2, 4, 5, 6, 9].
- Определяется максимальный радиус-вектор, с данным радиусом из центра охватываемой окружности проводится окружность (охватывающая, см. рис. 4, блок 16);
- Разница радиусов охватывающей и охватываемой окружностей запоминается (см. рис. 4, блок 17);
- Далее пп. 14-16 повторяются для всех охватываемых окружностей, найденных в пп.11-13;
- Минимальная разница радиусов Δr** запоминается (см. рис. 4, блок 19);
- Сравниваются разницы радиусов из п.10 и п.18, минимальная из них является искомой «круглостью» или отклонением от круглости (см. рис. 4, блок 20);
- Далее, вычисляется диаметр контролируемого сечения как средний между окружностями с разницей радиусов (MIN(Δr*; Δr**) из п. 19, см. блоки 21-24) [1, 2, 4, 5, 6, 9].
Рис. 3. Блок-схема 2 для определения отклонения от круглости. Часть 1.
Рис. 4. Блок-схема 2 для определения отклонения от круглости. Часть 2.
Выводы. Блок-схемы, представленные в статье, позволяют определять отклонение от круглости: 1) согласно ГОСТ 24642-81 [3], формально отмененному, но фактически применяемому практически на всех машиностроительных предприятиях и ВУЗ России; 2) согласно ГОСТ Р 53442-2009, введенному 01.01.2012 г [4]. Область применения. Данная статья и материалы, в ней представленные, могут быть полезны сотрудникам высших технических учебных заведений, а также работникам технологических, метрологических и других служб машиностроительных предприятий, имеющим отношение к вычислению параметров точности формы и взаимного расположения поверхностей деталей в понимании и решении задачи определения численных значений отклонений от круглости [1, 2, 5, 6, 7, 8, 9].
Библиографический список
- Высогорец Я.В., Чемборисов Н.А. Методика контроля групп параметров точности цилиндрических и торцевых поверхностей деталей // Вестник ИрГТУ №12 (59), 2011. – С.20-26.
- Высогорец, Я.В. Экспериментальные исследования методик контроля параметров точности цилиндрических и торцевых поверхностей деталей / Я.В.Высогорец. // Вестник ИрГТУ №09 (68), 2012 (ISSN 1814-3520). – С.23-29.
- ГОСТ 24642-81. Основные нормы взаимозаменяемости. Допуски формы и расположения поверхностей. Основные термины и определения. Изд. офиц. – Частично взамен ГОСТ 10356-63. – Введ. с 1981-07-01. – М.: Изд-во стандартов, 1981. – 111 с.
- ГОСТ Р 53442-2009 (ИСО 1101:2004). Основные нормы взаимозаменяемости. Характеристики изделий геометрические. Допуски формы, ориентации, месторасположения и биения. – Введен впервые; Введ. 01.01.2012. – 51 с.
- Высогорец, Я.В. Автоматизированный контроль и прецизионная обработка цилиндрических и торцевых поверхностей / Я.В. Высогорец, В.М. Лопатин, С.Г. Чиненов // Прогрессивные технологии и системы машиностроения. – Донецк: ДонНТУ, 2011 (ISSN 2073-3216). – С.72-79.
- Высогорец Я.В. Исследование операций контроля цилиндрических и торцевых поверхностей деталей / Я.В. Высогорец, Н.А. Чемборисов, А.Н. Саубанов // Прогрессивные технологии и системы машиностроения. Международный сборник научных трудов №1 (47), 2014. – Донецк: ДонНТУ, 2014 (ISSN 2073-3216). – С.79-84.
- Пат. 2 348 006 C1 Российская Федерация, МПК51 G01В 5/08, G 01 B5/12. Способ размерного контроля поверхностей деталей, имеющих круглые сечения / С.Г. Чиненов, С.П. Максимов, Я.В. Высогорец. – № 2007126311/28; заявл. 10.07.07; опубл. 27.02.09, Бюл. № 6 – 15 с.
- Свидетельство о государственной регистрации программы для ЭВМ № 2011614778. Программа для определения параметров точности цилиндрических поверхностей деталей типа «тело вращения» / Я.В. Высогорец, С.Г. Чиненов; заявка № 2011613133 от 29.04.2011. – 26 с.
- Чиненов С.Г. Математическое моделирование операций комплексного размерного контроля деталей машин. / С.Г.Чиненов, Я.В.Высогорец, С.П.Максимов // Вестник ИрГТУ №8 (55), 2011 (ISSN 1814-3520). – С.172-176.