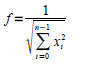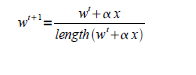Для обучения нейронной сети распознавать цифры от 0 до 9 используется сеть с упорядоченными нейронами или самоорганизующаяся карта. Изначально на вход поступают входные нейроны. Самоорганизующаяся карта накладывает условие, что входной массив нейронов должен быть нормализован и должен лежать в пределах -1 и 1 [1]. В случае с самоорганизующейся картой только один из нейронов принимает значение true или false.
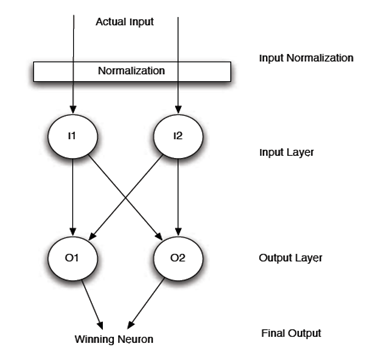
Структура такой сети приведена на рисунке 1.
Рисунок 1. Структура самоорганизующейся карты
Самоорганизующаяся карта требует, чтобы входной поток нейронов был нормализован в пределах от -1 до 1. Причем каждый из входных нейронов должен полностью использовать этот диапазон. Если бы один или два нейрона использовали только числа между 0 и 1, то нейронная сеть бы пострадала.
Есть два основных способа нормализации данных:
1) Мультипликативная нормализация.
2) Z-нормализация.
На практике следует применять оба метода. Первый способ довольно прост. Но второй способ обеспечивает лучшее распределение значений внутри диапазона.
Для того, чтобы выполнить нормализацию, нужно вычислить длину вектора входных данных. Фактор нормализации рассчитывается по формуле:
Для второго способа формула выглядит иначе:
Равенство показывает, что фактор нормализации зависит только от размера исходных данных. Таким образом, эта величина всегда постоянно и не позволяет учитывать фактические данные. Чтобы это учесть, вводят синтетический показатель, который также рассчитывается по формуле [2]:
где n- это размер входных данных, f – фактор нормализации, а l – это длина вектора
Второй метод на практике используют чаще, так как он позволяет сохранять абсолютную величину. Но если обучающие значения будут около нуля, то такой подход не самый лучший, так как синтетический фактор будет преобладать над другими ненулевыми значениями. В этом случае, следует применять первый метод.
Чтобы вычислить выходной нейрон, используется входной вектор и нейронные веса связей. Должно быть вычислено скалярное произведение между вектором входных нейронов и вектором их весов связей. Соответственно, чтобы вычислить такое скалярное произведение, нужно преобразовать каждый элемент в вектор. Данные вычисления применяются для каждого нейрона в отдельности. Получившееся скалярное произведение умножается на фактор нормализации. Полученный результат должен быть нормализован с учетом биополярной системой.
Биополярное число – это альтернативный способ представления бинарных чисел. В биополярной системе бинарный ноль преобразуется в -1, а бинарная единица в 1. Поэтому все значения выходных нейронов преобразуются в эту систему.
Чтобы определить нейрона победителя, нужно для каждого нейрона в отдельности выполнить вышеуказанные вычисления и нормализовать значения. Далее тот нейрон, у которого выходное значение больше, является победителем.
В целом, процесс обучения такой сети состоит из нескольких шагов или итераций и повторяется до тех пор, пока ошибка сети будет ниже заданного порога. Кроме того, нужно рассчитывать на каждом шаге коэффициент ошибок сети и корректировать веса нейронов.
Сам процесс обучения основан на конкуренции между нейронами. Это означает, что только один нейрон выигрывает. Так как разные нейроны на разных итерациях выигрывают для разных моделей, то их способность распознавания увеличивается. Процесс обучения повторяется до тех пор, пока не выполнится одно из двух условий. Если вычислительная ошибка станет ниже порога, то обучение завершается. И если коэффициент ошибки изменится на очень маленькое число, то цикл будет прерван без каких-либо дополнительных повторений. Как только цикл прерывается, обучение начинается заново и веса на начальном этапе для нейронов генерируются случайно [1].
Коэффициент обучения или скорость обучения должна быть положительным числом и меньше чем 1. Типично берут значение в диапазоне от 0.4 до 0.5. Если резко увеличивать скорость обучения, то процесс обучения будет быстрый. Но сеть может расходиться на последних итерациях в результате такой высокой скорости. Это может произойти в результате того, что погрешности весов будут слишком велики для процесса распознавания образов.
Поэтому лучше всего установить на начальных итерациях высокую скорость и снижать ее постепенно. Это позволит увеличить первоначальную скорость обучения и сохранить сеть.
В процессе обучения также осуществляется регулирование весов нейронов. Веса регулируются на каждой итерации. Для расчёта весов используется метод Кохонена:
x- вектор обучения; wt – длина нейрона-победителя; wt+1 – новый вес.
При решении задачи были реализованы основные классы:
1) класс Matrix и MatrixMath, который содержит методы для работы с матрицей и преобразования векторов;
2) Normalize – реализует методы нормализации входных нейронов;
3) SelfOrganizingMap – реализует самоорганизующуюся сеть;
4) TrainSelfOrganizingMap – реализует процесс обучения сети.
Идея программы заключается в том, что пользователь рисует какой-то символ, и у него есть несколько сценариев:
1) обучить сеть нарисованным буквам;
2) распознать нарисованный символ;
3) загрузить из файла заранее заданные символы для обучения.
Перед процессом распознавания образов необходимо нарисованное изображение преобразовать к матрице размером 5х7. Кроме того, необходимо обрезать изображение, и удалить все пустые белые пространства.
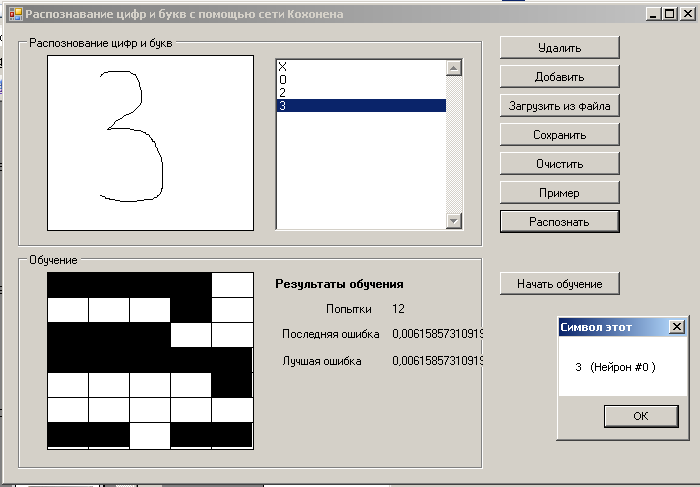
Результат работы обученной нейронной сети приведен на рисунке 2.
Рисунок 2. Результаты обучения нейронной сети
Программа позволяет методом Кохонена вычислять текущую и лучшую ошибку обучения нейронной сети. Следует отметить, что точность результатов зависит от количества сделанных попыток и запомненных распознаваемых образов.
Библиографический список
- Хайкин С. Нейронные сети. М.: Издательский дом “Вильямс”, 2006.
- Бодянский Е.В. Искусственные нейронные сети: архитектура, обучение и применение. Харьков: Телтех, 2004.