Введение
В настоящее время статистические методы широко применяются в сфере информационных технологий для анализа данных. Целью исследования является оценка производительности системы при внедрении новых алгоритмов в систему [1]. Предположим, разработано три алгоритма A1, A2 и А3 для существующей системы обработки информации.
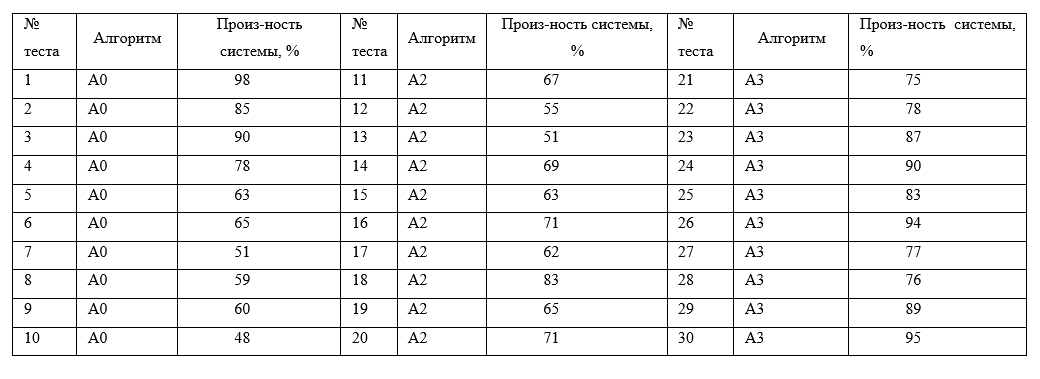
Чтобы оценить, как изменится производительность системы при внедрении алгоритмов, проведено их тестирование на различных наборах данных. Результаты тестов алгоритмов и производительность системы представлены в таблице 1.
Таблица 1. Производительность системы для трех алгоритмов
Выдвинута нулевая гипотеза – производительность системы принадлежит одному и тому же распределению. То есть, влияние фактора (внедрение нового алгоритма) несущественно. Выдвинута альтернативная гипотеза влияние фактора (внедрение нового алгоритма) существенное. Необходимо выяснить, влияет ли тип алгоритма на производительность системы.
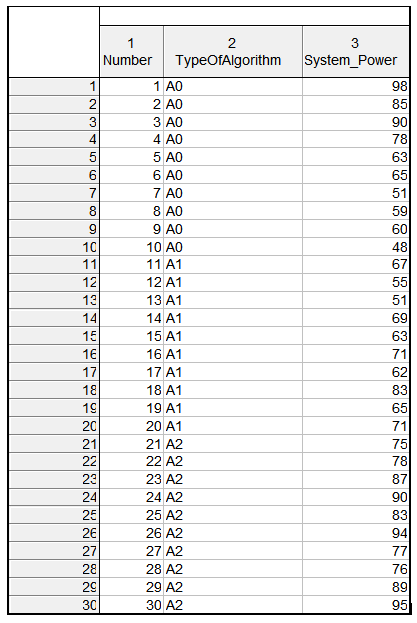
В пакете Statistica были созданы три переменные Number, TypeOfAlgorithm и System_Power.
В качестве зависимой переменной была выбрана производительность системы, а независимой – тип алгоритма. Для группировки были выбраны все переменные.
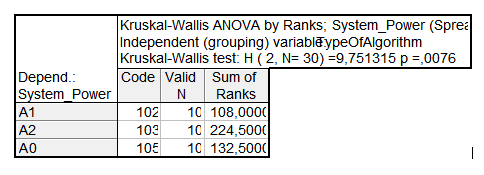
Результат теста Краскела – Уоллиса представлен на рисунке 1.
Рисунок 1. Результат теста Краскела – Уоллиса
В приведенных результатах приняты следующие обозначения: Codes – уникальный код группы (число); Valid N – число значений в группе; Sum of Ranks – сумма рангов; H – статистика Краскела – Уоллиса; р – вероятность принятия гипотезы Н0.
Анализируя суммы рангов, представленные на рисунке 1, можно говорить о влиянии уровня фактора (тип алгоритма) на производительность. Из результатов видно, что лучшая производительность системы обеспечивается за счет алгоритма A2, а худшая – за счет А1. В статистике Краскела – Уоллиса вычисляется сумма квадратов разностей средних рангов в группе и среднего ранга по всей выборке. Если верна гипотеза и влияние фактора незначимо, то значение статистики мало. Из рисунка 1 видно, что p=0.0076. Поскольку заданный уровень значимости α = 0.05 больше p=0.0076, то нулевая гипотеза отвергается в пользу альтернативной гипотезы H1 – влияние фактора (тип алгоритма) на производительность системы существенное.
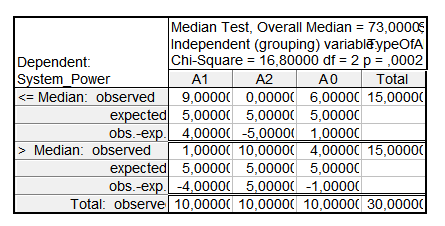
На следующем этапе был сделан медианный тест [2]. Результаты медианного теста представлены на рисунке 2. В верхней части таблицы приведены количества рангов в группах, которые были меньше или равны медиане. В нижней части таблицы – аналогичные значения, превышающие значение медианы.
Рисунок 2. Результат медианного теста
Были проанализированы результаты на качественном уровне. По значению разности предсказанных и полученных значений (obs.-exp.) можно сделать следующие выводы:
- верхняя половина таблицы – максимальное значение указывает на худший тип алгоритма (в данном случае А1);
- нижняя половина таблицы – максимальное значение указывает на лучший алгоритм (в данном случае А2).
Количественная оценка статистики свидетельствует о том, что нулевую гипотезу можно принять с вероятностью p = 0.0002, что намного меньше уровня значимости, следовательно, принимается гипотеза H1 – влияние фактора (тип алгоритма) на производительность системы существенное.
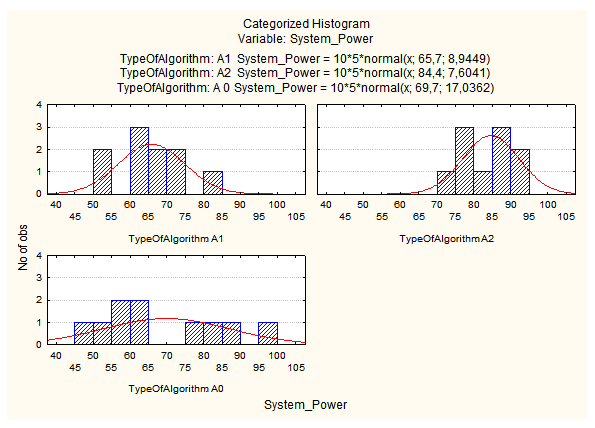
В системе Statistica при проведении рангового однофакторного анализа были построены гистограммы распределения производительности системы.
На построенных гистограммах сплошной линией проведены гауссовы распределения с соответствующими параметрами. Визуальный анализ подтверждает (рис. 3), что лучший алгоритм A2, т.к. при этом алгоритме минимальная и максимальная производительности системы больше, чем при алгоритмах A0 и A1, Этот алгоритм обеспечивает 85% значений производительности системы в интервале [75, 95], что значительно лучше, чем в других группах [2].
Рисунок 3. Гистограммы распределения производительности системы
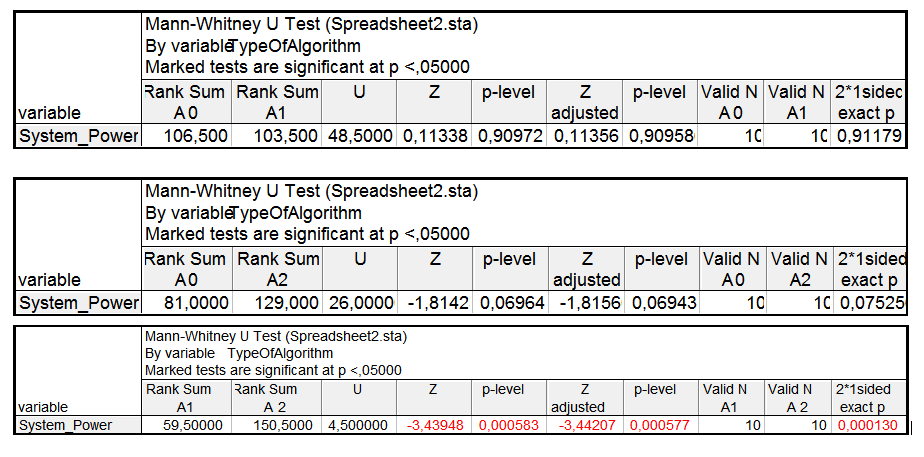
Для проверки критерия Манна – Уитни сформулирована нулевая гипотеза исходные две выборки – однородны, соответственно гипотеза H1утверждает, что выборки не однородны, т. е. влияние фактора значимо. Результаты теста Манна – Уитни для всех возможных пар выборок представлены на рис. 4.
Рисунок 4. Результаты теста Манна – Уитни для A1-A0, A0-A2, А1-А2
В приведенных таблицах приняты следующие обозначения: Rank Sum Ti – сумма рангов выборки Тi; U –статистика Манна – Уитни для малых выборок; p – level – вероятность принятия гипотезы Н0; p – level – скорректированная вероятность принятия гипотезы Н0; 2*1 sided exact p – здесь вероятность p равна 1 минус кумулятивная односторонняя вероятность соответствующей статистики Манна – Уитни, Valid N – объем выборки; Rank Sum Tj – сумма рангов выборки Тj.
Анализ результатов:
- Для двух алгоритмов (уровней факторов) А0-А1 статистика U достаточно велика и нулевую гипотезу можно принять с вероятностью
р = 0,9. При 5% уровне значимости гипотезу Н0 следует признать верной, то есть влияния фактора незначительное и две выборки однородны. - Сравнивая алгоритмы А0 и А2, видно, что две выборки можно признать однородными, так как p больше уровня значимости.
- Что касается алгоритмов А1 и А2, то нулевую гипотезу можно принять с вероятностью р = 0,000583, что меньше уровня значимости. На основании этого нулевую гипотезу отвергаем в пользу альтернативной – влияния фактора значительное и выборки неоднородны.
Так как предварительный ранговый однофакторный анализ подтвердил гипотезу о значимом влиянии фактора, было оценено это влияние количественно в рамках дисперсионного анализа.
Проверим нулевую гипотезу – влияние фактора на распределение данных не существенно.
На рисунке 5 представлены результаты дисперсионного анализа.
Рисунок 5. Гистограммы распределения производительности системы
Статистика Фишера F= 6,79 незначимо отличается от единицы с вероятностью p=0.004, что значительно меньше уровня значимости. Следовательно, нулевую гипотезу следует отвергнуть в пользу альтернативной гипотезы H1 – влияние фактора существенно.
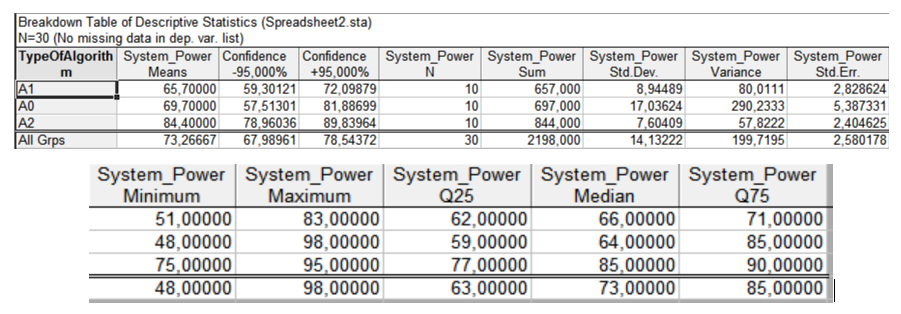
На рисунке 6 представлено влияние алгоритма на производительность системы.
Рисунок 6. Влияние алгоритма на производительность системы
Полученные результаты (средние значения) свидетельствуют о существенном различии точечных характеристик для различных групп.
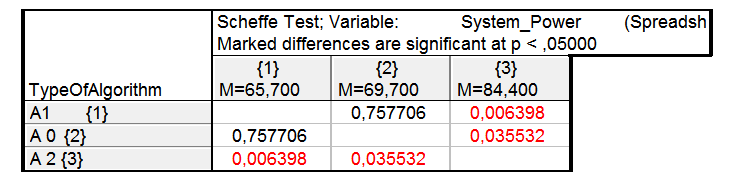
Результат сравнения средних по методу Шеффе для различных пар уровней приведен на рис. 7.
Рисунок 7. Результаты теста Шеффа
В результата проверки гипотезы о незначимом различии средних, для пары А1 – А2 вероятность нулевой гипотезы равная 0.00639 много меньше уровня значимости. Поэтому нулевая гипотеза отклоняется, влияние фактора значительное. Для пары А2 – А0 вероятность нулевой гипотезы равная 0.0035532 много меньше уровня значимости. Поэтому нулевая гипотеза отклоняется, влияние фактора значительное. Для пары А0 – А1 вероятность нулевой гипотезы равная 0.75 много больше уровня значимости. Поэтому нулевая гипотеза принимается, то есть влияние фактора незначительное.
В результате проверки критерия Краскела-Уоллиса были проанализированы суммы рангов. Было выявлено влияние уровня фактора (тип алгоритма) на производительность системы. Анализ показал, что лучшая производительность системы обеспечивается за счет алгоритма A2, а худшая – за счет А1. Медианный тест показал, что худший тип алгоритма в данном случае А1, а лучший – А2. Визуальный анализ при помощи гистограмм распределения производительности подтвердил, что лучший алгоритм A2, т.к. при этом алгоритме минимальная и максимальная производительности системы больше, чем при алгоритмах A0 и A1, Этот алгоритм обеспечивает 85% значений производительности системы в интервале [75, 95], что значительно лучше, чем в других группах. С помощью критерия Манна – Уитни была проверена нулевая гипотеза о том, что исходные две выборки – однородны, а значит влияние фактора незначимо. Проверка выявила, что для алгоритмов А1 и А2 нулевую гипотезу можно принять с вероятностью р = 0,000583, что меньше уровня значимости. На основании этого нулевая гипотеза была отвержена в пользу альтернативной гипотезы – влияния фактора значимо, и выборки неоднородны. Так как предварительный ранговый однофакторный анализ подтвердил гипотезу о значимом влиянии фактора, было оценено это влияние количественно в рамках дисперсионного анализа. Проверка показала, что статистика Фишера F= 6,79 незначимо отличается от единицы с вероятностью p=0.004, что значительно меньше уровня значимости. Следовательно, нулевая гипотеза была отвержена в пользу альтернативной гипотезы H1 – влияние фактора существенно. Для сравнения средних значений был использован тест Шеффа. Этот тест показал, что для пары А1 – А2 вероятность нулевой гипотезы равная 0.00639 много меньше уровня значимости. Поэтому нулевая гипотеза отклоняется, влияние фактора значительное. Для пары А2 – А0 вероятность нулевой гипотезы равная 0.0035532 много меньше уровня значимости. Поэтому нулевая гипотеза отклоняется, влияние фактора значительное. Для пары А0 – А1 вероятность нулевой гипотезы равная 0.75 много больше уровня значимости. Поэтому нулевая гипотеза принимается, то есть влияние фактора незначительное [3].
Библиографический список
- Шеффе Г. Дисперсионный анализ. – М., 1963. -22-29 с.
- Боровиков В.П. Популярное введение в современенный анализ данных в системе STATISTICA. – М.:Горячая линия – Телеком, 2013. – 288 с.
- Симчера В.М. Методы многомерного анализа статистических данных. М.: Финансы и статистика, 2008. -400 с.