Каждая конкретная механическая система может обладать или не обладать свойством устойчивости движения. Обеспечение условий устойчивого движения принадлежит к числу основных задач при проектировании.
Существуют два вида устойчивого движения механических систем. В первом из них начальные возмущения с течением времени асимптотически стремятся к нулю, во втором, оставаясь малыми, полностью не исчезают.
Асимптотическая устойчивость невозмущённого движения системы обеспечивается при выполнении необходимого и достаточного условий. В качестве таких условий предлагается, чтобы все корни характеристического уравнения, определяемые решением системы дифференциальных уравнений (1) имели отрицательные вещественные части /1/.
Общий вид системы дифференциальных уравнений движения НПМ представлен в следующем виде:
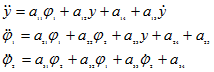 (1)
(1)![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
где,
![]() момент инерции несущей рамы манипулятора, относительно ребра опрокидывания, кг с2 м.;
момент инерции несущей рамы манипулятора, относительно ребра опрокидывания, кг с2 м.;
![]() момент инерции остова трактора относительно ребра опрокидывания, кг с2 м ;
момент инерции остова трактора относительно ребра опрокидывания, кг с2 м ;
m – приведённая масса груза, кг;
m1- масса несущей рамы, кг;
m2- масса трактора, кг;
![]() -расстояние между опорами несущей рамы, м;
-расстояние между опорами несущей рамы, м; ![]() колея задних колёс трактора, м;
колея задних колёс трактора, м;
L- вылет стрелы, м;
С- приведённая жёсткость грузового подвеса, Н/м;
С1-жёсткость опорных элементов несущей рамы манипулятора, Н/м;
С2, С5-жёсткость опорных элементов трактора, Н/м;
С3-жёсткость трехточечной навесной системы трактора, Н/м;
к, к1, к2, к5-коэффициенты вязкого трения опорных элементов и гидроцилиндра манипулятора, кг с/м.
Для получения характеристического уравнения необходимо, чтобы система уравнений (1) была однородной. Тогда принимая во внимание то, что возмущение является кратковременным (постоянные внешние воздействия нами учтены при составлении уравнения), а устойчивость движения навесного погрузочного манипулятора рассматривается после снятия возмущающего воздействия; получим для правых частей системы уравнений ![]() Действием моментов трения можно пренебречь
Действием моментов трения можно пренебречь ![]()
Составим характеристическое уравнение для системы (1). После несложных преобразований получим характеристическое уравнение в виде многочлена шестой степени:
где m0=1
m1=a33-a31;
m2=a31 a33-a31-2a21;
m3=a31(a31-a21)+a21(a33+a32);
m4=2a21 a31-a31 a21 a33- a32 a22+a21-a11 a13;
m5=a13 (a32-a22 -a21 a31)-a33 (a11a33-a221);
m6=a21(a22a32-a21a31)+a11a31a33;
Все коэффициенты mi характеристического уравнения в общем случае не имеют нулевых значений. Таким образом, характеристическое уравнение рассматриваемой системы в общем случае не имеет нулевых корней. Выполнение этих условий влечёт за собой асимптотическую устойчивость движения системы.
Конкретные условия устойчивости движения агрегата заключается в том,что коэффициенты характеристического уравнения (2), а также определить, составленные из этих коэффициентов имеют положительные знаки/2/
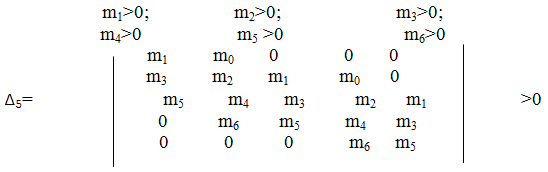
Подставив в выражения mi значения коэффициентов aiј, найдём условия устойчивости движения НПМ в виде явных зависимостей между основными его параметрами.
Обозначив
и учитывая, что I1, I2, и m всегда >0, получим:
.gif)
![]() (3)
(3)
Если значения mi подставить в последнее из условий устойчивости Д5>0, получим ещё одно соотношение между параметрами манипулятора, обеспечивающее устойчивое его движение вокруг ребра опрокидывания. Однако эта зависимость получается очень сложной.
Некоторые из условий (3) не накладывают ограничений на параметры системы. Например, очевидно, что всегда m1>0, m2>0, m3>0, остальные неравенства могут и не выполнятся.
Анализируя подробнее полученные условия, следует обратить внимание на параметр c3, который, судя по знакам выражений, в которые он входит, является стабилизирующим фактором, в том случае, если I2>I1,а это значит, что целесообразно его увеличение.
Заменим в расчётной схеме упругое звено с3, абсолютно жёстким. Получим новую расчётную схему (рис.1), выполненную по авт.св .№ 1126533.
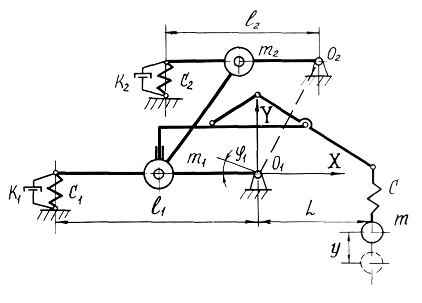
а)
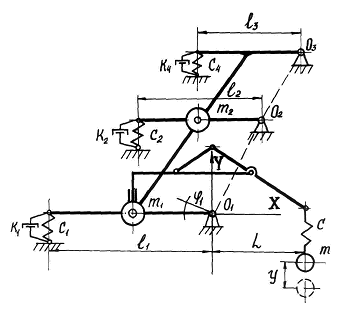
б)
Рисунок 1 – Схема навесного погрузочного манипулятора:
а) экспериментальная по а.с. №1126533;
б) с блокировкой переднего моста.
Выбрав в качестве обобщённых координат линейное перемещение груза у и угловое перемещение несущей рамы манипулятора ц1, составим уравнения движения новой системы, учитывая при этом, что;
![]()
.gif) (4)
(4)
где ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Таким образом, в данном случае движение описывается системой двух неоднородных линейных дифференциальных уравнений второго порядка.
Очевидно, что действие параметров с1 и с2 аналогично, однако их увеличение сопряжено с рядом технических трудностей и поэтому вряд ли оправдано. Достичь их увеличения можно косвенным путём, а именно обеспечить блокировку переднего моста трактора, что позволит использовать жёсткость его опорных элементов. Тогда расчётная схема может быть представлена в виде, показанном на рис. 1, а её движение описано следующей системой уравнений:
.gif) (5)
(5)
где
Зависимость (5) выражает устойчивость невозмущённого движения вообще (устойчив, неустойчив), т.е. поведение системы после снятия возмущающего воздействия и не даёт количественной оценки отклонения от начального положения при возмущении. Хотя движение может быть асимптотически устойчивым, а амплитуда этого движения может превышать установленные пределы.
Критическим в отношении потери устойчивости навесного погрузочного манипулятора считаем случай нарушения контакта, хотя бы одной из опор с основанием под действием динамических сил. Как указано /3/ отрыв опоры от основания в некоторых случаях близок к опрокидыванию. Кроме того, отрыв опоры от основания и последующие её нагружения вызывают значительные динамические ударные нагрузки /4/, а непостоянный характер связей опорных элементов с основанием вызывает значительную сложность в исследовании устойчивости.
В связи с этим некоторые исследователи вводят понятие “практической ” устойчивости /5/. Трудности анализа “практической” устойчивости состоит в том, что для систем подобных рассматриваемой не существует достаточно простых и достаточно общих критериев. По существу единственный способ проверки устойчивости заключается в построении реакции обобщённой координаты на возмущающее воздействие.
Для определения реакции обобщённой координаты на возмущающее воздействие, как правило проводится численное решение систем уравнения.
В качестве критерия принимаем /3/:
где ![]() реакция i-ой опоры.
реакция i-ой опоры.
Библиографический список
- Кузьмин П.А. Малые колебания и устойчивость движения. Наука, 1973, 206 с.
- Дубинин В.Ф. Исследование работы грейферных погрузчиков на животноводческих фермах. Автореф. дис. на соиск. учен. степени канд.техн.наук. – Саратов, 1971.
- Комаров М.С. Динамика грузоподъемных машин, изд. 2-е – М.-К.: Машгиз, 1962, с. 267.
- Мельников С.В., Алешкин В.Д., Рощин П.М. Планирование эксперимента в исследованиях сельскохозяйственных процессов. – Д.: Колос, 1960. – 166 с.
- Голомидов А.М. Эксплуатационные свойства автомобилей с приводом на передние колеса. – М.: Машиностроение,1986. – 112 с.


