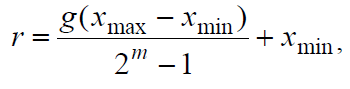На сегодняшний день задачи оптимизации возникают в различных областях знаний. В частности, в математического анализе, существует важная задача нахождения максимума функции.
Решения такой задачи методами математического анализа не всегда могут дать точные результаты [1]. В данной статье предлагается использовать генетический алгоритм для решения одной из задач оптимизации. Эффективным инструментом для разработки генетического алгоритма является C#.
Постановка задачи следующая: найти максимум любой функции от двух переменных, на заданном интервале, используя целочисленное (бинарное) кодирование. Например, найти максимум функции f (x,y) = sin (2*PI*x) + cos (2*PI*y) + 18 на интервале [-2, 2] по x и y.
Поставленная задача была решена посредством метода генетического алгоритма.
Генетический алгоритм включает в себя следующие шаги:
1. формирование начальной популяции.
2. оценивание популяции.
3. селекция.
4. скрещивание.
5. мутация [2].
На рисунке 1 приведена структурная схема генетического алгоритма.
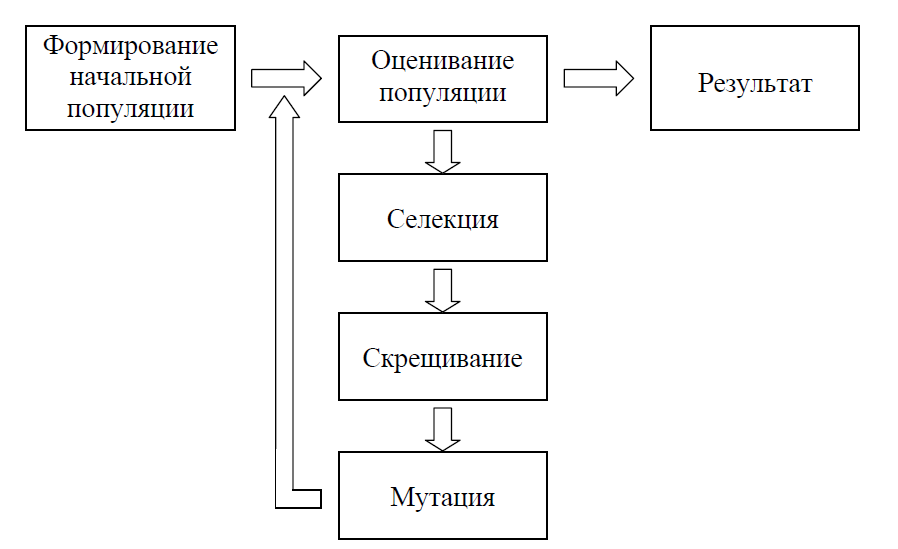Рисунок 1. Схема генетического алгоритма
В качестве кодирования генотипов X и Y было выбрано целочисленное или бинарное кодирование. В качестве метода селекции был выбран рулеточный отбор наиболее приспособленных особей в популяции. В качестве метода скрещивания выбранных особей был использован одноточечный кроссинговер. Мутация особей была реализована посредством инверсии битов хромосом по всей длине, то есть многоточечный подход. Длительность эволюции в программе была определена посредством ограниченности числа поколений.
В качестве целевой функции может быть использована любая функция от двух переменных. Таким образом, в программе было задано два генотипа X и Y, то есть два параметра. Каждая хромосома представляет собой битовую строку, разрядность которой = 10. Для преобразования каждого генотипа к его фенотипу была использована формула:
Оценка особи происходит на основании вычисления приспособленности каждой особи на основании целевой функции. Если f(Gi) > f(Gj), то i-я особь считается более приспособленной, чем j-я особь [3].
Основные параметры, которые задаются для генетического алгоритма:
1) количество поколений;
2) численность популяции;
3) вероятность скрещивания;
4) тип скрещивания – одноточечный кроссинговер;
5) вероятность мутации;
6) тип оператора мутации – побитовая инверсия хромосомы (битовая мутация).
Каждая особь в популяции описывается с помощью класса Individual. Каждая особь имеет два генотипа по X и Y, фенотипа для X и Y, который вычисляется по формуле перехода, значения функции приспособленности для особи, вероятность попадания в родительский массив, границы попадания в родительский массив (левая и правая).
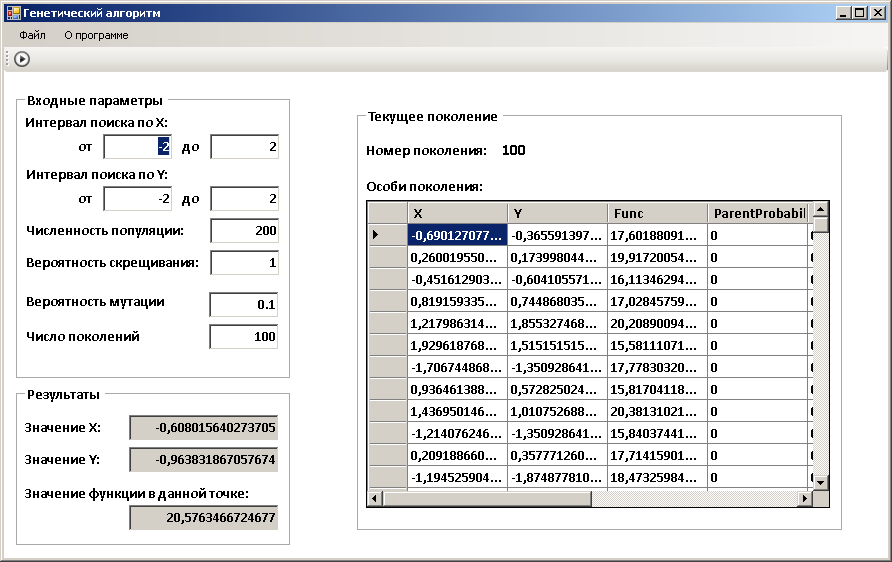
В качестве примера была использована функция от двух переменных f (x,y) = sin (2*PI*x) + cos (2*PI*y) + 18 на интервале [-2, 2] по x и y.
На рисунке 1 приведены результаты работы генетического алгоритма, а также заданные параметры.
Рисунок 1. Результаты работы генетического оператора
Если использовать классические метода математического анализа, то при вычислении максимума функции значение будет равно 20. Однако, используя генетический алгоритм может получить более точное значение. В данном случае при 100 поколениях получено значение = 20.57. Разница 0.57 может показаться незначительной. Но при решении задач оптимизации эта разница играет важную роль.
Библиографический список
- Данута Рутковская, Мачей Пилиньский, Лешек Рутковский. Нейронные сети, генетические алгоритмы и нечеткие системы. Горячая Линия – Телеком, 2007.
- Гладков Л. А., Курейчик В. В., Курейчик В. М. Генетические алгоритмы: Учебное пособие. 2-е изд. М: Физматлит, 2006.
- Скобцов Ю. А. Основы эволюционных вычислений. Донецк: ДонНТУ, 2008.