1.    Общие положения о применении критерия  при проверке статистических гипотез

Критерий основан на сравнении эмпирической гистограммы распределения случайной величины с её теоретической плотностью. Диапазон изменения экспериментальных данных разбивается на k  интервалов, и рассчитывается значение статистики по формуле:

                                                                                                                       (1)

где  – количество значений случайной величины, попавших в i-й интервал;  – объём выборки;  F(x)– гипотетический теоретический закон распределения вероятностей случайной величины;  – теоретическая вероятность попадания случайной величины в i-й интервал.[1, с. 204]

Принято считать, что статистика критерия имеет распределение, близкое к распределению . Правило проверки гипотезы следующее: если

                                                                                                                 (2)

то на уровне значимости , т.е. с достоверностью , гипотеза о распределении отклоняется (Рисунок 1).  – критическое значение критерия для уровня значимости  и при числе степеней свободы f.[1, c. 205]

Рисунок 1. График распределения  с областью отклонения гипотезы [2, c. 169]

Если параметры гипотетического распределения определяются непосредственно по самой выборке, то число степеней свободы  определяется по формуле:

f = k – m – 1,                                                                                                                             (3)

где k - число интервалов группирования, m - количество параметров, оцениваемых по выборке [3, c. 8].

2.    Применение критерия  при проверке гипотезы о согласии распределения с нормальным

         Для расчёта значения критерия при проверке статистической гипотезы о соответствии закона распределения случайной величины выборки нормальному необходимо найти теоретические значения частот попадания случайной величины в каждый интервал гистограммы плотности нормального распределения с учётом объёма выборки, выборочного среднего и выборочного среднего квадратичного отклонения.

Исходя из этих положений, формула (3) принимает следующий вид:

f = k – 3,                                                                                                                              (3)

При этом k в случае унимодального нормального распределения в соответствии с рекомендациями из [3, с. 14] принимает такие значения, при которых не более чем в двух крайних интервалах частоты меньше либо равны 1.

Для нахождения гипотетической гистограммы нормального распределения можно использовать следующий алгоритм:

1. Рассчитать значения выборочного среднего 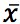 и выборочного среднего квадратичного отклонения s.
2. Для каждого интервала определить середину 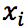 и частоту попадания случайной величины .
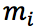3. Вычислить отношение разности 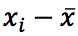 к выборочному среднему квадратичному отклонению: .
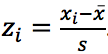4. По найденным на предыдущем шаге значениям рассчитать значение соответствующей плотности стандартного нормального распределения: .
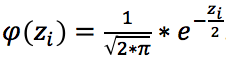5. Для каждого интервала найти значение .
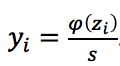6. Вычислить теоретические значения вероятности попадания случайной величины в соответствующие интервалы по формуле 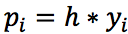, где h - ширина интервала.
7. Определить гипотетическое значение частот попадания в соответствующие интервалы как произведение .
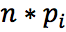8. Для каждого интервала определить значение расхождения .
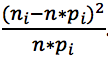9. Наконец, вычислить значение статистического критерия 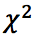 по формуле (1).

Имея значение статистического критерия, можно найти достигнутый уровень значимости , что позволит оперировать ещё одним правилом проверки статистической гипотезы: достигнутый уровень значимости  должен превысить выбранное критическое значение уровня значимости . Критический уровень значимости  представляет собой вероятность того, что вычисленное значение критерия  превысит критическое значение . На практике значение  выбирают от 0.05 до 0.001 в зависимости от объёма выборки, однако конкретных практических рекомендаций о способе выбора данного значения нет.

Достигнутый уровень значимости можно определить с помощью встроенной функции Microsoft Excel: CHISQ.DIST.RT(X, Deg_freedom), где X – значение, для которого определяется уровень значимости; Deg_freedom – число степеней свободы, которое определяется по формуле (4). [4]

Таким образом, применяя данный алгоритм, можно реализовать проверку согласия распределения эмпирической выборки с нормальным.

1. Кобзарь А. И. Прикладная математическая статистика. Для инженеров и научных работников. – М.: ФИЗМАТЛИТ, 2006 – 816 с. – ISBN-5-9211-0707-0.
2. Осипов А.Л., Храпов В.Н. Эконометрика: Учебно-методический комплекс для дистанционного обучения. – Новосибирск: СибАГС, 2002. – 173 с.
3. ГОСТ Р 50.1.033-2001 Прикладная статистика. Правила проверки согласия опытного распределения с теоретическим. Часть 1. Критерии типа хи-квадрат. – Москва: Госстандарт России – 91 с.
4. Excel Help [Электронный ресурс] – URL: https://support.office.com/en-us/article/CHISQ-DIST-RT-function-dc4832e8-ed2b-49ae-8d7c-b28d5804c0f2 (дата обращения: 12.05.2016)

Все статьи автора «Фатихов Наиль Жаугарович»