УДК 531.8; 621.8 (28.001.2); 621.73
АНАЛИТИЧЕСКИЙ РАСЧЕТ КИНЕМАТИЧЕСКИХ ХАРАКТЕРИСТИК МЕХАНИЗМА ПРИЖИМА ВЫТЯЖНОГО ПРЕССА ДВОЙНОГО ДЕЙСТВИЯ
Явтушенко Александр Викторович
Запорожский национальный технический университет, Украина
кандидат технических наук,
доцент кафедры обработки металлов давлением
АннотацияРассмотрены вопросы аналитического расчета кинематических характеристик рычажного восьмизвенного механизма прижима механического пресса двойного действия для глубокой вытяжки, обеспечивающего длительный выстой ползуна в нижнем положении на заданном угле поворота главного вала. Представлены аналитические зависимости для определения углов положения ведущего кривошипа в характеристических точках траектории функции положения, величины отклонения ползуна от нижнего положения. Представленные зависимости дают возможность проектирования механизма по заданному углу выстоя и углу стояния ползуна после окончания процесса вытяжки.Ключевые слова: длительность выстоя, механизм, пресс, угол выстоя, угол стояния, функция положения, экстремум
ANALYTICAL CALCULATION OF KINEMATIC CHARACTERISTICS OF CLAMPING MECHANISM MECHANICAL PRESSES DOUBLE ACTION
Javtoushenko Aleksandr Viktorovich
Zaporizhzhya National Technical University, Ukraine
Ph.D., Assistant Professor of metal forming
AbstractConsidered are the issues of analytical calculation of kinematic characteristics lever Posmitnogo of clamping mechanism mechanical presses double action for deep drawing for the long dwell slider in the lower position at a given angle of rotation of the main shaft. Analytical dependences for determination of the angles of the leading crank in the characteristic points of the trajectory functions Polo-ment, the deflection of the slide from the lower position. Presented according to enable the design of the mechanism at the specified corner of the stand and angle of elevation of the slide after the end of the process of extrusion.Keywords: angle of elevation, duration of you are standing, function of position, mechanism, to the extreme corner of a stand
Библиографическая ссылка на статью:
Явтушенко А.В. Аналитический расчет кинематических характеристик механизма прижима вытяжного пресса двойного действия // Современная техника и технологии. 2014. № 7 [Электронный ресурс]. URL: https://technology.snauka.ru/2014/07/4164 (дата обращения: 04.06.2025).
Для выполнения технологической операции глубокой вытяжки листового материала используются специализированные вытяжные прессы двойного действия, имеющие дополнительный механизм для прижима заготовки. Основное функциональное назначение механизма состоит в обеспечении прижима заготовки с постоянным усилием при заданном угле поворота главного вала.
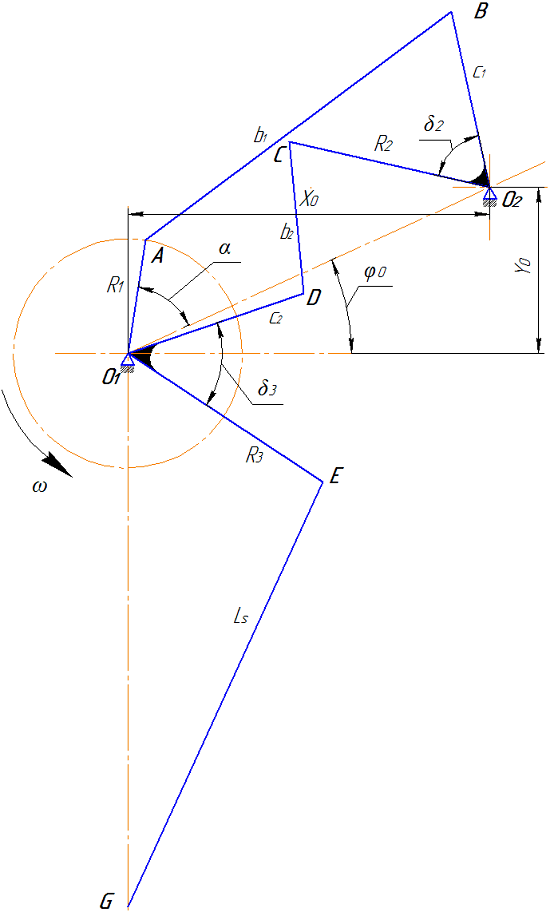 Рис. 1 – Схема механизма прижимного ползуна
Рис. 1 – Схема механизма прижимного ползунаВ современных вытяжных прессах наибольшее распространение находит восьмизвенный рычажный механизм прижима, состоящий из последовательно соединенных трех простейших механизмов (рис. 1). Известно, что рычажный механизм не может обеспечить абсолютный длительный выстой ползуна при значительном угле поворота ведущего вала [1], поэтому практически на участке рабочего хода обеспечивается движение ползуна с предельным отклонением от нижнего положения не превышающим заданное значение, т. е. всегда выполняется условие
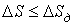 . (1)
. (1)Структурный синтез составного механизма показывает, что в общем случае может быть обеспечено не менее восьми экстремальных положений ведомого звена, т. е. восемь экстремумов функции положения в промежутке угла поворота ведущего звена  . На рис. 2 показан типовой график движения прижимного Sп и вытяжного Sв ползунов пресса. На рисунке обозначено: αквп, αкнп – соответственно, угол крайнего верхнего и крайнего нижнего положения вытяжного ползуна; αнп, αкп – соответственно угол начала и конца прижима, т. е. выстоя прижимного ползуна; αс – угол выстоя прижимного ползуна после вытяжки; Sp – рабочий ход вытяжного ползуна.
. На рис. 2 показан типовой график движения прижимного Sп и вытяжного Sв ползунов пресса. На рисунке обозначено: αквп, αкнп – соответственно, угол крайнего верхнего и крайнего нижнего положения вытяжного ползуна; αнп, αкп – соответственно угол начала и конца прижима, т. е. выстоя прижимного ползуна; αс – угол выстоя прижимного ползуна после вытяжки; Sp – рабочий ход вытяжного ползуна.
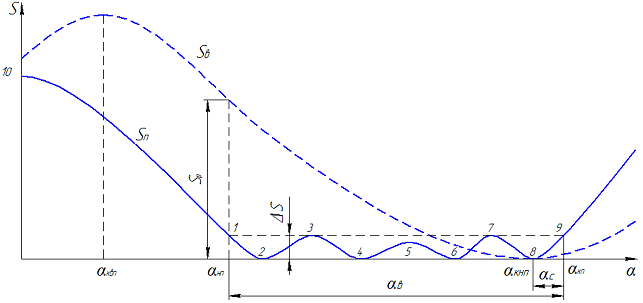 Рис. 2 – Графики движения ползунов вытяжного пресса
Рис. 2 – Графики движения ползунов вытяжного прессаЕсли максимальное отклонение на участке рабочего хода удовлетворяет условию (1), то всегда существует еще две характерные точки на графике функции положения механизма, в которых также выполняется это условие. На рис. 2 эти точки обозначены соответственно 1 и 9. Таким образом, в общем случае участок «псевдовыстоя» ползуна определяется координатами крайних точек α1 и α9. Интервал угла поворота ведущего кривошипа 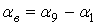 и есть интервал поворота, на котором обеспечивается выполнение условия (1).
При проектировании механизма прижимного ползуна уже на этапе эскизного проектирования возникает необходимость определения геометрических характеристик, обеспечивающих удовлетворение технологических требований. Требуется определить значения отклонений ΔSi (i = 1, …, 10) на участке рабочего хода, значения угла αв выстоя ползуна, значения угла α1, определяющего возможное начало процесса вытяжки и угла α9, определяющего начало отхода прижимного ползуна после совершения вытяжки. Отклонения и значения соответствующего угла αi для каждой экстремальной точки могут быть определены при известной функции положения механизма [2] путем поиска локального минимума. Однако такой метод обеспечивает решение задачи в численном виде только для определенной комбинации исходных данных.
Частично аналитическое определение характеристик механизма рассмотрено в работе [1], однако для практического использования результатов необходим более широкий анализ кинематики механизма.
Целью настоящей статьи является разработка алгоритма аналитического определение экстремальных отклонений ползуна и значений соответствующих углов αi для каждой экстремальной точки.
Существование 10 точек экстремума функции положения ведомого звена обеспечивается тем, что в этих точках звенья механизма занимают определенные положения. Положение механизма, при котором одно из звеньев становится в крайнее положение, будем называть предельным положением механизма. На рис. 3 показаны пять положений первых двух механизмов. Первое предельное положение, показанное штрихпунктирной линией, и обозначенное индексами ”10”, соответствует крайнему правому положению первого механизма, когда звенья O1A и AB располагаются на одной линии, а ползун находится в крайнем верхнем положении.
и есть интервал поворота, на котором обеспечивается выполнение условия (1).
При проектировании механизма прижимного ползуна уже на этапе эскизного проектирования возникает необходимость определения геометрических характеристик, обеспечивающих удовлетворение технологических требований. Требуется определить значения отклонений ΔSi (i = 1, …, 10) на участке рабочего хода, значения угла αв выстоя ползуна, значения угла α1, определяющего возможное начало процесса вытяжки и угла α9, определяющего начало отхода прижимного ползуна после совершения вытяжки. Отклонения и значения соответствующего угла αi для каждой экстремальной точки могут быть определены при известной функции положения механизма [2] путем поиска локального минимума. Однако такой метод обеспечивает решение задачи в численном виде только для определенной комбинации исходных данных.
Частично аналитическое определение характеристик механизма рассмотрено в работе [1], однако для практического использования результатов необходим более широкий анализ кинематики механизма.
Целью настоящей статьи является разработка алгоритма аналитического определение экстремальных отклонений ползуна и значений соответствующих углов αi для каждой экстремальной точки.
Существование 10 точек экстремума функции положения ведомого звена обеспечивается тем, что в этих точках звенья механизма занимают определенные положения. Положение механизма, при котором одно из звеньев становится в крайнее положение, будем называть предельным положением механизма. На рис. 3 показаны пять положений первых двух механизмов. Первое предельное положение, показанное штрихпунктирной линией, и обозначенное индексами ”10”, соответствует крайнему правому положению первого механизма, когда звенья O1A и AB располагаются на одной линии, а ползун находится в крайнем верхнем положении.
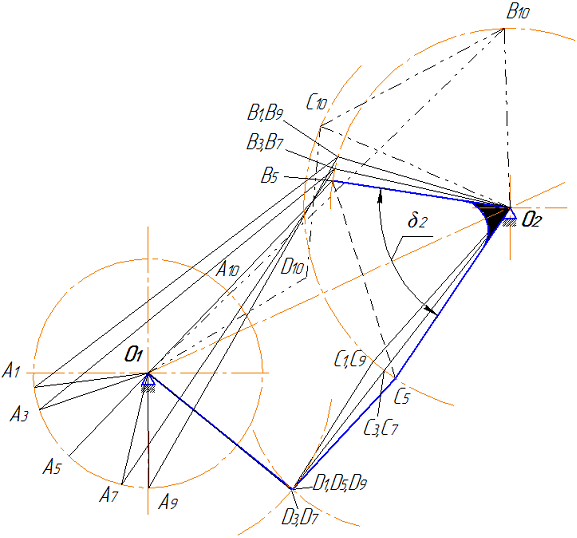 Рис. 3 – Экстремальные положения первых двух механизмов
Рис. 3 – Экстремальные положения первых двух механизмовПротивоположное положение, когда указанные звенья находятся на одной линии, но направлены в разные стороны, соответствует крайнему левому положению механизма. На рисунке это положение обозначено индексами ”5”. Механизм будет обеспечивать выстой ползуна, если в этом предельном положении точка С второго механизма переходит линию, соединяющую шарниры O2 и D. При таком условии точка С проходит предельное положение, когда на одной линии располагаются звенья O2С и СD второго механизма. Эти положения обозначены индексами ”3” и ”7”. Кроме этого имеется еще два предельных положения обозначенные индексами ”1” и ”9”, симметричных положению ”5”, когда точка Dнаходится в том же положении, что и при положении ”3”. Таким образом, при повороте ведущего кривошипа O1A на угол α19 из положения A1 в положение A9 точка С последовательно проходит положения С1, С3, С5, С7 и С9, а рычаг O2Ссовершает качательное движение на относительно малом угле размаха. При оптимальном выборе размеров рычага СD и коромысла O1D ведомый рычаг O1F второго четырехзвенника будет совершать качание не весьма малом угле размахаΔφ (рис. 4). Из рисунка следует, что если линия движения ползуна является биссектрисой угла Δφ, то точка F при движении от одного крайнего положения к другому четыре раза проходит через среднее положение (положения F2, F4, F6,F8), соответствующее абсолютному нижнему положению ползуна. Таким образом, обеспечиваются все положения, обозначенные на рис .1.
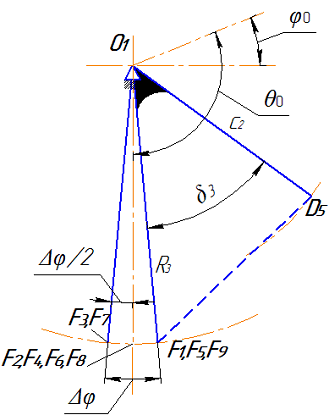 Рис. 4 – Угол качания звена O1F
Рис. 4 – Угол качания звена O1FИз рисунка следует, что точка F, а соответственно и прижимной ползун совершают относительно малые вертикальные перемещения.
Для определения указанных геометрических характеристик механизма необходимо последовательно рассмотреть несколько его предельных положений.
Угол α5, определяющий положение ”5” механизма определяется по известной формуле [1, 2]
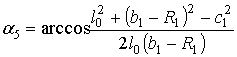 . (2)
. (2)На рис. 5 показано положение сдвоенного четырехзвенника в положениях ”3”, ”5” и ”7”. Угол размаха Δφ рычага O1F или рычага O1D есть угол между линиями O1D3 и O1D5. Из треугольника O1B5O2 по теореме косинусов находим
 . (3)
. (3)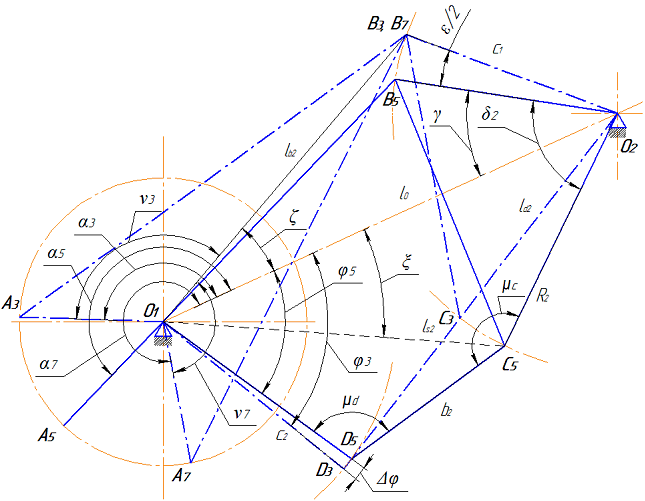 Рис. 5 – Определение угла размаха рычага O1D
Рис. 5 – Определение угла размаха рычага O1DВсе размеры звеньев механизма указаны на рис. 1. Размер l0 есть расстояние между центрами O1 и O2. Из треугольника O1O2С5 находим расстояние ls2 = O2С3
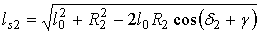 .
.Из этого же треугольника определяется угол ξ
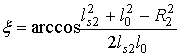 .
.Из треугольника O1C5D5 находится угол φ5
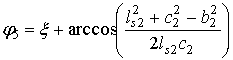 .
.Угол φ3 находится из анализа положения ”3”. Из треугольника O1O2D3 следует
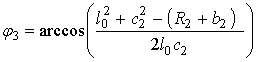 .
.Тогда искомый угол качания рычага O1F или рычага O1D составляет
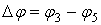 . (4)
. (4)Угол поворота α19 ведущего кривошипа, соответствующий периоду выстоя ползуна между положениями ”1” и ”9”, определяется из анализа рис. 6. Из треугольника O1O2D5 определяется расстояние ld = O2D5
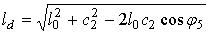 .
.Из условия равенства значений проекций отрезков O1D5 и O2D5 на ось, перпендикулярную линии O1O2, следует 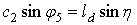 . Отсюда находим
. Отсюда находим
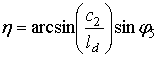 .
.Определяя значение угла γ по формуле (2), находится угол 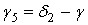 . Из рис. 6 следует, что
. Из рис. 6 следует, что 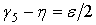 , т. е.
, т. е. 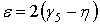 .
.
Тогда находится
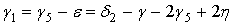 .
.
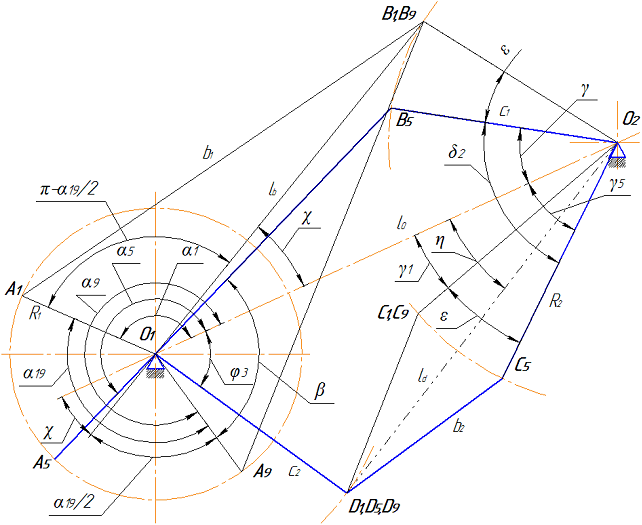
Рис. 6 – Определение угла выстоя ведущего кривошипа
Для положения механизма ”1” находится расстояние lb = O1B1
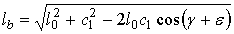 .
.Тогда из треугольника A1O1B1 находим
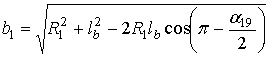 .
.Отсюда следует, что угол α19 есть
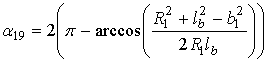 . (5)
. (5)Из треугольника B1O1O2 находится угол χ
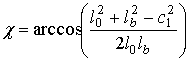 .
.Биссектрисой угла α19 есть прямая O1B1, поэтому угол А1O1B1 равен 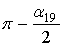 и тогда угол α1, определяющий положение ”1”, будет
и тогда угол α1, определяющий положение ”1”, будет
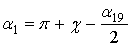 , (6)
, (6)а угол α9, определяющий положение ”9”, будет
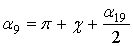 . (7)
. (7)Обращаясь к рис. 5, определим углы α3 и α7. Из треугольника O1B3O2 по теореме косинусов находим угол ζ
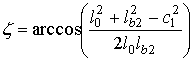 .
.Расстояние lb2 находится по теореме косинусов
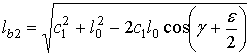 .
.Из треугольника O1A3B3 находим
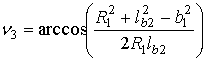 .
.Тогда следует
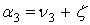 . (8)
. (8)Из треугольника O1A7B3 следует, что 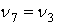 , потому находим
, потому находим
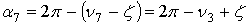 . (9)
. (9)Как указано выше, положения механизма ”2”,”4”,”6” и ”8” соответствуют положению, когда линия перемещения ползуна расположена на биссектрисе угла Δφ. Положение первого четырехзвенника, соответствующее такому условию, когда точки D2, D4, D6, и D8 повернуты относительно точки D3 на угол Δφ/2, показано на рис. 7. Из рисунка следует, что 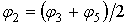 . Из треугольника O1D2O2 расстояние ldn = O2D2
. Из треугольника O1D2O2 расстояние ldn = O2D2
Из треугольника D2С2O2 определяется угол εn
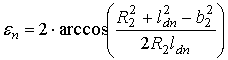 .
.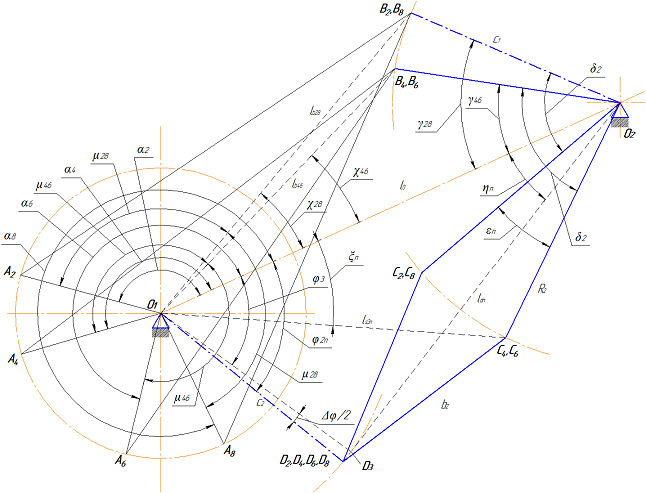 Рис. 7 – Определение промежуточных углов
Рис. 7 – Определение промежуточных угловУгол γ28 определяется как 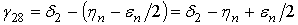 . Угол γ46 определяется как
. Угол γ46 определяется как 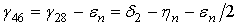 . После определения углов γ28 и γ46 находятся расстояния l28 и l46
. После определения углов γ28 и γ46 находятся расстояния l28 и l46
Из треугольников О1O2B2 и О1O2B4 следует
Из треугольников A2O1B2 и A4O1B4 находим
Таким образом, углы положения ведущего кривошипа, соответствующие положениям ”2”,”4”,”6” и ”8”, будут равны
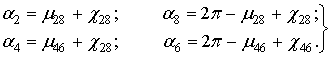 (10)
(10)
Библиографический список
- Артоболевский И.И. Синтез плоских механизмов / И.И. Артоболевский, Н.И. Левитский, С.А. Черкутдинов. – М.: Физматгиз, 1959. – 1084 с.
- Явтушенко А.В. Кинематика многозвенного прижимного механизма механических прессов / А.В. Явтушенко, А.В. Явтушенко, Т.А. Васильченко // Современная техника и технологии. – Март 2014. – № 3 [Электронный ресурс]. URL:http://technology.snauka.ru/2014/03/3324 (дата обращения: 17.03.2014).
Все статьи автора «Явтушенко Александр Викторович»

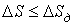 . (1)
. (1) . На рис. 2 показан типовой график движения прижимного Sп и вытяжного Sв ползунов пресса. На рисунке обозначено: αквп, αкнп – соответственно, угол крайнего верхнего и крайнего нижнего положения вытяжного ползуна; αнп, αкп – соответственно угол начала и конца прижима, т. е. выстоя прижимного ползуна; αс – угол выстоя прижимного ползуна после вытяжки; Sp – рабочий ход вытяжного ползуна.
. На рис. 2 показан типовой график движения прижимного Sп и вытяжного Sв ползунов пресса. На рисунке обозначено: αквп, αкнп – соответственно, угол крайнего верхнего и крайнего нижнего положения вытяжного ползуна; αнп, αкп – соответственно угол начала и конца прижима, т. е. выстоя прижимного ползуна; αс – угол выстоя прижимного ползуна после вытяжки; Sp – рабочий ход вытяжного ползуна.

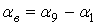 и есть интервал поворота, на котором обеспечивается выполнение условия (1).
и есть интервал поворота, на котором обеспечивается выполнение условия (1).

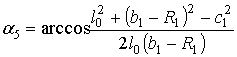 . (2)
. (2) . (3)
. (3)
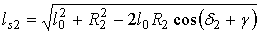 .
.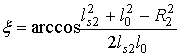 .
.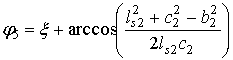 .
.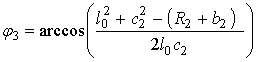 .
.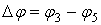 . (4)
. (4)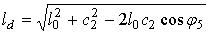 .
.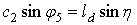 . Отсюда находим
. Отсюда находим
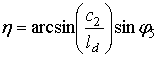 .
.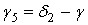 . Из рис. 6 следует, что
. Из рис. 6 следует, что 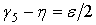 , т. е.
, т. е. 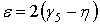 .
. 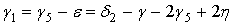 .
.
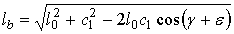 .
.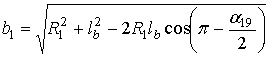 .
.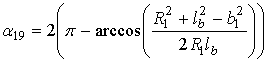 . (5)
. (5)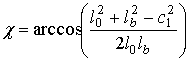 .
.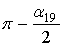 и тогда угол α1, определяющий положение ”1”, будет
и тогда угол α1, определяющий положение ”1”, будет
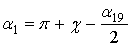 , (6)
, (6)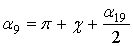 . (7)
. (7)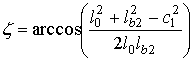 .
.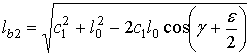 .
.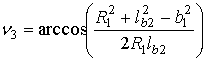 .
.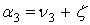 . (8)
. (8)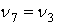 , потому находим
, потому находим
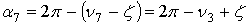 . (9)
. (9)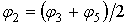 . Из треугольника O1D2O2 расстояние ldn = O2D2
. Из треугольника O1D2O2 расстояние ldn = O2D2
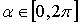
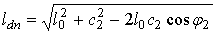
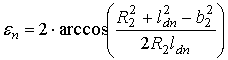 .
.
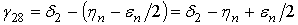 . Угол γ46 определяется как
. Угол γ46 определяется как 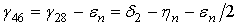 . После определения углов γ28 и γ46 находятся расстояния l28 и l46
. После определения углов γ28 и γ46 находятся расстояния l28 и l46

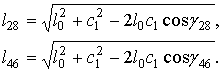
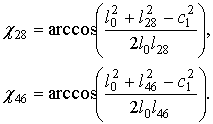
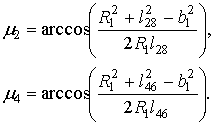
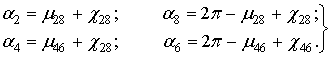 (10)
(10)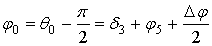 . (11)
. (11)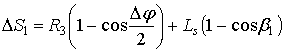 , (12)
, (12)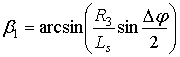 .
.